
- •Тема 4: Теореми Ролля, Лагранжа, Коші, їх геометрична ілюстрація та застосування. Правило Лопіталя.
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 5: Задачі на максимум та мінімум.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Розділ 6. Інтегральне числення функції однієї змінної
- •Тема 1: Невизначений і визначений інтеграл. Властивості інтегралу. Таблиця інтегралів.
- •Короткі теоретичні відомості
- •Властивості невизначених інтегралів:
- •Основні властивості визначеного інтегралу:
- •Література.
- •Тема 2: Інтегрування дробово - раціональних функцій.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 3: Заміна змінної та інтегрування частинами у визначеному інтегралі.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 4:Об’єм тіла обертання.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 5: Площа поверхні обертання.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
- •Тема 6: Довжина дуги кривої.
- •Короткі теоретичні відомості
- •Питання для контролю вивченого матеріалу
- •Література
Тема 4: Теореми Ролля, Лагранжа, Коші, їх геометрична ілюстрація та застосування. Правило Лопіталя.
Теореми Ролля, Лагранжа, Коші, їх геометрична ілюстрація.
Правило Лопіталя.
Короткі теоретичні відомості
Теорема
1.(теорема
Ферма). Якщо функція f
,визначена в деякому околі точки
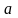 ,
набуває в цій точці найменшого(найбільшого)
в околі значення і має в точці
похідну,
то ця похідна дорівнює нулю.
,
набуває в цій точці найменшого(найбільшого)
в околі значення і має в точці
похідну,
то ця похідна дорівнює нулю.
Теорема 2.(теорема Ролля). Якщо функція f неперервна на відрізку [a;b], диференційована в інтервалі (а;b) й f(a)=f(b),то існує принаймні одна точка є(а;b) така, що f`(c)=0.
Теорема3.(теорема Лагранжа). Якщо функція f неперервна на відрізку [a;b] і диференційована в інтервалі (а;b), то існує принаймні одна точка є (а;b) така, що
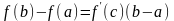 (1)
(1)
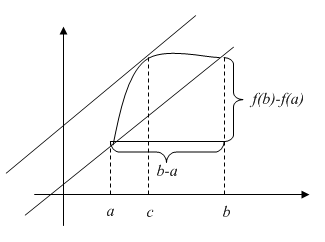
Геометричний зміст теореми Лагранжа полягає в тому, що на дузі, яка є графіком функції f, що задовольняє всі умови теореми Лагранжа, знайдеться принаймні одна точка М(с;f(с)), дотична в якій паралельна хорді. Формула (1) називається формулою Лагранжа, або формулою скінчених приростів.
Теорема
4.(теорема
Коші). Якщо функції
 та
та
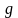 неперервні
на відрізку [a;b]
і диференційовані в інтервалі (а;b),
причому
неперервні
на відрізку [a;b]
і диференційовані в інтервалі (а;b),
причому
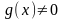 в кожній точці інтервалу (а;b)
, то існує принаймні одна точка є
(а;b)
така, що
в кожній точці інтервалу (а;b)
, то існує принаймні одна точка є
(а;b)
така, що
 (2)
(2)
Формула (2) називається формулою Коші. Теорема Лагранжа є окремим випадком теореми Коші. Щоб дістати формулу Лагранжа з формули Коші , досить покласти g(x)=x.
У формулі (2) зовсім не обов’язково вважати, що b>a.
Наслідком
теореми Коші є правило Лопіталя –
теорема,
яка дає можливість обчислювати границі,
пов’язані з розкриттям невизначеностей
виду
 (перше правило)
(перше правило)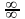 (друге правило). При цьому досить складні
задачі на обчислювання границь зводяться
до більш простих –
обчислення
похідних.
(друге правило). При цьому досить складні
задачі на обчислювання границь зводяться
до більш простих –
обчислення
похідних.
Теорема.
Нехай функції f
і
g
диференційовані проколотому околі
0*(x0)
точки x0
(g`(x)0
xє0*(x0)),
одночасно є нескінченно малим або
нескінченно великим при xx0
(x0R)
або x0=)
і, крім того, існує скінчена або нескінченна
границя відношення
 при
xx0.
при
xx0.
Тоді
існує також і границя відношення
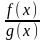 ,
причому
,
причому
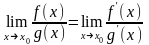 (3)
(3)
Правило
Лопіталя справедливе і для односторонніх
границь. Якщо не існує
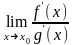 ,
то правило Лопіталя не можна застосовувати
, але шукана границя може існувати.
Правило Лопіталя можна застосовувати
кілька разів.
,
то правило Лопіталя не можна застосовувати
, але шукана границя може існувати.
Правило Лопіталя можна застосовувати
кілька разів.
Приклад
1.
Обчислити границю
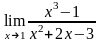 .
.
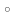 Маємо
невизначеність виду
.
Застосовуючи перше правило Лопіталя
(формула (3)), дістанемо
Маємо
невизначеність виду
.
Застосовуючи перше правило Лопіталя
(формула (3)), дістанемо
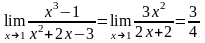 .
.

Приклад
2.Обчислити
границю
 .
.
Маємо
невизначеність виду
.
За другим правилом Лопіталя
 .
.
Приклад
3.Обчислити
границю
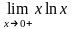 .
.
Маємо
невизначеність
 .
Зведемо її до невизначеності виду
,
записавши вираз у вигляді дробу, а потім
застосовуємо друге правило Лопіталя .
.
Зведемо її до невизначеності виду
,
записавши вираз у вигляді дробу, а потім
застосовуємо друге правило Лопіталя .
Дістаємо
 .
.
Питання для контролю вивченого матеріалу
Сформулюйте теореми Ролля, Лагранжа, Коші.
В чому полягає геометричний зміст теореми Лагранжа?
Сформулюйте правило Лопіталя.
При якій умові правило Лопіталя не можна застосовувати, але шукана границя може існувати?
Обчислити границі:
а)
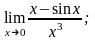

б)
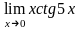 ;
;
в) .
.
Література
Соколенко О.І. Вища математика. -К: Видавничий центр „Академія”,2002-431с.
Дюженкова Л.І, Носаль Т.В. Вища математика: Практикум. -К.: Вища школа, 1991-407с.: іл.
