Продиференціюємо рівняння Пуассона:

,

одержимо

.

(2.7.4)

Підставимо (2.7.4) в (2.7.2):

,

формула (2.7.1) набуде вигляду



(2.7.5)

Використовуючи рівняння Клапейрона-Менделєєва

,

для густини газу маємо:



(2.7.6)

Враховуючи (2.7.5) і (2.7.6), знайдемо, що швидкість звуку в газі визначається формулою



(2.7.7)

де Т – температура повітря; R – універсальна газова стала ; – молярна маса газу (для повітря ); – показник адіабати.

Виразимо як



(2.7.8)

Таким чином, для визначення коефіцієнта Пуассона досить виміряти температуру газу і швидкість розповсюдження звуку.

Опис вимірювальної установки і методика вимірювань

Д ля вимірювання швидкості звуку використовують установку, зображену на рисунку 2.7.1.

Звукові коливання в трубі збуджуються телефоном Т. Коливання сприймаються мікрофоном М. Мембрана телефону приводиться в рух змінним струмом звукової частоти. Як джерело змінної ЕРС використовується звуковий генератор ЗГ. Сигнал, що виникає в мікрофоні, спостерігається на осцилографі ЕО.

Звукова хвиля, що розповсюджується уздовж труби, багаторазово відбивається від торців.

Якщо довжина труби L рівна цілому числу півхвиль, тобто



(2.7.9)

де – довжина звукової хвилі в трубі; n – будь-яке ціле число, то падаючі і відбиті хвилі збігаються за фазою і підсилюють одна одну. Амплітуда звукових коливань при цьому різко зростає – наступає резонанс.

За постійної довжини труби можна змінювати частоту звуку. Плавно змінюючи частоту звукового генератора , а також довжину звукової хвилі , спостерігатимемо на осцилографі виникнення резонансу за різким зростанням амплітуди коливань.

Для послідовних резонансів маємо:

    .

(2.7.10)

Швидкість звуку пов’язана з його частотою і довжиною хвилі співвідношенням



(2.7.11)

З (2.7.10) і (2.7.11) маємо

,

де n – “номер резонансу” в першому досліді за найменшої частоти; , 1, 2, 3, 4 (якщо 5 дослідів).

Порядок виконання роботи

Таблиця 2.7.1

№ п/п	, Гц	, Гц	, м/с
; м

Таблиця 2.7.2

, м/с

, К

, %

– експериментальне значення що розраховується за формулою (2.7.8)

– теоретичне значення що розраховується за формулою (2.7.8) з врахуванням того що швидкість звуку в повітрі для К

– відносна похибка (2.7.12)

Додаток Механічні (пружні) хвилі

Хвилями називаються всілякі збурення стану речовини або поля, що розповсюджуються в просторі з часом.

Пружні хвилі – механічні збурення, які розповсюджуються в пружному середовищі.

Середовище вважається пружним, коли між його частинками існують сили взаємодії, що перешкоджають деформації цього середовища.

Якщо тіло коливається в пружному середовищі, то воно впливає на частинки середовища, прилеглі до нього, і примушує їх здійснювати вимушені коливання. Середовище поблизу тіла, що коливається, деформується, в ньому виникають пружні сили. Ці сили діють на все більш віддалені від тіла частинки середовища, виводячи їх з положення рівноваги. У просторі розповсюджується хвиля.

Поперечні і поздовжні хвилі

Хвиля називається поперечною, якщо частинки середовища коливаються в напрямках, перпендикулярних до напрямку розповсюдження хвилі.

Модель поперечної хвилі

Уявимо собі ланцюжок, що складається із рівновіддалених одна від одної матеріальних точок, які зв’язані пружинками.

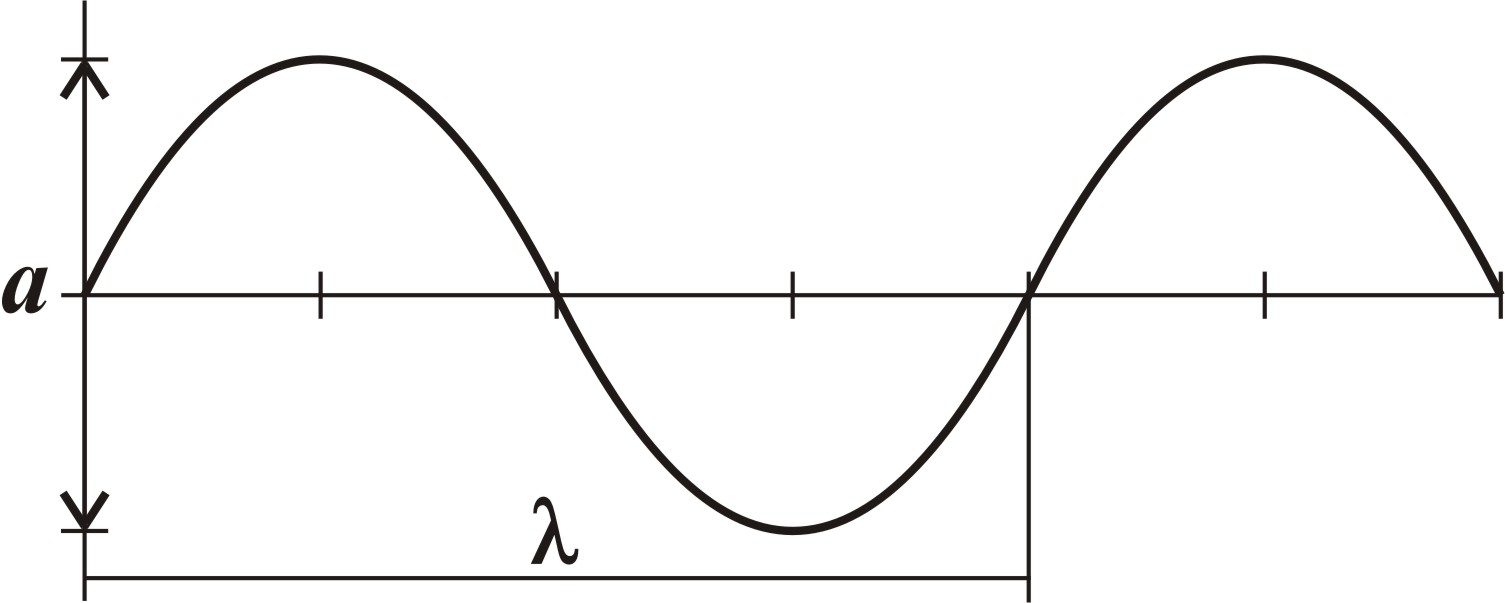Я кщо ми приведемо яку-небудь точку “а” в коливальний рух в напрямі, перпендикулярному до лінії ланцюжка, то й інші точки послідовно включаться в коливальний процес. Всі частинки здійснюватимуть коливання, тотожні з точкою “а”, але не одночасно, а поступово запізнюючись за фазою. Виникне поперечна хвиля.

Хвиля називається поздовжньою, якщо коливання частинок середовища відбуваються у напрямі розповсюдження хвилі.