1.3 Фрактальная размерность
Зависимость измеренной длины береговой линии от длины шага [км] - длины стороны квадратных ячеек, образующих покрытие береговой линии на карте оказалось удобным изобразить в дважды логарифмическом масштабе, т.е. log(L() [км]) = f(log()[км]).
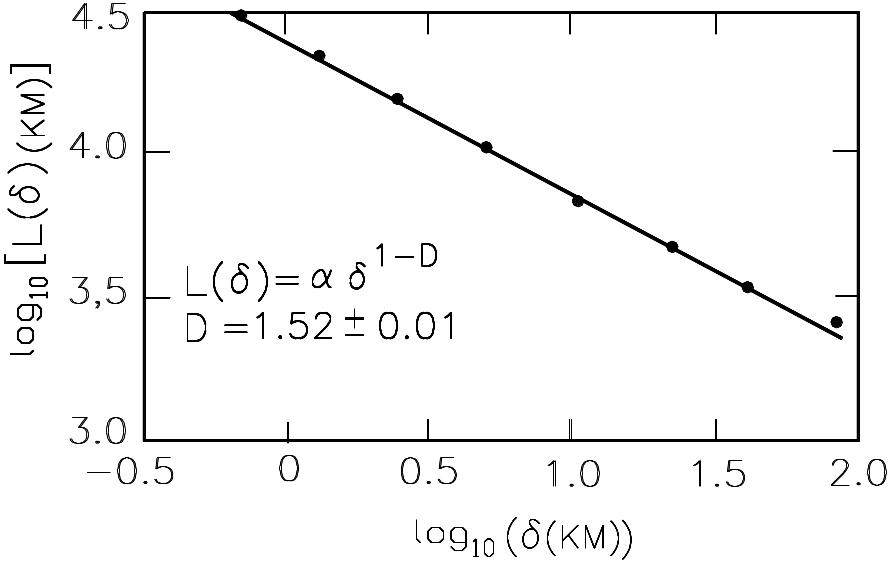
Рисунок 1.2. - Измеренная длина береговой линии, изображенной на рисунке 1, как функция шага (км) - длины стороны квадратных ячеек, образующих покрытие береговой линии на карте.
Как видно из рисунка 1.2 при уменьшении длины шага измеренная длина отнюдь не стремится к постоянному значению, а возрастает. При этом она прекрасно описывается приближенной формулой
L() = a 1-D . (1.1)
Для обычной кривой можно было бы ожидать, что a = LN (по крайней мере при достаточно малых ), и показатель D равен единице. Но для береговой линии Норвегии, как видно из графика, D 1.52. Для береговой линии Великобритании, как оказалось, показатель D 1.3. Говорят, что береговая линия - это фрактал, или фрактальная кривая. На рисунке 1.3 подобные зависимости приведены для разных побережий.
Мы видим, что для фрактальной кривой длина не является характерной величиной. При уменьшении она стремится к бесконечности. Площадь также не пригодна для оценки таких кривых, так как для плоской кривой в пространстве она равна нулю.
Понятия “длина”, “площадь”, “объем” связаны с понятием размерности. Так, для кривой размерность D = 1, для плоской фигуры D = 2 и т.д. И нет смысла применять к геометрическому объекту понятие несвойственной ему размерности. Таким образом, мы имеем для кривой, геометрической фигуры, геометрического тела дискретный ряд целочисленных значений, определяющих их топологическую размерность: 1, 2, 3. Фракталы как бы “не вписываются” в этот ряд. Они тоже должны иметь свою размерность, но поскольку между 1 и 2 нет промежуточных целых значений, “размерность” фрактальной кривой должна быть дробной. В качестве такой дробной размерности и принят показатель степени D в формуле (1). Таким образом, мы можем сказать, что береговая линия Норвегии - это фрактал с фрактальной размерностью D = 1.52, а береговая линия Великобритании - фрактал с размерностью D = 1.3. Именно отсюда и происходит название “фрактал” (по английски слово FRACTionAL означает “дробный”).
1.4 Фрактальные кластеры.
Если мы перейдем к рассмотрению реальных физических систем, то увидим, что они в отличие от математических, где мы можем устремлять величину d к нулю, обладают характерным минимальным линейным размером, таким, как радиус атома или молекулы. Однако и здесь мы встречаемся с объектами, которые, несомненно имеют фрактальную структуру. Характерным примером таких объектов служит так называемый фрактальный кластер, или фрактальный агрегат. Это система, которая имеет рыхлую, ветвистую структуру и образуется в большом наборе физических процессов, сопровождающихся ассоциацией твердых частиц близких размеров. Эти процессы, в частности, происходят при образовании гелей в растворах, при слипании частиц в дымах. Характерным свойством фрактального кластера является то, что по мере его роста плотность вещества в объеме, занимаемом кластером, падает.
Фрактальные агрегаты (кластеры) являются ярким примером процессов самоорганизации в неживой природе.
Фрактальный кластер состоит как бы из набора “склеенных” частиц, размеры которых значительно меньше размера кластера. Само слово “кластер” ( от английского cluster - гвоздь) употребляется для системы большого числа связанных атомов и молекул, но в последнее время этот термин распространяется также и на системы, состоящие из большого числа связанных макроскопических частиц.
Рост фрактального кластера можно имитировать на ЭВМ. Одной из наиболее распространенных моделей роста кластеров является так называемая модель ограниченной диффузией агрегации (ОДА). В этом процессе частицы поступают из удаленного источника и диффундируют, совершая случайные блуждания. Достигнув кластера (первоначально - центра кристаллизации), частицы прилипают к нему, образуя ветвистую структуру. Это и составляет содержание лабораторной работы, котрую вы будете выполнять.
В процессе выполнения лабораторной работы вы построите фрактальный кластера с помощью компьютерной программы.
1.5
Порядок выполнения работы:
1) Запустите на выполнение программу построения кластера klar.exe или klar1.exe.
Внимание! В десятичных
дробях после нуля следует ставить
точку!
Хранитель экрана должен
быть выключен.
Следите за числами-индикаторами
в нижнем правом углу экрана:
первая строчка – текущее
число частиц в кластере;
вторая строчка – радиус
растущего кластера; кластер
считается полностью построенным, когда
значение радиуса достигнет 50;
при этом вы услышите мелодию – это
сигнал окончания построения;
третья строчка – фрактальная
размерность FD
– ее надо занести в таблицу 1 по окончании
построения.
Примечание:
в некоторых случаях происходит
«прилипание» частиц к надписи, радиус,
таким образом, резко увеличивается и
звучит мелодия окончания построения.
В этом случае надо нажать клавишу ввод
и продолжить построение. Скорость
построения кластера зависит от заданной
скорости v
и быстродействия компьютера.
3) понаблюдайте за ростом кластера и изменением его фрактальной размерности;
4) запишите окончательное значение фрактальной размерности;
5) повторите моделирование для значений параметров больших и меньших первоначального, занося результаты в таблицу 1.
Таблица 1.
Значения параметра скорости v |
|
|
|
|
Фрактальная размерность D |
|
|
|
|
6) постройте график FD = f(v) , где v - скорость.
FD
v
7) сделайте вывод о связи между параметром скорости видом кластера и его фрактальной размерностью.