Лекция 5 Поляризация электромагнитных волн

Выше было показано, что вектора ноля и электромаг­нитной волны в изотропной среде ориентированы друг относи­тельно друга под прямым углом и лежат в плоскости, перпенди­кулярной направлению распространения волны. Их ориентация и поведение в пространстве могут быть различными и определя­ются поляризационной характеристикой электромагнитной волны.

Для описания поляризационной характеристики поля вводят понятие плоскости поляризации электромагнитной волны. За эту плоскость условно принята плоскость, проходящая через на­правление векторов и . Вектор называют вектором поляризации. Классификацию электромагнитного поля по поляри­зационным характеристикам проводят следующим образом. Разли­чают:

1. Поле линейной поляризации или линейно - поляризованную волну. Такая волна характеризуется постоянным положением пло­скости поляризации: В зависимости от ориентации этой плоскос­ти относительно выбранной системы координат линейную поляри­зацию подразделяют: на вертикальную, горизонтальную и на­клонную.

2. Поле круговой поляризации - это поле, для которого плоскость поляризации вращается вокруг оси распростране­ния волны с круговой частотой сигнала, а вектор при этом описывает своим концом окружность. Различают круговую поляри­зацию правого и левого вращения.

3. Наиболее общий случай - поле эллиптической поляри­зации.

Поле любой поляризации может быть получено в результате суперпозиции двух полей со взаимно ортогональной линейной поляризацией.

Запишем электрическую составляющую двух линейно поляри­зованных волн с ортогональными векторами поляризации:

(40)

В зависимости от отношения амплитуд и фаз и суперпозиция этих полей дает любой из названных видов поля­ризации. Так, полю линейной поляризации соответствует в (40) разность фаз где При этом тангенс угла наклона плоскости поляризации . Круговая поляризация получится, если , а .

Для тангенса угла наклона плоскости поляризации , т.е. угол наклона плоскости поля­ризации изменяется с частотой , а амплитуда вектора ре­зультирующего поля будет постоянной:

Таким образом, конец вектора Е в процессе распространения описывает окружность. Направление вращения определяется зна­ком перед углом , и зависит от значения . Любое другое отношение амплитуд и фаз двух исходных полей дает поле эл­липтической поляризации.

Условие прохождения и отражения волн на границе раздела двух сред

Электромагнитная волна, падающая на границу раздела двух сред под углом , делится на волну, отраженную от границы под углом , характеризующиеся коэффициентом отражения , и волну, прошедшую через границу под углом , характеризую­щуюся коэффициентом передачи . Лучи или направление рас­пространения падающей, отраженной и прошедшей волны лежат в плоскости падения, ортогональной плоскости раздела сред (рис. 3). Соотношения между углами , и и коэффициента­ми и получаются из граничных условий для векторов поля электромагнитной волны на границе раздела двух сред. Значения этих коэффициентов и углов зависят от параметров двух сред и ориентации векторов поляризации относительно плоскости паде­ния волны.

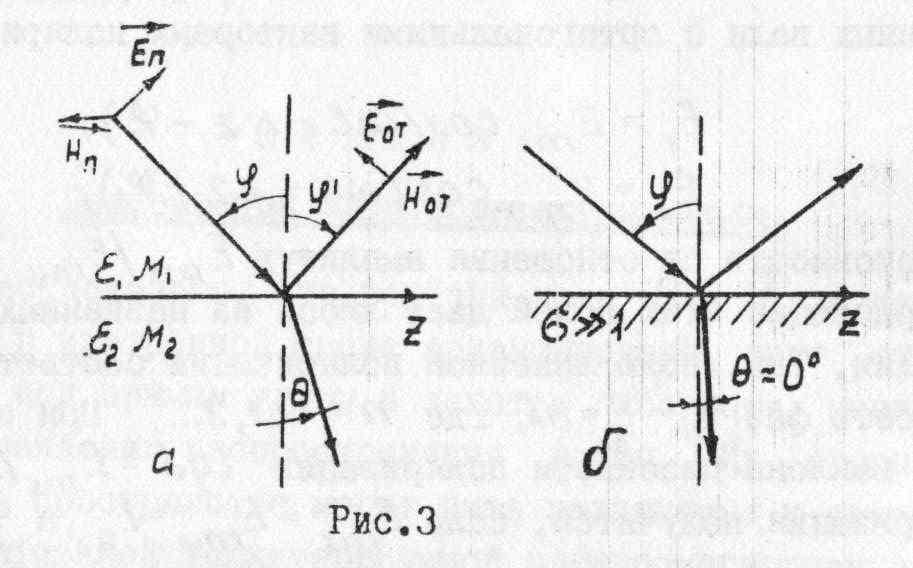
Рассматривают два случая:

1. случай параллельной поля­ризации , когда вектор поляризации лежит в плоскости па­дения волны;

2. случай нормальной поляризации , когда век­тор поляризации ортогонален плоскости падения и параллелен границе раздела двух сред.

Падение плоской волны на границу раздела двух диэлект­риков. Имеется две среды с общей плоской границей. Параметры сред равны и , постоянные распространения - и ,и волновые сопротивления - и . В первой среде под углом к границе (рис. 3) падает плоская волна с амплитудой . Связь между направлениями распространения отраженной и прошедшей волн дают законы Снеллиуса:

1) угол падения равен углу отражения ;

2) отношение синуса угла падения и прохождения равно от­носительному показателю преломления сред

Амплитудные соотношения между отраженной и прошедшей вол­ной зависят от поляризации волны и характеризуются коэффициен­том отражения и коэффициентом прохождения , которые так­же называются коэффициентами Френеля.

Для случая параллельной поляризации

(41)

Для нормально поляризованной волны

(42)

При нормальном падении волны

;

Если вторая среда - идеальный проводник ,и

то на основании (41) и (42) ; ; , т.е. от идеальнопроводящей поверхности происходит полное отраже­ние электромагнитной волны.

Падение плоской волны на границу поглощающей среды. Рас­смотрим случай, когда вторая среда обладает большими потеря­ми, т.е. , , тогда .Из вто­рого закона Снеллиуса для этого случая следует:

; (43)

Так как величина , то , и угол преломления независимо от угла падения всегда близок к нулю: . Таким образом, волна, падающая на границу реального провод­ника, проникает в него под прямым углом; независимо от угла падения .