Волноводы круглого сечения

Геометрия поперечного сечения круглого волновода пока­зана на рис. 12. Решение волнового уравнения для этих волно­водов проводят в цилиндрической системе координат с перемен­ными и при граничных условиях на стенках , Для электрических и магнитных волн решение этого уравнения име­ет вид

(65)

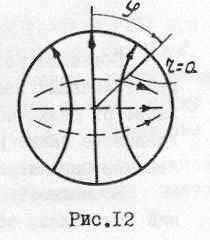г де - функция Бесселя первого рода т-го порядка аргумента , изменяется . Значение попереч­ного волнового числа находим из гра­ничных условий. Для волн типа Е и из (65) следует, что т.е. аргумент функция Бесселя при должен соответство­вать n-му корню и значит:

;

Здесь т характеризует число полных периодов изменения по­ля по координате ; ; п - изменение поля вдоль радиуса или число полюсов функции . Значения поперечного волнового числа и определяются n-м корнем функции Бесселя m -го порядка и зависят от радиуса волново­да a. Для магнитных типов волн значение поперечного волно­вого числа находится из следующих граничных условий для продольной составляющей магнитного поля:

На основании этого уравнения из решения (65) получим уравне­ние для определения поперечного волнового числа .

Таким образом, поперечное волновое число находится как п-й корень производной функции Бесселя первого рода m-го порядка:

;

Для круглого волновода основной волной является волна H₁₁ , а ее ближайший высший тип - волна Е₀₁ :

;

Для Е и Н типов волн в круглом волноводе индекс т может принимать значение нуль, а n - всегда больше нуля. Структу­ра поля волны H₁₁ показана на рис. 12.

Лекция 9 Объемные резонаторы

Объемные резонаторы относятся к одним из наиболее рас­пространенных избирательных элементов СВЧ диапазона. В от­личие от низкочастотных избирательных LC -контуров в СВЧ диапазоне такие устройства реализуются в системах с распреде­ленными параметрами.

Возможность построения таких систем вытекает из уравне­ний Максвелла, согласно которым изменение электрического поля вызывает появление магнитного поля . Такой обмен энергиями этих полей происходит в любой точке пространст­ва. Из уравнения энергетического баланса (26), (27) следует, что если в замкнутой области отсутствуют тепловые потери, по­тери на излучение, то этот обмен может происходить сколь угодно долго. Поэтому свойствами колебательной системы обла­дает любая изолированная система, ограниченная отражающей оболочкой. Основными параметрами резонаторов на СВЧ, в отли­чие от колебательных контуров с сосредоточенными параметрами, которые характеризуются L , С , R , являются:

1) резонансная длина волны , или частота f_o ;

2) активная проводимость - мера активных потерь;

3) собственная или ненагруженная добротность .

Параметры , , полностью описывают характе­ристики резонаторов на СВЧ.

Резонансная длина волны. Рассмотрим условие существова­ния электромагнитного поля в отрезке регулярной направляющей системы длиной , з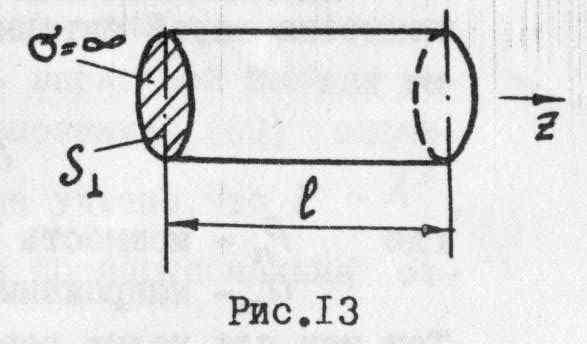 акороченной по концам при и иде­ально проводящей металлической стенкой (рис. 13). Граничное условие (25) для поперечной составляющей электрического поля на стенках будет при , . С учетом этого условия электро­магнитное поле в такой системе может существовать только в виде суперпозиции двух встречных волн одинаковой амплитуды, т.е. для электрического поля можно написать

(66)

Отсюда из (66) на основании граничных условий (25) при получим, что , а условие при дает , т.е. . Значит, длина замкнутой направляющей системы должна быть кратной целому числу длин полуволн где . Выражение (66) показывает, что фаза поля в колебательной системе неизменна и поле носит характер стоячей волны. Резонансная частота и резонансная длина волны для резонатора длиной может быть

определена следующим образом:

;

Очевидно, на основании (I) для волн типов Т и Н , у кото­рых полное электрическое поле , значение нуль при­нимать не может. Для волн типа Е равенство нулю означа­ет, что полное электрическое поле , а длина резонатора при является неопределенной.

Тип волны в резонаторе обозначается тремя индексами : т, n, p. Первые два определяют структуру поля в поперечном сечении, третий - характеризует поле стоячей волны в про­дольном сечении резонатора, например: ; .

Активная проводимость резонатора. Эта характеристика является мерой активных потерь в резонаторе и ее определя­ют как

где Р_п - мощность активных потерь в резонаторе;

U_m- напряжение на входных клеммах резонатора.

Так как для полых резонаторов нет однозначного определения величины напряжения U_m , то понятие G является неопреде­ленным. Обычно U_m определяют как между характерными точками резонатора ( а и b), например, на входных клеммах. Если допустить, что потери в резонаторе имеют место только в металлических стенках с поверхностным сопротивлением , то величину потерь в резонаторе можно оценить следующим образом:

(67)

Из выражения (67) следует, что мощность активных потерь и, следовательно, активная проводимость резонатора зависит от качества материала, его обработки и от структуры поля.

Добротность резонатора. Для определения добротности ре­зонаторов используют известное энергетическое соотношение для средних за период величин:

где - резонансная частота;

Т_к - период колебания;

- запасенная электромагнитная энергия.

В момент фазы колебания, когда , запасенная энер­гия может быть подсчитана:

(68)

Значение собственной добротности с учетом (67) и (68) будет

(69)

где в выражениях (67) и (68) учтено, что для немагнитных материалов . Если пренебречь вариацией поля в ре­зонаторе и полагать, что , то выражение (69) значительно упростится: , где учтено, что , , т.е. добротность резонатора пропорциональна от­ношению .

При заполнении объемного резонатора диэлектриком с по­терями мощность потерь в диэлектрике определяет­ся:

а запасенная энергия . Добротность в диэлектрике будет , а при наличии магнитных потерь .

На практике часто используют выражение добротности ре­зонатора через значение активной и реактивной проводимости G, В на его входных клеммах. Для этого по аналогии с контурами запасенную энергию, мощность потерь в резонаторе и его добротность представляют как

; ; (70)

Значение емкости С для систем с распределенными параметра­ми однозначно не определяется, поэтому ее выражают через входную реактивную проводимость b . Полная входная реактив­ная проводимость для контуров вблизи резонанса имеет вид:

где учтено, что . Вблизи резонанса при , и выражение для реактивной проводимости b будет , откуда . Отсюда выражение (70) для добротности может быть записано как

(71)

Соотношение (71) характеризует добротность резонатора вблизи резонансной частоты.

Нагруженная и внешняя добротность резонатора. Если ре­зонатор подключен к полезной нагрузке, то полная энергия по­терь будет , а добротность резонатора с нагрузкой характеризуется нагруженной добротностью

где - внешняя добротность резонатора - определяется, ве­личиной нагрузки

Соответственно величина добротности через эквивалентные про­водимости по аналогии с (71) примет вид:

Нагруженная добротность зависит от величины связи резонатора с нагрузкой и от его собственной добротности.