Глава 2 Циклические Ускорители с постоянным во времени магнитным полем

Как было ранее установлено, энергия частиц ускорителей прямого действия ограничена. Предельная величина электрического напряжения, которое может быть получено на таком ускорителе, определяется электрической прочностью трубки и ряда изолирующих промежутков. Считается целесообразным не повышать это предельное напряжение свыше (5…6)∙10⁶ в. Даль­нейшее повышение напряжения связано с большими техническими трудностями и чрезмерными затратами. Применение ускорите­лей сдвоенного типа позволяет увеличить энергию частиц в два и три раза. Однако при этом резко снижается интенсивность пучка ускоренных частиц.

Поворот пучка и ускорение частиц в циклическом ускорителе

Физика требует от ускорительной техники создания машин на значительно большие энергии, чем 10…15 Мэв. Одним из са­мых удобных способов разгона заряженных частиц до больших энергий, при ограниченном напряжении в пространстве, где про­исходит ускорение, является многократное прохождение одних и тех же частиц через это пространство. Такой принцип положен в основу действия так называемых циклических ускорителей. В ускорителях частицы движутся по некоторой криволинейной траектории, обеспечивающей многократное прохождение частиц через один или несколько ускоряющих промежутков. Может возникнуть мысль о том, что возможно, искривив траекторию движения частиц, многократно пропустить их через ускоряю­щую трубку ускорителя прямого действия так, как показано на рис. 34. Однако такая схема не дает нужного эффекта.

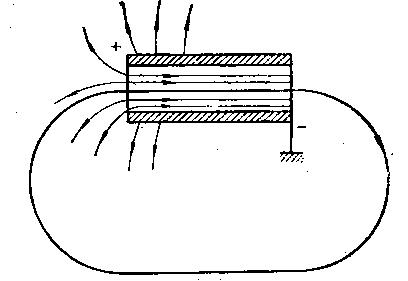
Рис.34. Схема электрического поля ускорительной трубки при многократном

про­пускании через нее частицы

Частицы, вышедшие из прямого заземленного конца трубки и вернувшиеся в трубку слева, встретят при подходе к трубке электрическое поле, направленное в сторону, обратную направлению движения частиц. Не дойдя до левого отверстия трубки, они потеряют всю свою энергию, приобретенную внутри трубки при первом цикле ускорения.

Такая схема, следовательно, непригодна для использования в циклических ускорителях. Необходимо, чтобы внешнее поле отсутствовало.

Одна из возможных схем ускоряющего устройства представ­лена на рис. 35.

Здесь А и В — две ускоряющие трубки, соединенные последовательно, С — металлическая про­водящая трубка необходи­мой длины. Правый и ле­вый концы трубок зазем­лены. Таким образом, при подходе к трубке частица не встречает никакого электрического поля. В верхней части рисунка показан момент, когда ча­стица вошла в трубку А. Металлическая трубка С имеет отрицательный по­тенциал. Электрическое поле направлено в сторону движения частицы, и частица ускоряется.

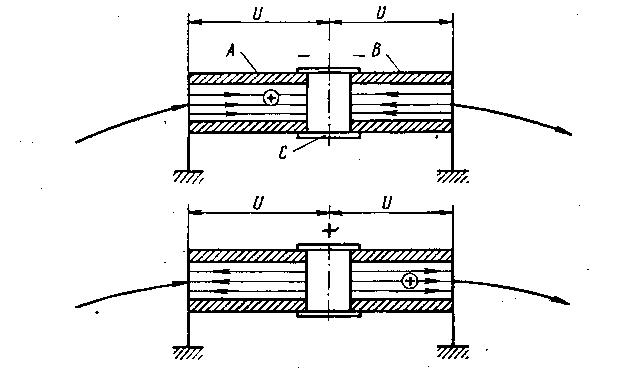
Рис. 35. Схема, при которой возможно ускорение частицы, многократно проходящей через ускорительное устройство

При постоянном значении напряжения U частица, пройдя промежуток С и войдя в трубку В, встретит поле, направленное влево, и будет тормозиться. Дойдя до правого конца трубки В, она полностью потеряет всю ту энергию, которую она накопила в трубке А. Поэтому нужно, чтобы за то время, в течение которого частица находится внутри металлической трубки С, в пространстве, лишенном электрического поля, потенциал трубки С сменил знак на обратный, при этом трубка С получила бы положительный заряд, и частица, войдя в ускорительную трубку В, была бы вновь ускорена (см. рис. 35 внизу). При многократном прохождении частицы через ускоряющие устройства нет необходимости иметь очень большое электрическое напряжение порядка миллионов вольт. Многократно проходя через это устройство даже при сравнительно низком напряжении — порядка нескольких киловольт, частица может набрать нужную энергию. Поэтому, нет надобности, выполнять ускоряющие устройства в виде сложных трубок с фарфоровыми кольцами и электродами, как делается в ускорителях прямого действия.

Еще более простое ускоряющее устройство схематически показано на рис. 36.

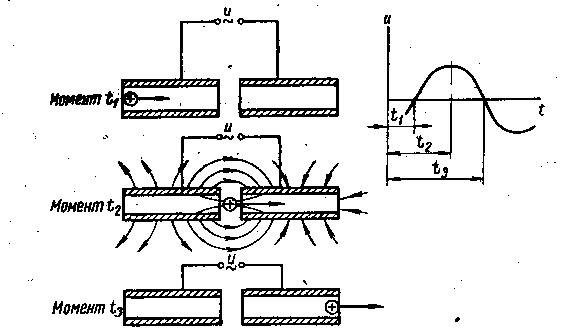
Рис. 36. Простейшее ускорительное устройство с питанием его переменным электрическим напряжением

Оно состоит из двух металлических проводящих трубок, присоединенных к источнику переменного напряжения U. Частица, пришедшая к ускоряющему устройству слева в момент t₁ когда мгновенное значение U равно нулю, беспрепятственно войдет в левую трубку. В течение времени, пока частица движется в левой трубке в пространстве без электрического поля напряжение растет, и в момент t₂ при максимальном или близким к нему значении напряжения частица пройдет пространство между двумя трубками, в котором имеется электрическое поле. Пройдя этот промежуток, частица получит прирост энергии в электронвольтах, численно равный напряжению, соответствующему моменту t₂. Частица должна выходить из правой трубки в момент t₃, когда напряжение равно нулю и никакого тормозящего поля вблизи трубки нет.

На рис. 35 и 36 приведены схемы двух возможных вариантов ускорения при многократном прохождении частицы через ускоряющее устройство. Эти варианты не исчерпывают всех воз­можных схем ускоряющих устройств. Однако все они должны обязательно работать при переменном электрическом напряжении и, очевидно, при весьма высокой частоте, определяемой разме­рами ускоряющих устройств и большой скоростью прохождения частиц через эти устройства.

Второй особенностью циклических ускорителей являются кри­волинейные траектории движения частиц, обеспечивающие воз­врат их к ускоряющим устройствам. Для получения криволи­нейной траектории необходимо наличие силы, действующей на частицу в направлении, перпендикулярном к касательной к траек­тории. Существуют три вида сил, которые могут воздействовать на движущуюся частицу и обеспечить криволинейность траек­тории ее движения. Это гравитационные силы, силы, создаваемые электрическим полем, и силы, вызванные взаимодействием дви­жущейся частицы с магнитным полем.

Гравитационные силы должны быть сразу отвергнуты как непригодные для воздействия на заряженную частицу. Известно, что уже при cкорости свыше 11,2 км/с движущееся тело покидает пределы Земли. Скорости, с которыми имеют дело в ускори­телях, на много порядков больше, чем эта так называемая косми­ческая скорость. Гравитационные силы весьма малы, чтобы их можно было использовать для создания криволинейных траекто­рий в циклическом ускорителе.

Силы электрического поля, в принципе, могут быть использованы для осу­ществления замкнутых криволинейных траекторий.

Очевидно, реально осуществимое значение электрического поля может быть порядка 50 кв/см. При этом значении электрического поля для протонов при малых энергиях радиус круговой траектории для протонов с энергией порядка 10 ГэВ составит около 2 км.

Есть и второе обстоятельство, препятствующее использова­нию электрического поля. Пространство, в котором движутся частицы в циклическом уско­рителе, должно иметь достаточный объем. Частицы, двигаясь вдоль вакуумной камеры, совершают колебания в радиальном направлении. Чтобы при этом частица не потерялась на стенках ка­меры, радиальный размер ее должен быть значитель­ным — порядка нескольких десятков сантиметров. При напряженности электриче­ского поля, принятой нами в этом примерном расчете, Е = 50 кв/см и при расстоя­нии между электродом 10 см нужно иметь весьма большое напряжение U = 500 кв.

На рис. 37 схематически показана возможная система цикли­ческого ускорителя с электрическим полем.

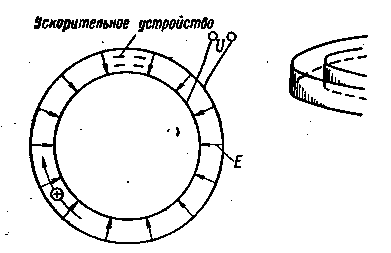
Рис. 37. Система цикли­ческого ускорителя с электрическим полем

Здесь движение частицы происходит по кольцевой траектории между двумя обкладками цилиндрического конденсатора. Электрическое поле с напряженностью Е направлено радиально. В одной или не­скольких точках этой траектории размещено ускоряющее устрой­ство, выполненное по одной из ранее рассмотренных схем.

Из-за необходимости применять очень высокое напряжение и вследствие больших размеров сооружения электростатический способ отклонения частиц в циклических ускорителях не исполь­зуется. Он находит применение лишь в некоторых вспомогатель­ных устройствах таких ускорителей.

Частица в постоянном магнит­ном поле движется по круговой траектории. Для нашего примера радиус кривизны траектории при магнитном отклонении частицы почти в 100 раз меньше, чем при электростатическом. Электромагнитный метод отклонения частицы является наилучшим из возможных и используется во всех циклических ускорителях.

Частица с неизменной энергией w в постоянном магнитном поле, вектор напряженности которого, перпендикулярен плоскости орбиты, движется по круговой траектории. Здесь центробежная сила

уравновешивается силой Лоренца

.

Если магнитное поле равномерное, а скорость частицы постоянна (постоянная энергия w), то лоренцева сила будет постоянной и не зависящей от радиуса орбиты. Центробежная сила обратно пропорциональна радиусу кривизны траектории. При постоянной массе частицы и постоянной скорости ее вращения, мы будем иметь гиперболическую зависимость центробежной силы от радиуса (кривая Р_с на рис. 38а).

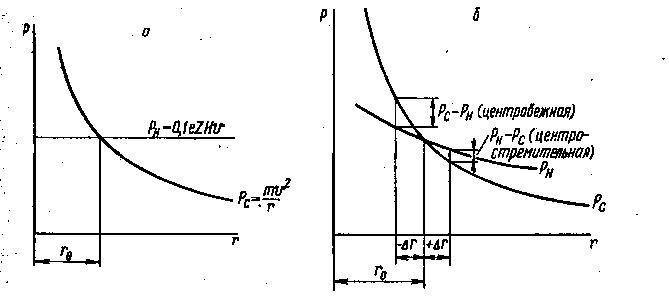
Рис. 38. Зависимость центробежной силы и силы Лоренца от радиуса вращения частицы в магнитном поле при равномерном а и подающем б магнитном поле

В действительности в ускорителях напряженность магнитного поля не остается постоянной при различных радиусах, а несколько падает с увеличением радиуса. Поэтому кривые лоренцевой силы и центробежной силы в зависимости от радиуса будут выглядеть так, как показано на рис. 38б.

Из рис. 38 видно, что равенство двух противоположно на­правленных сил имеет место только при каком-то определенном значении радиуса r₀. При всех других значениях силы не равны. Радиус, соответствующий точке равенства сил, носит название радиуса равновесной орбиты. Во всех точках этой орбиты соблю­дается условие равновесия двух сил и частица при случайном отклонении ее траектории от равновесной орбиты стремится воз­вратиться обратно на эту орбиту. Так, при переходе на орбиту большего радиуса, равного г₀ + Δr, (см. рис. 38) лоренцева сила станет большей, чем центробежная, и на частицу будет дей­ствовать суммарная центростремительная сила

.

При отклонении частицы от равновесной орбиты в сторону меньшего, радиуса г₀ - Δr центробежная сила станет большей, чем центростремительная сила Лоренца, и суммарная сила бу­дет центробежной. Таким образом, всякое изменение радиуса траектории частицы приведет к появлению силы, стремящейся возвратить частицу на равновесную орбиту. Сила, возвращающая частицу на равновесную орбиту, возрастает с увеличением Δr. Это создает устойчивость ее движения в радиальном направлении.

Так как частицы в ускорителях движутся в вакууме, то тре­ние, препятствующее их движению (если пренебречь излучением для электронов), отсутствует, и частицы совершают гармониче­ские колебания около равновесной орбиты (рис. 39).

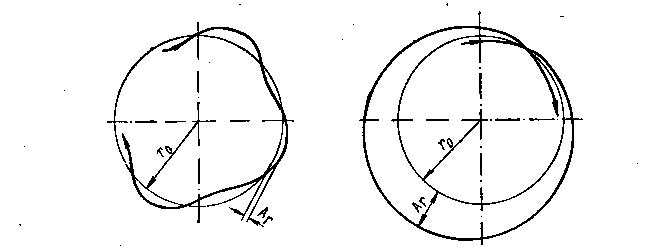
Рис. 39. Радиальные свободные колебания частицы вокруг круговой равновесной орбиты

Амплитуда радиальных колебаний Δr зависит от величины силы, отклонив­шей частицу от равновесной орбиты. При большом количестве частиц каждая из них совершает колебания независимо от других, поэтому вокруг равновесной орбиты появится целая область, в которой будут находиться частицы.

Таким образом, движение частицы в равномерном (однород­ном) магнитном поле будет устойчивым в радиальном направле­нии. При равномерном магнитом поле частицы могут свободно перемещаться вдоль силовых линий магнитного поля до тех пор, пока не соприкоснутся с поверхностью полюса магнита и не выпадут из режима ускорения. Силы, которые заставят частицу двигаться вертикально вдоль силовой линии магнитного поля, могут быть различными. Это тепловые скорости частицы, случайное возмущение, например, столкновения с молекулами газа, некоторая начальная неперпендикулярность вектора скорости частицы к вектору напряженности магнитного поля и, наконец, сила тяжести. При достаточно продолжительном пребывании частицы на орбите она просто упадет на нижний полюс магнита. Поэтому для обеспечения вертикальной устойчивости нужно принять специальные меры. Во всех циклических ускорителях вертикальная устойчивость обеспечивается способом, схематически показанным на рис. 40.

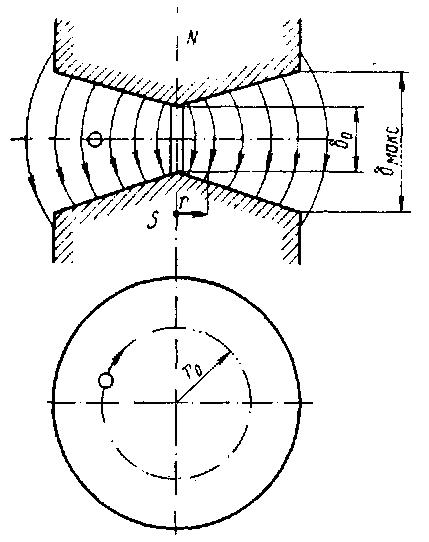
Рис. 40. Схема электромагнита с падающей по радиусу напряжен­ностью магнитного поля для обес­печения вертикальной устойчиво­сти частицы

Зазор магнита, в котором происходит ускорение частиц, растет с увеличением радиуса. Напряженность магнитного поля Н при этом падает, и силовые линии поля оказываются искривленными, бочкообразными. Плоскость орбиты частицы совпадает со средней плоскостью зазора магнита, и всякое отклонение частицы в вертикальном направлении и отход ее от средней плоскости приводит к появлению вертикальной фокусирующей силы, т. е. силы, которая возвращает частицу обратно к средней плоскости. Представим себе, как показано на рис. 41, частицу, откло­нившуюся от средней плоскости СС, и оказавшуюся на расстоянии Z от нее в точке А. На рисунке кривизна силовых линий показана утрированно большой. В действительности в ускорителях силовые линии имеют незначительную кривизну.

Радиус кривизны силовых линий пересекает среднюю линию в точке 0. С достаточной степенью приближения можно считать, что силовые линии представляют собой окружности, проведенные из точки 0 как из центpa. При весьма малой кривизне, которая обычно достаточна для осуществления вертикальной фокусировки в ускорителе описаннoro типа, такое допущение не приводит к существенным ошибкам в дальнейших рассуждениях. Центробежная сила Р_с направлена горизонтально. Лоренцева сила всегда действует в направлении нормали к силовым линиям магнитного поля. Составляющая Р_Н·cosα компенсирует центробежную силу, а на равновесной орбите в точности ей равна Р_с= Р_Н·cosα.

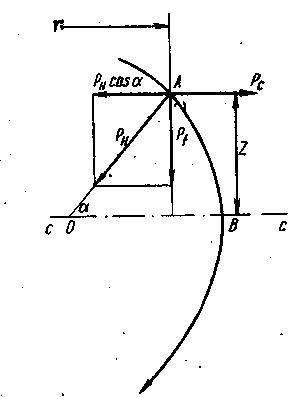
Рис. 41. Векторная диаграм­ма сил, выясняющая при­роду вертикальной фокуси­ровки частиц

Таким образом фокусирующая сила равна

.

Если Z < R, как это бывает в обыч­ных машинах, то Р_Н можно считать по­стоянной и не зависящей от R. В на­ших рассуждениях изменение Z свя­зано с перемещением положения ча­стицы вдоль силовой линии. При Z = 0 частица находится в точке В. Радиус вращения частицы изменится при изме­нении Z. Это вызывает изменение цен­тробежной силы, а следовательно, и равной ей постоянной составляющей P_Hcos a. Обычно отклонение Z порядка 2…3 см, а радиус кривизны силовых линий составляет несколько метров. При этих значениях Z и R величиной Δr можно пренебречь и считать, что фокусирующая сила P_f пропорциональна Z. Нетрудно показать, что при отри­цательном Z, т. е. при отклонении частицы от средней плоскости СС вниз появляется фокусирующая сила, направленная вверх, т. е. сила, стремящаяся, вернуть частицу на среднюю плоскость. Здесь мы имеем дело с вертикальной фокусировкой. Магнитное поле, силовые линии которого имеют конфигурацию, показанную на рис. 40, обладает фокусирующими свойствами. Таким образом, радиальную фокусировку осуществляет механизм, показанный на рис. 38, а вертикальную — механизм, который иллюстрируется рис. 41.

Так как движение частиц в ускорителе происходит без трения, то все частицы, отклоненные от вертикального направления, в средней плоскости совершают незатухающие гармонические к колебания с амплитудой A_z (рис. 42).

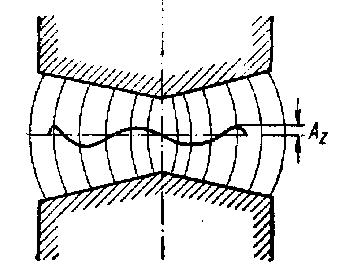
Рис. 42. Свободные верти­кальные колебания частиц

Частота колебаний может быть как меньше частоты обращения частицы, так и больше ее. При движении частиц, устойчивых как в вертикальном, так и в горизонтальном направлении, они могут занимать любое положение внутри некоторой кольцевой области, схематически показанной на рис. 43.

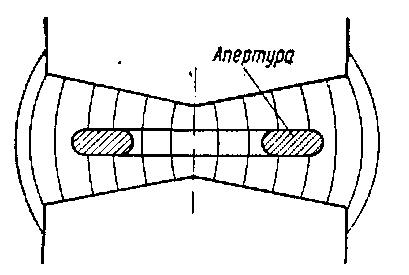
Рис. 43. Область, которую занимают частицы, движущиеся в магнитном поле

вследствие наличия колебаний

Сечение этого кольцевого пространства называется апертурой пучка. Как известно, кривизна силовых линий всегда связана с изменением величины поля в пространстве. В ускорителях необходимая для вертикальной фокусировки кривизна поля обычно создается путем постепенного увеличения зазора между полюсами при увеличении радиуса (см. рис. 7). Напряженность поля в зазоре здесь падает почти обратно пропорционально величине зазора. Изменяя закон, по которому величина зазора зависит от радиуса, можно получить любой закон изменения напряженности поля. Изменение напряженности магнитного поля в зависимости от радиуса орбиты частиц может быть определено формулой

Чем больше n, тем сильнее изменяется магнитное поле в за­висимости от радиуса. На рис. 44 схематически представлены пять вариантов: n = 0; n < 0; n > 1; n = 1; 0 < n < 1.

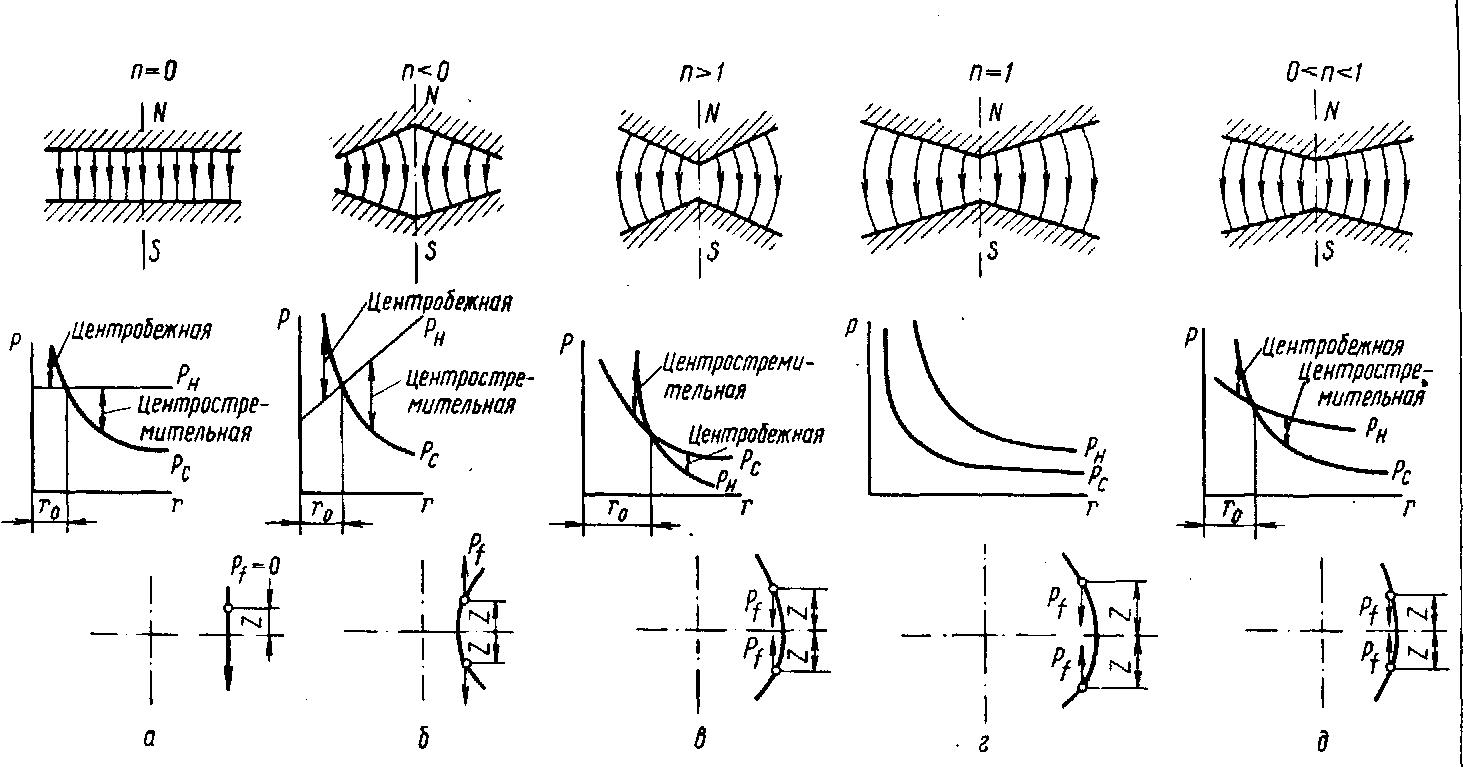
Рис. 44. Схема радиальных и осевых фокусирующих и дефокусирующих сил при различных значениях n

Рассмотрим эти предельные случаи с точки зрения обеспечения устойчивости движения частицы.

Вариант а соответствует п = 0 Н = H₀. Напряженность поля не зависит от радиуса и поле равномерно. Здесь имеется достаточно сильная радиальная фокусировка. Вертикальная фокусирую­щая сила здесь отсутствует, P_f = 0. Частица может свободно перемещаться в вертикальном направлении вдоль силовых ли­ний.

Вариант б соответствует п < 0. Это случай нарастающего по радиусу магнитного поля, что может быть достигнуто постепен­ным уменьшением зазора от центра к периферии сечения магнита. Радиальная фокусировка здесь очень сильная. Однако этот вариант совершенно неприемлем с точки зрения обеспечения вертикальной фокусировки. Как показано на схеме внизу, здесь кривизна силовых линий создает вертикаль­ную деформирующую силу P_f. Это означает, что малейшее от­клонение частицы от средней плоскости приводит к появлению силы, стремящейся еще дальше отклонить ее от первоначального положения. Увеличение дефокусирующей силы растет пропор­ционально отклонению. Устойчивое движение частиц в таком поле, несмотря на наличие сильной радиальной фокусировки, невозможно. Все частицы гораздо быстрее, чем в варианте а, потеряются на полюсах магнита.

Вариант в соответствующий п > 1, характеризуется очень сильным спадом напряженности магнитного поля вдоль радиуса. Такой спад может быть получен при ярко выраженной кониче­ской форме полюсов. Здесь напряженность магнитного поля, а, следовательно, и лоренцева сила обратно пропорциональна радиусу в степени, большей 1. Поэтому кривые центробежной и лоренцевой сил пересекутся в точке, соответствующей равновесной орбиты. Однако, как следует из рис. 44, в движение будет неустойчивым в ра­диальном направлении.

При переходе частиц на радиус, больший, чем r_o, преобладает центробежная сила, а при переходе на радиус, меньший r_o —цен­тростремительна я.

Таким образом, любое отклонение от равновесной орбиты в радиальном направлении приводит к появлению силы, стремящейся увеличить это отклонение. В результате невозможно, обеспечить устойчивость движения частиц и они неминуемо по­теряются на боковых стенках вакуумной камеры.

Вертикальная фокусировка в этой системе оказывается очень сильной. Вследствие большой кривизны магнитного поля малей­шее отклонение от средней плоскости на величину Z приводит к появлению большой вертикальной фокусирующей силы P_f. Вследствие радиальной неустойчивости вариант в непригоден для обеспечения нормального движения частиц.

Вариант г соответствует значению п = 1. Здесь напряженность магнитного поля изменяется обратно пропорционально радиусу так же, как и величина центробежной силы. Поэтому обе кривые — Р_{н и} Р_с представляют собой гиперболы, которые нигде не пе­ресекаются. Частицы в радиальном направлении находятся в безразличном положении. Радиальная фокусировка отсутствует. Вертикальная фокусировка здесь слабее, чем в предыдущем случае, но достаточно сильная. Вариант п = 1 также не может быть применен в циклических ускорителях вследствие неустой­чивости движения частиц.

Вариант д, соответствующий 0 < п <1, обеспе­чивает как вертикальную, так и горизонтальную устойчивость движения частиц. Здесь напряженность магнитного поли, а, сле­довательно, и лоренцева сила падает медленнее, чем центробеж­ная, с увеличением радиуса. Кривые Р_н и Р_с пересекаются в точке r = r_o, соответствующей равновесной орбите. Всякое отклонение частицы от равновесной орбиты в сторону увеличения радиуса приводит к появлению центростремительной, а в сторону уменьшения — центробежной силы. Движение оказывается в ра­диальном направлении устойчивым. Достаточная кривизна си­ловых линий обеспечивает вертикальную фокусировку. Откло­нение частицы от средней плоскости приводит к появлению вертикальной фокусирующей силы P_f. Таким образом, для обес­печения устойчивого движения частиц, как в радиальном, так и в вертикальном направлении необходимо соблюдение усло­вия

0 <n <1.

Это условие называется иногда условием устойчивого движения частиц при мягкой фокусировке. Показатель спада магнитного поля п

Таким образом, показатель спада магнитного поля представляет собой отношение радиуса к напряженности магнитного поля, соответствующей этому радиусу, умноженному на градиент магнитного поля по радиусу.