3.2 Методики уточнённого расчёта нетто-ставок в страховании жизни

Рассмотрим страхование на дожитие с месячными взносами от возраста х на срок n лет. Будем предполагать, что число умерших в течение одного года, то есть в течение года от возраста х до возраста

х + 1 за каждый месяц умирает d_x/12 человек и так далее от возраста х + n – 1 до возраста х + n – d_x+n-1/12 человек. На рисунке 3.1 изображён поток наличности, оживающий финансовые отношения сторон

Рисунок 3.1 – Поток наличности при страховании на дожитие с месячными взносами

Символом обозначается месячная нетто-ставка страхования на дожитие с месячными взносами при уточнённом расчёте по сравнению с упрощённым расчётом, изложенном в пункте 2.6. Для расчёта используем принцип эквивалентности финансовых обязательств сторон, согласно которому современная стоимость А (0) потока наличности, изображённого на рисунке 3.1, равна нулю. Трудность состоит в том, что в схеме сложных процентов дисконтировать денежные суммы можно только на промежутках времени, равных целому числу единиц времени. Поэтому предложим следующую методику расчёта.

Рассмотрим постоянную силу процента , эквивалентную норме доходности i. Эти показатели связаны соотношением [1]

1+ i= (3.3)

а дисконтирующий множитель имеет вид

(3.4)

Предлагается найти искомую нетто-ставку в терминах силы процента и затем в полученной формуле силу процента заменить нормой доходности на основании соотношения (3.3). Современную стоимость всего потока представим в виде

А (0) = А₁ (0) + … + А_n (0) – А_n+1 (0), (3.5)

где А_j (0) – современная стоимость доходов страховой организации, сосредоточенных в j – м году, 1 j n, А_n+1 (0) – современная стоимость расходов страховой организации в n-м году. Тогда

(3.6)

Представим равенство (3.6) в виде

(3.7)

где

(3.8)

(3.9)

Величина В₁, определяемая формулой (3.8), представляет собой сумму геометрической прогрессии, которая определяется по известной формуле

. (3.10)

Величина В₂ из выражения (3.9) является суммой арифметико-геометрической прогрессией и определяется формулой

(3.11)

Нетрудно заметить, что А₂ (0) определяется равенством

или

(3.12)

где величина V определяется равенством (2.3). Аналогично

(3.13)

Подставляя выражения (3.6), (3.12) и (3.13) в равенство (3.5) и проводя преобразования, получим

(3.14)

Из равенства А (0) = 0 и выражения (3.14) находим, что

(3.15)

Так же, как и в разделе 2 выражение (3.15) можно выразить через коммутационные числа в форме

. (3.16)

Исключая из выражения (3.10) и (3.11) силу процента по формуле (3.3), окончательно получим

. (3.17)

Формула (3.16) вместе с (3.17) уточняет известную приближённую формулу (2.25). Проведём на конкретном примере оценку погрешности.

Найдём ежемесячную нетто-ставку при страховании на дожитие от возраста х = 30 лет на срок n = 15 лет при норме доходности i = 0,03. На основании формулы (2.25) получим, что

Оценим теперь величину по формуле (3.16). Для этого вычислим вначале величины В₁ и В₂ по формуле (3.17) :

,

Тогда

Оценим относительную погрешность приближённой формулы:

Таким образом приближённая формула на 1,77 % больше уточнённой. Вывод о превышении приближённой формулы под уточнённой следует и из экономических соображений. Он верен для любого возраста х, любой длительности договора n и процентной ставки i. Действительно, процесс капитализации нетто-фонда понижает тариф. Чем больше норма доходности, тем меньше тариф. В рамках сделанного в пункте 2.6 упрощающего предположения месячные взносы, внесённые за год, в течение года не подвержены процессу капитализации. Их капитализация начинается с даты окончания соответствующего года. Следовательно, накопленный к дате окончания договора нетто-фонд уменьшается, а нетто-ставка увеличивается по сравнению с ситуацией, когда месячный взнос испытывает процесс капитализации начиная с даты его наступления.

Проведём численный анализ относительной погрешности в зависимости от роста нормы доходности i. Экономические соображения указывают на то, что относительная погрешность должна расти, так как с ростом ставки i растёт темп капитализации.

Пусть i = 0,05. Тогда

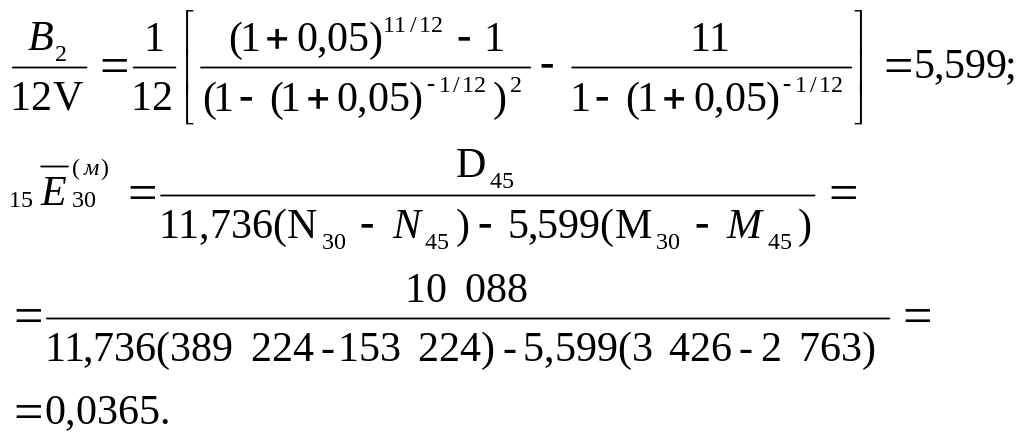
Относительная погрешность . Как и предлагалось, относительная погрешность увеличилась. При этом темп роста составил 234 %.

При норме доходности i = 0,07 аналогично можно получить уточнённую нетто-ставку относительную погрешность и темп роста погрешности 154 % относительно ставки i = 0,05.

Проведём анализ абсолютных погрешностей и соответственно денежных сумм, которые переплачивает страхователь в случае использования приближенных нетто-ставок. Для процентной ставки

i = 3 % абсолютная погрешность рублей в месяц с 1 рубля страховой суммы. Со 100 000 рубля страховой суммы погрешность составит 7,6 рубля в месяц. За весь срок страхования страхователь переплатит 7,6 рубля × 12 месяцев × 15 лет = 1 368 рублей.

Для нормы доходности i = 5 % абсолютная погрешность составит рубля в месяц с 1 рубля страховой суммы. Со 100 000 рублей страховой суммы переплата составит 10 рублей, за весь срок страхования – 1 800 рублей.

Аналогично для нормы доходности i = 7 % переплата со 100 000 рублей страховой суммы составит за весь срок страхования 2 340 рублей.

Следует отметить, что для страхователей увеличение ежемесячных взносов практически несущественно, так как составляет незначительные суммы 7,6 рубля, 10 рублей или 13 рублей. Однако страховая компания по всему страховому портфелю приобретает дополнительно относительно большие денежные суммы. Так, например, при i = 7 % для страхового портфеля объёмом в 1 000 страхователей дополнительно поступает 2 млн 340 тыс. рублей.

По результатам численного сравнительного анализа точной и приближённой формул можно сделать следующие выводы.

1. Классическая приближённая формула для месячной нетто-ставки больше уточнённой формулы.

2. С ростом нормы доходности относительная погрешность между приближённой и уточнённой формулами также растёт.

3. Темп роста относительной погрешности уменьшается с ростом нормы доходности.

4. Абсолютная погрешность несущественна для страхователя.

5. Абсолютная погрешность для страховщика по всему портфелю является достаточно существенной.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Зависит ли тарифная ставка страхования жизни от начального возраста таблицы смертности?

2. Почему тарифная ставка страхования жизни не зависит от числа лиц начального возраста таблицы смертности?

3. Почему важен вывод о независимости тарифной ставки страхования жизни от начального возраста и числа лиц начального возраста таблицы смертности?