2.6. Месячные нетто-ставки страхования жизни

Многие страховые организации предусматривают ежемесячную уплату взносов. При этом накопление страхового фонда происходит по различным законам в течение года и между годами. Накопление за год исчисляется по простым процентам, а накопление от года к году по сложным (если не использовать принцип непрерывного накопления капитала, практикующийся в промышленно развитых странах Запада). При этом страховщики в своих расчётах предполагают, что годичный взнос полностью формируется лишь к концу страхового года, не явно полагая, что взносы вносятся систематически в конце каждого года. При этом накопление от месячных взносов в течение года идёт в пользу страховщиков, не понижая тарифные ставки страхователей. Нетто-ставки, полученные таким способом, носят название годичных нетто-ставок постнумерандо в отличие от годичных нетто-ставок пренумерандо, вносимых в начале каждого страхового года. Тогда месячная нетто-ставка находится делением годичной нетто-ставки постнумерандо на число 12.

Несмотря на то, что при ежемесячных взносах учитывается их капитализация в течение одного года в пользу страховщиков, такая форма страхования выгодна и для страхователей. Она примерно в 12 раз уменьшает величину регулярных платежей, соответствует регулярным доходам подавляющего числа населения (ежемесячная заработная плата), упрощает безналичный перевод денежных средств и т.д.

Найдём месячную нетто-ставку на дожитие от возраста x лет на срок n лет. Для этого вычислим вначале годичную нетто-ставку постнумерандо . На рисунке 2.5 изображён поток наличности, соответствующий таким платежам.

0

Рисунок 2.5 – Поток наличности при страховании на дожитие с годичными взносами постнумерандо

Текущая стоимость этого потока находится по формуле А (0) = _nE_x^{(г,пост)}× ×l_x+nV + …+_nE_x^{(г, пост)}l_x+nVⁿ – l_x+nVⁿ.

Из равенства А(0) = 0 находим, что

или

.

Тогда ежемесячная нетто-ставка на дожитие находится по формуле

. (2.25)

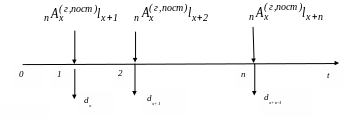
Вычислим ежемесячную нетто-ставку на случай смерти . Поток наличности для годичной нетто-ставки на случай смерти постнумерандо изображён на рисунке 2.6.

. . .

Рисунок 2.6 – Поток наличности при страховании на случай смерти с годичными взносами постнумерандо

Приравнивая текущую стоимость этого потока к нулю, получим уравнение

,

из которого находим, что

. (2.26)

Используя в формуле (2.26) коммутационные числа, получим, что

.

Ежемесячные нетто-ставки на случай смерти находятся по формуле

. (2.27)

Ежемесячная нетто-ставка по смешанному страхованию определяется равенством

. (2.28)

Пример 2.7. Найти ежемесячную брутто-премию по смешанному страхованию для возраста x = 45 лет на срок 10 лет с 10 млн рублей страховой суммы при доле нагрузки 25% и норме доходности i = 0,03.

Решение. Найдём месячную нетто-ставку на дожитие по формуле (2.25):

Аналогично месячная нетто-ставка на случай смерти находится по формуле (2.27)

Нетто-премия по смешанному страхованию согласно формуле (2.28) принимает вид:

Брутто-ставка с 1 рубля страховой суммы:

Т_б = , с 10 млн. рублей страховой суммы Т = 0,01 ×

× 10 000 000 = 100 000 рублей.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Чем основное различие при расчетах нетто-ставок страхования жизни с годичной и единовременной формами уплаты взносов?

2. В чём преимущества ежемесячной формы уплаты взносов по сравнению с годичной и единовременной формами уплаты взносов для страховщиков и страхователей?

3. Какой вид имеет нетто-ставка по смешанному страхованию при ежемесячной форме взносов?