Упражнения
Найти площади фигур, ограниченных линиями:
1).
7).
2).
8).
3).
9).
4).
10).
5).
11).
6).
12).
13). Осью ОХ и
одной аркой циклоиды
14). Астроидой
15).
16).
17).
.
Формулы длин плоских кривых
,
(2.5)
где
-- длина дуги кривой, заданной уравнением
(функция
непрерывна на
вместе со своей производной).
(2.6)
где
-- длина дуги кривой, заданной
параметрическими уравнениями
(функции
и
имеют непрерывные производные на
,
).
(2.7)
где
-- длина дуги кривой, заданной в полярных
координатах уравнением
(функция
имеет непрерывную производную на
).
Пример 2.12. Найти длину полукубической
параболы
,
отсеченной прямой
.
Данная кривая симметрична относительно
оси ОХ. Мы вычислим длину дуги одной
ветви кривой например, верхней) и
результат удвоим. Из уравнения кривой
.
Следовательно, по формуле (2.5) получим:
.
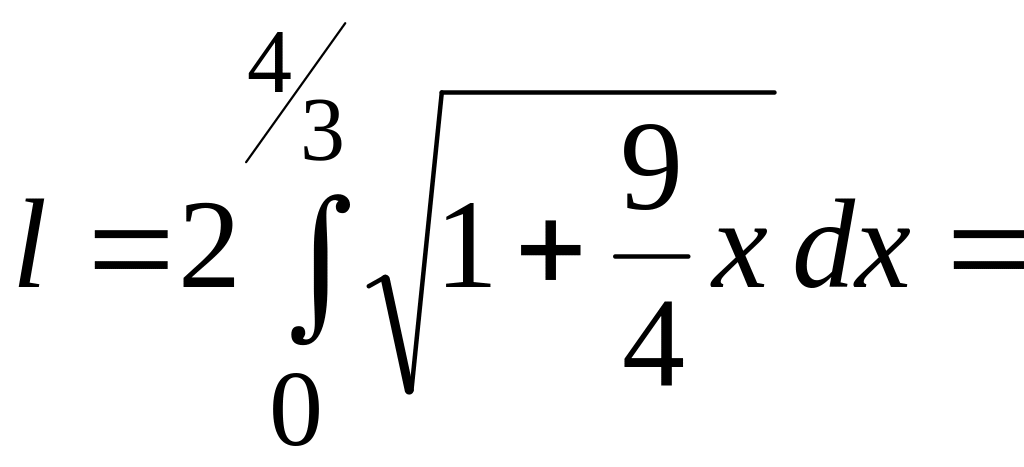
Пример 2.13. Найти длину дуги одной
арки циклоиды
.
Циклоида --- плоская кривая, которую
описывает точка М окружности радиуса
,
катящейся без скольжения по оси ОХ из
начала координат. Из уравнения циклоиды
находим
.
Когда
пробегает отрезок
,
параметр
пробегает отрезок
.
Следовательно, по формуле (2.6) имеем:
.
Пример 2.14. Найти длину дуги кардиоиды (см. рис. в примере 2.11).
Так как кривая симметрична относительно
полярной оси, то для
полярный радиус
описывает половину кривой. Тогда, если
учесть, что
,
формула (2.7) дает:
.
Упражнения
Найти длину дуги кривой.
1).
2).
3).
4).
5).
6).
7).
8). Астроиды
9).
10). Кардиоиды
.
Формулы объемов тел вращения
(2.8)
где
--
объем тела, полученного вращением
криволинейной трапеции
вокруг оси ОХ.
(2.9)
где
--
объем тела, полученного вращением
криволинейной трапеции
вокруг оси ОУ.
Пример 2.14. Найти объем тела,
образованного вращением вокруг оси ОХ
криволинейной трапеции, ограниченной
линиями
.
Изобразим тело вращения. По формуле
(2.8)
.
Пример 2.15. Найти объем тела,
образованного вращением эллипса
вокруг оси ОУ.
Так как эллипс симметричен относительно осей координат, то достаточно найти половину искомого объема и результат удвоить. По формуле (2.9) имеем
