Некоторые геометрические приложения определенного интеграла

Формулы площадей некоторых плоских фигур

, (2.1)

где -- площадь криволинейной трапеции, ограниченной графиком функции , отрезком на оси ОХ и прямыми .

, (2.2)

где -- площадь фигуры, заключенной между графиками функций и , , прямыми .

, (2.3)

где -- площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями непрерывны на , функция монотонна на .

, (2.4)

где -- площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением -- непрерывна на ), и двумя полярными радиусами, составляющими с полярной осью углы и .

Пример 2.7. Найти площадь фигуры, ограниченной параболой , прямой и осью ОХ.

Прежде всего следует начертить эскиз данной плоской фигуры.

Часть фигуры находится над осью ОХ, а

часть—под осью ОХ. Следовательно, учитывая формулу (2.1), находим искомую площадь:

.

Пример 2.8. Найти площадь фигуры, ограниченной прямой и параболой .

В данном случае заштрихованная фигура

ограничена двумя линиями. Следователь

но, для вычисления площади этой фигуры

надо применить формулу (2.2). Для этого

найдем точки пересечения параболы и

прямой. Решая систему ,

получим . Тогда, согласно формуле (2.2), имеем:

.

Пример 2.9. Вычислить площадь эллипса .

Ввиду симметрии кривой относительно осей координат достаточно вычислить площадь части эллипса, находящегося в первой четверти. Поэтому находим

.

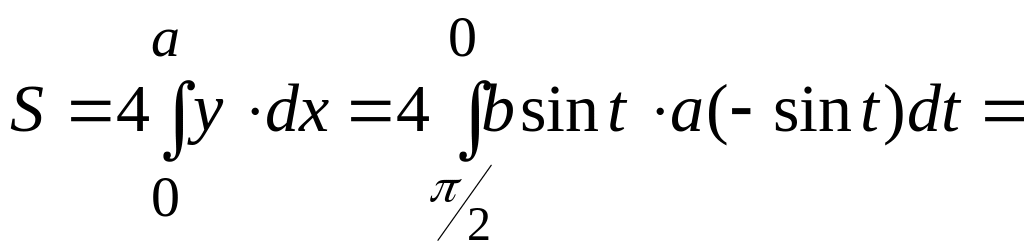
Пример 2.10. Вычислить площадь фигуры ограниченной лемнискатой

.

Предварительно остановимся на описании формы кривой. При полярный радиус кривой , следовательно, кривая проходит через полюс. Из уравнения кривой видно, что принимает действительные значения, когда , то есть когда угол удовлетворяет неравенствам . Откуда , . Заметим, что когда , то полярный радиус описывает часть кривой, расположенной в первой и четвертой четвертях, а при

описывает часть кривой, расположенной во второй и третьей четвертях. Если к тому же учесть, что период равен , то при замене на полярный радиус не изменяется. Таким образом, эта кривая расположена в двух вертикальных углах между прямыми, проведенными под углами и к полярной оси, и пересекает себя сама в полюсе О. Этих соображений уже достаточно для того, чтобы построить всю кривую.

Учитывая симметрию кривой относительно полюса и полярной оси, мы можем ограничиться вычислением площади фигуры, находящейся в первой четверти

. Следовательно, вся площадь фигуры, согласно формуле (2.4) будет равна:

.

Пример 2.11. Найти площадь фигуры, ограниченной кардиоидой .

Так как кривая симметрична относительно полярной оси, в силу четности , то достаточно вычислить площадь верхней половины . Тогда по формуле (2.4) находим:

.