
- •Неопределенный интеграл.
- •Понятие первообразной функции и неопределенного интеграла.
- •Основные свойства неопределенного интеграла.
- •Основные методы интегрирования.
- •1). Непосредственное интегрирование.
- •Упражнения
- •2) Метод подстановки (метод замены переменной).
- •Упражнения.
- •Метод интегрирования по частям.
- •Упражнения.
- •Интегрирование рациональных функций.
- •Упражнения.
- •1.5. Нахождение интегралов вида .
- •Упражнения.
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Основные методы вычисления определенных интегралов
- •Упражнения
- •Некоторые геометрические приложения определенного интеграла
- •Упражнения
- •Упражнения
- •Упражнения
- •3 Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования (несобственные интегралы первого рода)
- •Метод замены переменной в несобственном интеграле
- •Интегрирование по частям в несобственных интегралах
- •Упражнения
- •Упражнения
- •Упражнения
- •Двойной интеграл Определение двойного интеграла и его геометрический смысл
- •Основные свойства двойного интеграла
- •Вопросы для самопроверки
- •Вычисление двойного интеграла
- •Случай криволинейной области.
- •Упражнения
- •Вычислить двойные интегралы (указаны линии, ограничивающие область интегрирования).
- •Двойной интеграл в полярных координатах
- •Упражнения
Основные свойства определенного интеграла
1. Определенный интеграл с одинаковыми
нижним и верхним пределами интегрирования
равен нулю, то есть
![]() .
.
При перестановке пределов интегрирования определенный интеграл меняет свой знак на противоположный.
3. (Свойство аддитивности). Каковы бы
ни были числа
![]() всегда имеет место равенство
всегда имеет место равенство
![]() .
(Предполагается, что функция
непрерывна на большем из трех отрезков
.
(Предполагается, что функция
непрерывна на большем из трех отрезков
![]() ).
).
4. (Свойство линейности). Постоянный
множитель можно выносить за знак
определенного интеграла:
![]() --константа.
--константа.
Интеграл от
суммы (или разности) функций равен сумме
(соответственно, разности) интегралов
от этих функций:
![]() .
.
5. (Свойство
монотонности). Если
![]() и
и
![]() ,
то
,
то
![]() .
.
Формула Ньютона-Лейбница
Если функция
непрерывна на отрезке
и функция
![]() является некоторой ее первообразной
на этом отрезке, то имеет место формула
Ньютона-Лейбница
является некоторой ее первообразной
на этом отрезке, то имеет место формула
Ньютона-Лейбница
![]() .
Введем обозначение для разности
.
Введем обозначение для разности
![]() .
.
Тогда
![]() .
.
Пример 2.1. Вычислить
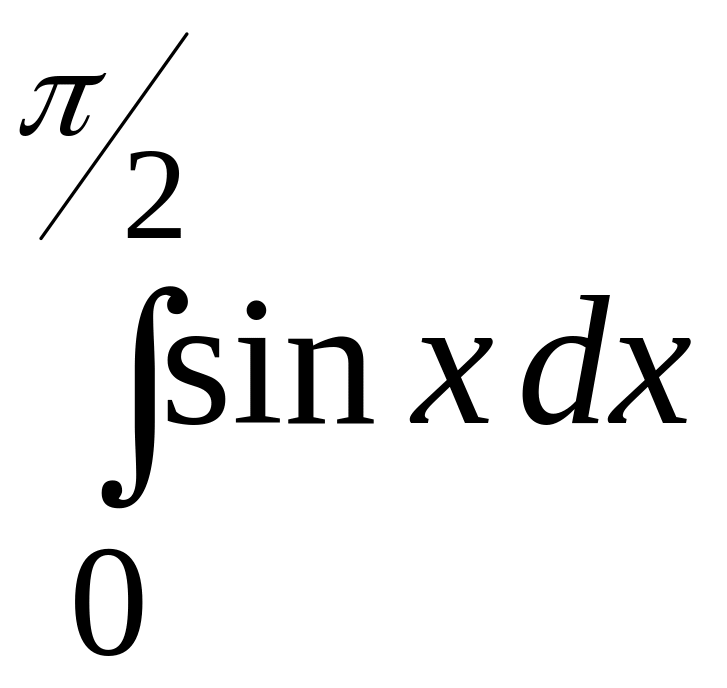 .
.
Так как одна
из первообразных для функции
![]() является функция
является функция
![]() ,
то применяя формулу Ньютона-Лейбница,
получаем
,
то применяя формулу Ньютона-Лейбница,
получаем
 .
.
Основные методы вычисления определенных интегралов
Из пункта 2.3 следует, что вычисление определенных интегралов осуществляется с помощью таблицы неопределенных интегралов. Если же интеграл не содержится в таблице, то следует провести такое преобразование, чтобы получить табличный интеграл.
Этой цели служат основные методы интегрирования, которые подобны применяемым для нахождения неопределенных интегралов, а именно: методы непосредственного интегрирования, подстановки (замены переменной) и интегрирования по частям.
Метод непосредственного интегрирования заключается в том, что данный интеграл представляется в виде суммы или разности табличных.
Пример 2.2. Вычислить
![]()
![]() .
.
Интегрирование подстановкой (заменой
переменной) осуществляется с помощью
следующей формулы (заменой
![]() ):
):
![]() ,
в которой предполагается, что функции
,
в которой предполагается, что функции
![]() и
и
![]() непрерывны на
непрерывны на
![]() и
и
![]() .
.
Если сравнить ее с аналогичной формулой замены переменной в неопределенном интеграле, то основное отличие состоит в том, что в случае вычисления определенного интеграла не обязательно возвращаться к старой переменной. Достаточно вычислить новые пределы интегрирования.
Пример 2.3. Вычислить
![]() .
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Найдем теперь новые пределы интегрирования.
Для этого в замену
подставим пределы интегрирования
исходного интеграла
.
Найдем теперь новые пределы интегрирования.
Для этого в замену
подставим пределы интегрирования
исходного интеграла
![]() и
и
![]() :
:
![]() .
.
В краткой записи решение этого примера выглядит так:
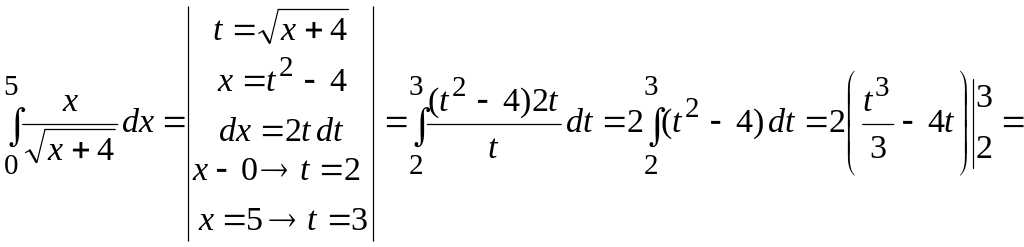
![]() .
.
Пример 2.4. Вычислить
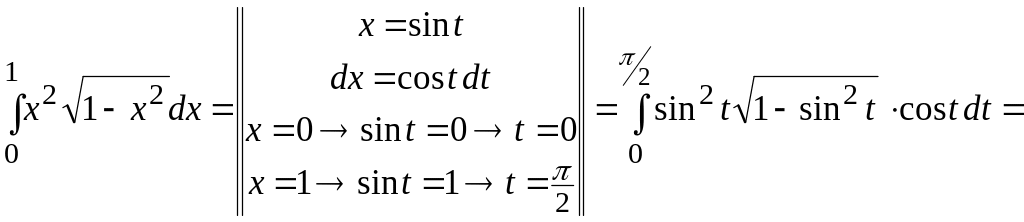
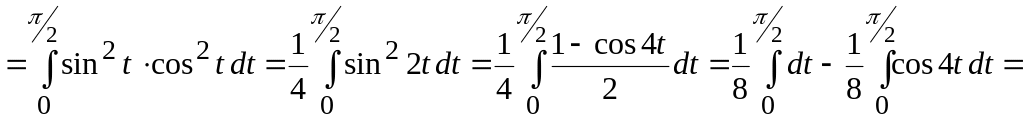
![]() .
.
Интегрирование по частям в определенном
интеграле производится по формуле
![]() ,
в которой предполагается непрерывность
функций
,
в которой предполагается непрерывность
функций
![]() на
.
При этом сохраняются все рекомендации
о том, что взять за
на
.
При этом сохраняются все рекомендации
о том, что взять за
«![]() »,
а что -- за «
»,
а что -- за «![]() ».
».
Пример 2.5. Вычислить
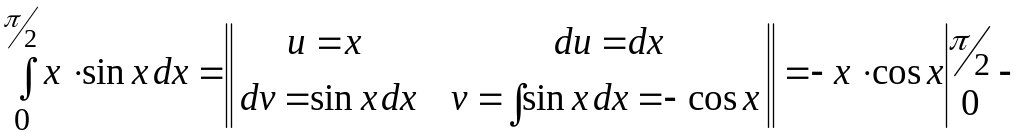
 .
.
Пример 2.6. Вычислить

Упражнения
Вычислить интегралы (в скобках указаны ответы):
1).
![]()
![]() ;
10).
;
10).
![]() ;
;
2).
 ;
11).
;
11).
 ;
;
3).
![]() ;
12).
;
12).
![]() ;
;
4).
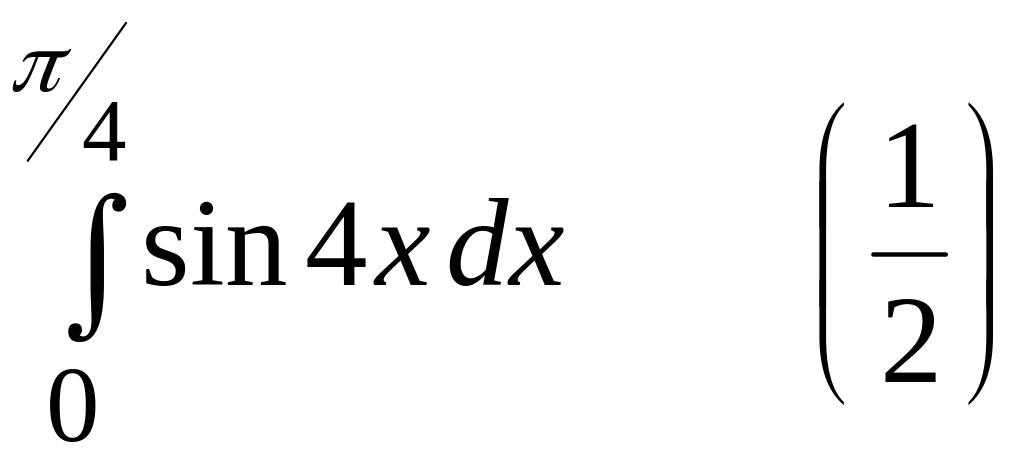 ;
13).
;
13).
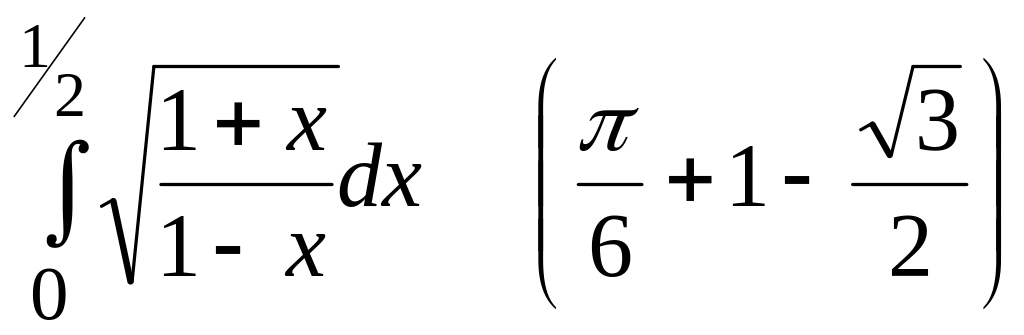
5).
![]() ;
14).
;
14).
![]()
6).
![]() ;
15).
;
15).
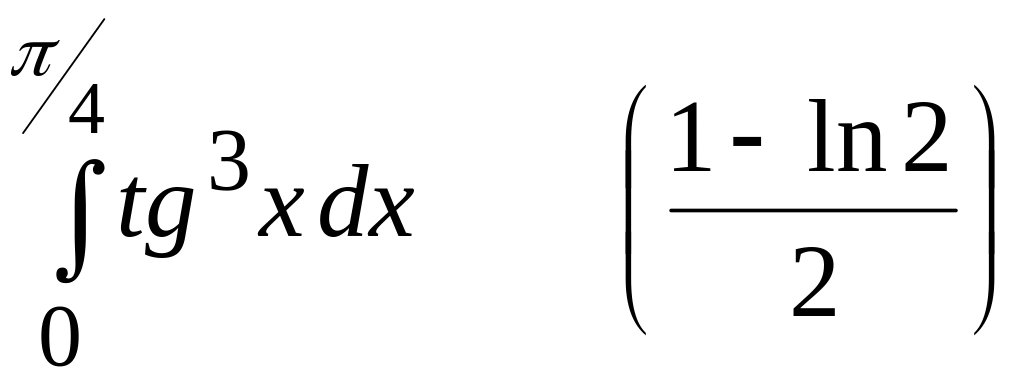 ;
;
7).
![]() ;
16).
;
16).
![]() ;
;
8).
![]() ;
17).
;
17).
![]() ;
;
9).
![]() ;
18).
;
18).
![]() .
.
