
- •Неопределенный интеграл.
- •Понятие первообразной функции и неопределенного интеграла.
- •Основные свойства неопределенного интеграла.
- •Основные методы интегрирования.
- •1). Непосредственное интегрирование.
- •Упражнения
- •2) Метод подстановки (метод замены переменной).
- •Упражнения.
- •Метод интегрирования по частям.
- •Упражнения.
- •Интегрирование рациональных функций.
- •Упражнения.
- •1.5. Нахождение интегралов вида .
- •Упражнения.
- •Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Основные методы вычисления определенных интегралов
- •Упражнения
- •Некоторые геометрические приложения определенного интеграла
- •Упражнения
- •Упражнения
- •Упражнения
- •3 Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования (несобственные интегралы первого рода)
- •Метод замены переменной в несобственном интеграле
- •Интегрирование по частям в несобственных интегралах
- •Упражнения
- •Упражнения
- •Упражнения
- •Двойной интеграл Определение двойного интеграла и его геометрический смысл
- •Основные свойства двойного интеграла
- •Вопросы для самопроверки
- •Вычисление двойного интеграла
- •Случай криволинейной области.
- •Упражнения
- •Вычислить двойные интегралы (указаны линии, ограничивающие область интегрирования).
- •Двойной интеграл в полярных координатах
- •Упражнения
Упражнения
Исследовать сходимость следующих несобственных интегралов.
1)![]() ;
9)
;
9)
![]() ;
;
2)![]() ;
10)
;
10)
![]() ;
;
3)![]() ;
11)
;
11)
![]() ;
;
4)![]() ;
12)
;
12)
![]() ;
;
5)
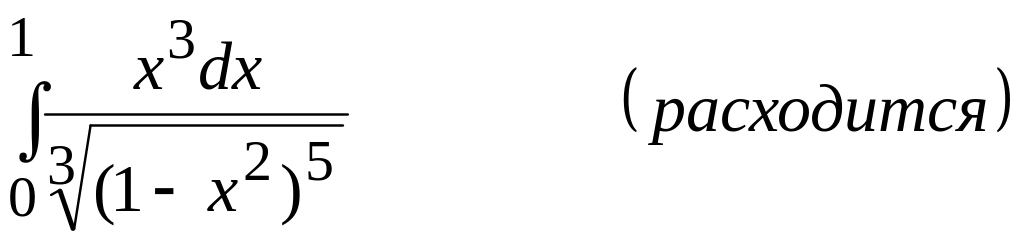 ;
13)
;
13)
![]() ;
;
6)
![]() ;
14)
;
14)
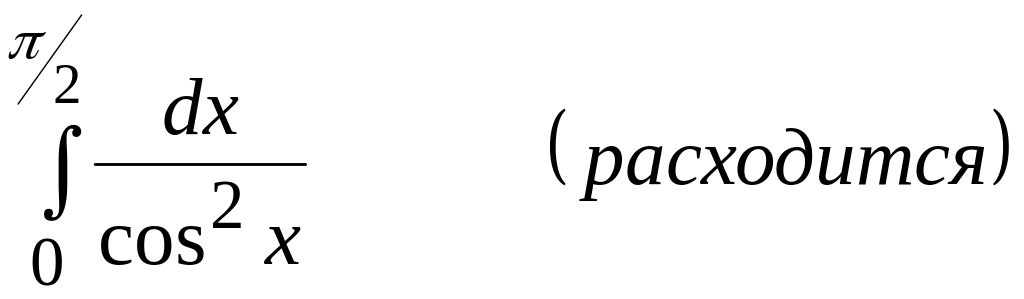 ;
;
7)
![]() ;
15)
;
15)
![]() ;
;
8)
![]() ;
16)
;
16)
![]() .
.
Несобственные интегралы от функций, меняющих знак
Определение 3.3. Пусть функция
непрерывна на
(
--
конечная особая точка или
).
Если наряду с несобственным интегралом
сходится и
![]() ,
то интеграл
называют абсолютно сходящимся, а функцию
называют абсолютно интегрируемой на
.
,
то интеграл
называют абсолютно сходящимся, а функцию
называют абсолютно интегрируемой на
.
Теорема 3.5. (признак абсолютной
сходимости). Если сходится несобственный
интеграл
![]() ,
то сходится
,
то сходится
![]() .
.
Отметим, что из сходимости последнего интеграла, вообще говоря, не следует сходимость . В этом случае говорят, что несобственный интеграл сходится не абсолютно (условно). Соответствующим образом определяются абсолютно условно сходящиеся несобственные интегралы от функций с двумя особыми точками.
Очевидно, если функция
абсолютно интегрируема на
,
а функция
ограничена, то их произведение
![]() будет функцией, абсолютно интегрируемой
на
.
будет функцией, абсолютно интегрируемой
на
.
Сформулируем признак, который позволяет устанавливать сходимость несобственных интегралов в ряде случаев, когда абсолютная сходимость отсутствует.
Признак Дирихле. Пусть функция
непрерывна на
и
![]() монотонная функция на
и
монотонная функция на
и
![]() .
Тогда несобственный интеграл
.
Тогда несобственный интеграл
![]() сходится.
сходится.
Пример 3.13. Исследовать на сходимость
![]() .
.
Здесь функция
![]() абсолютно интегрируема на
абсолютно интегрируема на
![]() ,
так как
,
так как
![]() .
.
В то время как
![]() ,
очевидно, ограничена. Отсюда следует
абсолютная сходимость исходного
интеграла.
,
очевидно, ограничена. Отсюда следует
абсолютная сходимость исходного
интеграла.
Пример 3.14. Исследовать на сходимость
![]() .
.
Пользуясь признаком Дирихле, полагаем
,
а
![]() .
Условия теоремы выполнены, так как
.
Условия теоремы выполнены, так как
![]() и функция
,
монотонно убывая стремится к нулю при
и функция
,
монотонно убывая стремится к нулю при
![]() .
Следовательно, исходный интеграл
сходится.
.
Следовательно, исходный интеграл
сходится.
Можно показать, что этот интеграл при
![]() сходится не абсолютно (см. [1]), а при
сходится не абсолютно (см. [1]), а при
![]() интеграл сходится абсолютно.
интеграл сходится абсолютно.
Пример 3.15. Исследовать на сходимость
![]() .
.
Особая точка у подынтегральной функции
одна:
.
Пусть
![]() ,
тогда
,
тогда
![]() .
.
Следовательно,
монотонно убывает при
![]() .
Кроме того,
.
Кроме того,
![]() .
Далее,
.
Далее,
![]() .
.
В силу признака Дирихле исходный интеграл сходится.
Упражнения
Исследовать следующие несобственные интегралы на сходимость:
1)![]() ;
8)
;
8)![]() ;
;
2)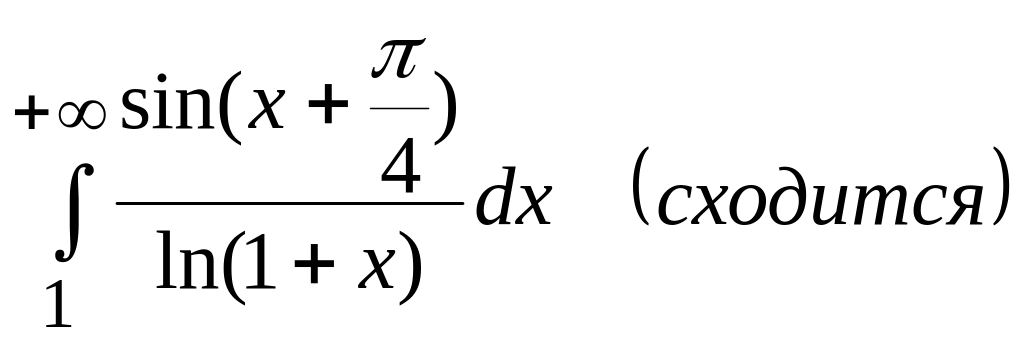 ;
9)
;
9)
![]() ;
;
3)![]() ;
10)
;
10)
![]() ;
;
4) ;
11)
;
11)
![]() ;
;
5)![]() ;
12)
;
12)
![]()
6)![]() ;
13)
;
13)
![]() ;
;
7)![]() ;
14)
;
14)
![]() .
.
Двойной интеграл Определение двойного интеграла и его геометрический смысл
Пусть функция
![]() ,
где
,
где
![]() -- ограниченная замкнутая область в
-- ограниченная замкнутая область в
![]() ,
которая имеет площадь Р (квадрируема).
,
которая имеет площадь Р (квадрируема).
Заметим, что если граница области
состоит из конечного числа непрерывных
кривых, каждая из которых выражается
уравнением вида
![]() и
и
![]() ,
где
и
непрерывные функции, то эта область
квадрируема, то есть имеет площадь Р.
,
где
и
непрерывные функции, то эта область
квадрируема, то есть имеет площадь Р.
Диаметром замкнутой области называется наибольшее расстояние между двумя точками этой области.
Разобьем область
произвольным образом сетью непрерывных
кривых на конечное число частей
![]() ,
,
![]() ,…,
,…,![]() ,
площади которых соответственно обозначим
,
площади которых соответственно обозначим
![]() ,
,
![]() ,…,
,…,![]() .
В каждом из
.
В каждом из
![]() ,
возьмем произвольную точку
,
возьмем произвольную точку
![]() и составим интегральную сумму для
функции
и составим интегральную сумму для
функции
![]() в области
в области
![]() .
.
Обозначим через
наибольший из диаметров частичных
областей
![]() .
.
Определение 4.1. Если интегральная
сумма
![]() при
имеет конечный предел
при
имеет конечный предел
![]() ,
не зависящий ни от способа разбиения
области
на части, ни от выбора точек
,
то этот предел называется двойным
интегралом функции
по области
и обозначается
,
не зависящий ни от способа разбиения
области
на части, ни от выбора точек
,
то этот предел называется двойным
интегралом функции
по области
и обозначается
![]() .
Функция
в этом случае называется интегрируемой
в
.
.
Функция
в этом случае называется интегрируемой
в
.
Замечание. Если
![]() в области
,
то
в области
,
то
![]() .
.
Итак,
![]() (4.1).
(4.1).
Для интегрируемости функции в области достаточно ее непрерывности в . В дальнейшем будем предполагать, что рассматриваемые функции непрерывны в области .
Рассмотрим тело
![]() ,
ограниченное сверху поверхностью
,
ограниченное сверху поверхностью
![]() ,
где
--
неотрицательная и непрерывная в области
функция; с боков – цилиндрической
поверхностью с образующей параллельной
оси OZ, снизу – фигурой
,
лежащей в плоскости XOY.
Тело указанного вида принято называть
цилиндрическим бруском.
,
где
--
неотрицательная и непрерывная в области
функция; с боков – цилиндрической
поверхностью с образующей параллельной
оси OZ, снизу – фигурой
,
лежащей в плоскости XOY.
Тело указанного вида принято называть
цилиндрическим бруском.
Объем данного тела
![]() .
(4.2).
.
(4.2).
Если
![]() в области
,
то
в области
,
то
![]() .
.
