7. Найдем интервалы выпуклости и вогнутости функции и проверим, имеет ли график функции точки перегиба.

Кривая называется вогнутой на интервале , если она лежит выше любой ее касательной на этом интервале.

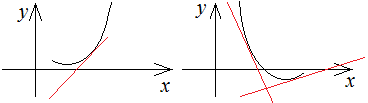
Кривая называется выпуклой на интервале , если она лежит ниже любой ее касательной на этом интервале.

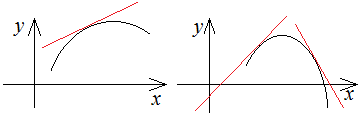
Если функция вогнутая, то , если выпуклая, то .

Поясним связь между знаком второй производной и выпуклостью (вогнутостью) функции геометрически.

Первая производная функции показывает, возрастает или убывает функция. Вторая производная показывает, возрастает или убывает первая производная.

Если первая производная возрастает, то вторая производная положительна (точнее ).

Если первая производная убывает, то вторая производная отрицательна (точнее ).

Первая производная функции, вычисленная в заданной точке, равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной к графику функции в этой точке.

Возьмем несколько точек: , ; ; ; , проведем касательные в этих точках и вычислим соответствующие им угловые коэффициенты.

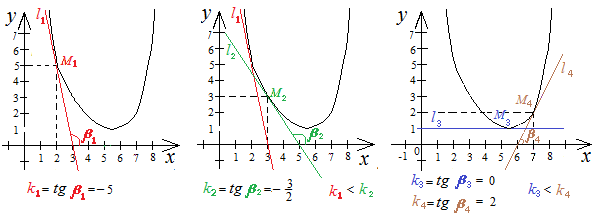
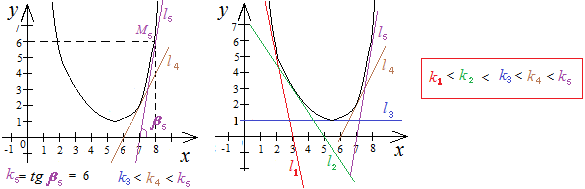
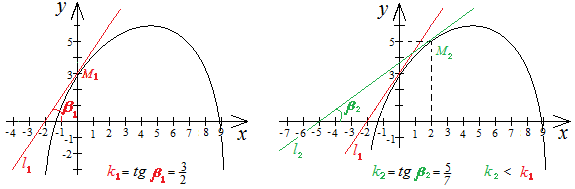
Если функция на интервале вогнутая, то с увеличением значений

угловые коэффициенты соответствующих касательных (и соответствующие значения первой производной) увеличивается. Это значит, что вторая производная должна быть положительна. ( Для любого выполняется , ).

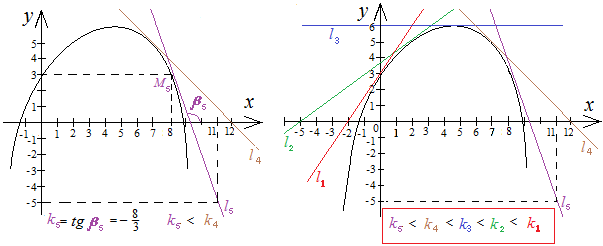
Если функция на интервале выпуклая, то с увеличением значений угловые коэффициенты соответствующих касательных (и соответствующие значения первой производной) уменьшается. Значит, вторая производная должна быть отрицательна (для любого

выполняется , ).

Точка, отделяющая выпуклую часть кривой от вогнутой части, называется точкой перегиба.

Если абсцисса точки перегиба графика функции и в этой точке существует , то .

Следовательно, точками перегиба могут служить только критические точки второго рода, т.е. точки, в которых вторая производная обращается в нуль или не существует. У дробно рациональной функции критическими являются только точки, в которых .

Найдем вторую производную функции и приравняем ее к нулю. Найдем корни полученного уравнения (критические точки). Предположим, что это точки , . Для исследования на выпуклость (вогнутость) на числовую прямую нанесем точки разрыва ( ) и найденные критические точки второго рода ( , ). Точки разрыва исключены из ОДЗ, поэтому мы отметим их как выколотые точки.

Критические точки второго рода и точки разрыва делят ОДЗ на интервалы знакопостоянства второй производной функции. Определив знак второй производной на полученных интервалах, можно сделать выводы об интервалах выпуклости и вогнутости, точках перегиба.

Если на выбранном интервале вторая производная положительна ( ), то график функции на данном интервале вогнутый, если отрицательна ( ), то график функции выпуклый.

Если вторая при переходе через точку критическую точку меняет знак, то эта точка является абсциссой точкой перегиба. Если вторая производная при переходе через критическую точку знак не меняет, то данная точка точкой перегиба не является. Точка исключена из ОДЗ, следовательно, она не является точкой перегиба.

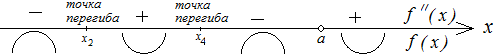
Вычислим значение функции в точках перегиба: и .