
- •План исследования
- •Найдем точку пересечения с осью , нули функции и интервалы ее знакопостоянства.
- •Симметрия графика функции (четность, нечетность функции).
- •И сследуем поведение функции при . Если возможно по одз, найдем пределы: и .
- •Проверим, имеет ли график функции наклонные асимптоты (правые, левые и двусторонние).
- •Найдем интервалы монотонности (возрастания и убывания) функции и точки экстремума.
- •Найдем интервалы выпуклости и вогнутости функции и проверим, имеет ли график функции точки перегиба.
- •Все полученные данные занесем в таблицу.
- •Симметрия графика функции (четность, нечетность).
План исследования
Область допустимых значений; точки разрыва и их характер, вертикальные асимптоты графика.
Точки пересечения графика функции с осями координат.
Симметрия графика функции (четность, нечетность).
Поведение функции при
 и горизонтальные асимптоты графика
функции.
и горизонтальные асимптоты графика
функции.
Наклонные асимптоты графика функции.
Исследование функции с помощью первой производной: интервалы возрастания и убывания, экстремумы функции.
Исследование функции с помощью второй производной: участки выпуклости и вогнутости графика, точки перегиба.
Анализ полученных результатов исследования и построение сводной таблицы.
Эскиз графика.
Отметить на плоскости точки экстремумов, точки перегиба и точки
разрыва. Начертить асимптоты графика. Показать стрелками, куда будет направлен график функции при приближении его к асимптотам и при .
Построение графика функции.
Рассмотрим подробнее все этапы исследования функции и построения ее графика.
Область определения функции (область допустимых значений).
Областью
допустимых значений называется множество
значений переменной
![]() ,
для которых существуют соответствующие
значения
,
для которых существуют соответствующие
значения
![]() .
.
Если
у функции существуют изолированные
точки, в которых функция не определена,
то они будут являться точками разрыва.
Если разрыв существует (например, в
точке
![]() ),
то определим тип разрыва. Для этого
вычислим односторонние пределы: предел
справа
),
то определим тип разрыва. Для этого
вычислим односторонние пределы: предел
справа
![]() и слева
и слева![]() .
.

 Если
при вычислении хотя бы одного из пределов
получим
Если
при вычислении хотя бы одного из пределов
получим
![]() ,
то в данной точке у функции будет разрыв
2 рода и через эту точку проходит
вертикальная асимптота. Ее уравнение
имеет вид
,
то в данной точке у функции будет разрыв
2 рода и через эту точку проходит
вертикальная асимптота. Ее уравнение
имеет вид
![]() .
Эту асимптоту график функции ни когда
не пересекает.
.
Эту асимптоту график функции ни когда
не пересекает.
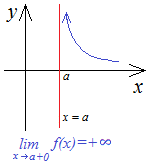
Если
![]() ,
то по мере приближения
,
то по мере приближения
![]() к
справа график функции будет уходить
вверх, приближаясь к вертикальной
асимптоте.
к
справа график функции будет уходить
вверх, приближаясь к вертикальной
асимптоте.
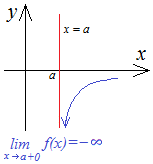
Если
![]() ,
то по мере приближения
к
справа график функции будет уходить
вниз, приближаясь к вертикальной
асимптоте.
,
то по мере приближения
к
справа график функции будет уходить
вниз, приближаясь к вертикальной
асимптоте.

Если
![]() ,
то по мере приближения
к
слева график функции будет уходить
вверх, приближаясь к вертикальной
асимптоте.
,
то по мере приближения
к
слева график функции будет уходить
вверх, приближаясь к вертикальной
асимптоте.

Если
![]() ,
то по мере приближения
к
слева график функции будет уходить
вниз, приближаясь к вертикальной
асимптоте.
,
то по мере приближения
к
слева график функции будет уходить
вниз, приближаясь к вертикальной
асимптоте.
Найдем точку пересечения с осью , нули функции и интервалы ее знакопостоянства.
Чтобы
получить координаты точки 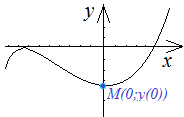 пересечения
с осью
пересечения
с осью
![]() ,
вычислим значение функции при
,
вычислим значение функции при
![]() .
Точка
.
Точка
![]() является точкой пересечения графика
функции с осью
.
является точкой пересечения графика
функции с осью
.
Н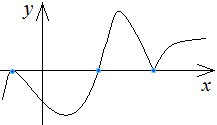 улем
функции
улем
функции
![]() называется такое действительное число
,
при котором значение функции равно 0.
Для того чтобы найти нули функции,
следует решить уравнение
называется такое действительное число
,
при котором значение функции равно 0.
Для того чтобы найти нули функции,
следует решить уравнение
![]() .
Нули функции представляют собой абсциссы
точек, в которых график этой функции
либо пересекает ось абсцисс (ось
.
Нули функции представляют собой абсциссы
точек, в которых график этой функции
либо пересекает ось абсцисс (ось
![]() ),
либо касается ее, либо имеет общую точку
с этой осью. Функция может не иметь ни
одного нуля.
),
либо касается ее, либо имеет общую точку
с этой осью. Функция может не иметь ни
одного нуля.
Чтобы
найти нули функции, положим
![]() и найдем соответствующие значения
аргумента
(или
убедимся в отсутствии корней), если
точные методы решения полученного
уравнения известны. Следует отметить,
что
уравнение
часто
удается решить лишь приближенно.
и найдем соответствующие значения
аргумента
(или
убедимся в отсутствии корней), если
точные методы решения полученного
уравнения известны. Следует отметить,
что
уравнение
часто
удается решить лишь приближенно.
Нули
функции и точки разрыва делят ОДЗ  на
интервалы знакопостоянства функции.
Чтобы определить
знак функции на промежутках между
корнями и точками разрыва, нужно
подставить любое число из рассматриваемого
интервала в исходное уравнение и
определить знак функции.
на
интервалы знакопостоянства функции.
Чтобы определить
знак функции на промежутках между
корнями и точками разрыва, нужно
подставить любое число из рассматриваемого
интервала в исходное уравнение и
определить знак функции.
