36

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧЕРНІВЕЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

імені ЮРІЯ ФЕДЬКОВИЧА

РЕНТГЕНОГРАФІЧНЕ ДОСЛІДЖЕННЯ ТЕПЛОВОГО РОЗШИРЕННЯ

/ Дипломна робота /

Допущено до захисту Зав. кафедрою ФТТ,

” ” червня 2009 р. проф. Раранський М.Д.

Завідуючий кафедрою ФТТ,

доктор фіз.-мат. наук,

професор: Раранський М.Д.

Науковий керівник:

кандидат фіз.-мат. наук,

доцент: Балазюк В.Н.

Виконавець

студентка 5-го курсу,

фізичного факультету: Присунько С.І.

Чернівці - 2009

анотація

В роботі рентгендифрактометричним методом визначено температурні зміщення рентгенівських інтерференцій порядків (303) і (0 0 12) в інтервалі температур 80-300 К.

Розраховано компоненти тензора теплового розширення монокристалів In_1,03Se_0,97.

Робота написана українською мовою, містить 37 сторінок машинописного тексту, 12 рисунків, 3 таблиці, список цитованої літератури і 2 додатки.

ЗМІСТ

ВСТУП 4

Розділ І. АНАЛІТИЧНИЙ ОГЛЯД

1.1. Мікроскопічна теорія термічного розширення 6

1.2. Феноменологічна теорія теплового розширення 10

1.3. Рентгенівський метод дослідження теплового розширення твердих тіл 13

1.4. Тензор термічного розширення 16

1.5. Методика рентгенографування при низьких температурах 17

Розділ II. РЕЗУЛЬТАТИ ДОСЛІДЖЕННЯ ТА ЇХ ОБГОВОРЕННЯ

2.1. Діаграма стану системи In-Se 20

2.2. Рентгеноструктурні дослідження сполуки In_1,03Se_0,97 21

2.3. Термічне розширення сполуки In_1,03Se_0,97 25

ВИСНОВКИ 30

ЛІТЕРАТУРА 31

Додаток 1

ТЕХНІКА БЕЗПЕКИ ПРИ РЕНТГЕНОГРАФІЧНИХ ДОСЛІДЖЕННЯХ 32

Додаток 2 34

ВСТУП

Досягнення фізики твердого тіла безпосередньо впливають на розробку нових матеріалів з покращеними або принципово новими фізичними властивостями. Відомо, що багато властивостей твердих тіл, визначаються не тільки кристалічною структурою і розподілом електронів в ній, але й характером коливань атомів в ґратці. Експериментальне вивчення багатьох фізичних явищ твердих тіл в широких інтервалах температур вимагає врахування специфіки коливного руху атомів в вузлах кристалічної ґратки реальних кристалів, тобто особливостей, пов’язаних з ангармонічними ефектами. Ангармонійність – універсальна властивість твердих тіл і найбільш загальне проявлення її визначається в порушені динамічної залежності коливних мод. Взаємодія між ними приводить до комплексного зсуву частот нормальних коливань. Фізична інтерпретація цілого ряду явищ і експериментальних даних стає неможливою без врахування ангармонійності. Ангармонічним характером коливань атомів пояснюється цілий ряд фізичних ефектів: теплове розширення, відмінність між теплоємністю при постійному об’ємі та постійному тиску між ізотермічними і адіабатичними модулями, а також між їх залежностями від температури і тиску. Ангармонійність впливає на процеси пружного і не пружного розсіювання кристалами рентгенівських променів, електронів, нейтронів, гамма квантів та інших випромінювань.

Отже, врахування ангармонічних ефектів в динаміці кристалічних ґраток важливе як із принципової сторони, так і з практичної точки зору. Це означає, що оскільки всі тіла по своїй природі ангармонічні, то при інтерпретації і аналізі експериментальних даних, врахування впливу ангармонійності теплових коливань атомів в кристалічній ґратці на вище згадані властивості кристалів, стає необхіднім і суттєвим.

Основними напрямками розвитку сучасних досліджень в області динаміки ґратки є розробка і створення теоретичних і експериментальних методів вивчення кристалів із складною кристалічною структурою. Перспективними і прямими методами експериментального вивчення досліджуваних сполук являються рентгендифрактометричні та акустичні. Найповнішу інформацію про вплив ангармонізму теплових коливань атомів в кристалічній ґратці на термічні властивості твердих тіл можна дістати, визначивши температурні залежності всіх незалежних компонент тензора теплового розширення _kl (Т). Знання температурної залежності коефіцієнтів термічного розширення дає можливість оцінити вплив температури на ширину забороненої зони, оскільки температурний вплив залежить від двох ефектів: розширення кристалічної ґратки і електрон-фононної взаємодії.

В якості об’єкту дослідження були вибрані кристали In_1,03Se_0,97. Сполука InSe – перспективний напівпровідниковий матеріал для приладів ІЧ-техніки, який зберігає стабільні фізичні параметри по часу, поверхневі властивості якого, практично нейтральні до абсорбції. Однією із особливостей цієї сполуки є різко виражена анізотропія фізичних властивостей, зумовлена шаруватістю структури і анізотропією хімічного зв’язку.

Метою роботи було дослідити: а) вплив відпалу на структурну досконалість кристалів In_1,03Se_0,97; б) термічне розширення досліджуваних кристалів в діапазоні температур 80-300К.

Отримані в роботі термічні характеристики In_1,03Se_0,97 можуть бути безпосередньо використані при інженерних розрахунках для оцінки величини механічних і термічних напруг, які виникають в досліджуваних кристалах при різних зовнішніх впливах (градієнтах температур, тисків, деформацій), а також при конструюванні напівпровідникових приладів на основі цих матеріалів.

Розділ і. Аналітичний огляд

1.1. Мікроскопічна теорія термічного розширення

Взаємодія атомів твердого тіла складається із сил електростатичного притягання і сил відштовхування. Ці сили змінюються по різному при зміні відстані між взаємодіючими частками.

Зміна об’єму кристалу при зміні температури обумовлена несиметричністю результуючого потенціалу взаємодії в кристалічній гратці. Несиметричність або ангармонізм результуючої сили проявляється в гратці, як взаємодія коливань фононного спектру. Степінь зміни характеризується об’ємним коефіцієнтом теплового розширення.

По визначенню, коефіцієнтом теплового розширення називається відносна зміна об’єму при нагріванні тіла на один градус при постійному тиску і записується у вигляді:

, (1.1.1)

де V - об’єм твердого тіла.

Розглянемо взаємодію двох окремо взятих атомів, які знаходяться в положенні рівноваги: сила притягання рівна силі відштовхування. Нехай один атом закріплений. Якщо вивести другий атом з положення рівноваги, то він почне коливатись відносно деякого середнього положення. Якщо сила, що повертає атом в положення рівноваги, пропорційна зміщенню, тобто виконується закон Гука, то середнє положення атома не буде залежати від амплітуди його коливань. Якщо вважати, що коливання атома виникають внаслідок нагрівання, то можна зробити висновок, що середні розміри такої двохатомної моделі тіла не залежать від температури. Потенціальна енергія двох таких атомів являє собою параболу, яка відповідає гармонічним коливанням (пунктирна лінія, рис.1а).

В дійсності, енергія взаємодії двох атомів повинна бути зображена р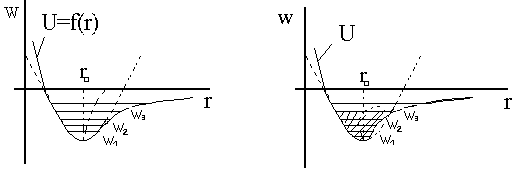 ізко асиметричною кривою (суцільна лінія, рис. 1а), яка являє собою результати накладання двох різних кривих – кривої, що відповідає притяганню і кривої, що відповідає відштовхуванню атомів.

а) б)

Рис. 1. U=f(r) крива потенціальної енергії, штрихована лінія – гармонічне наближення; точки – зміщення положення рівноваги при зміні повної енергії; а) звичайний вигляд кривої U=f(r); б) можливий вигляд кривої U=f(r) в припущенні, що існує від’ємний коефіцієнт теплового розширення.

Найчастіше потенціальна енергія сил взаємодії між атомами описується за допомогою потенціалу Ленарда - Джонса:

, (1.1.2)

тут А і В – константи, r – відстань між взаємодіючими атомами.

В усіх випадках n>m і чим більше енергія взаємодії відхиляється від параболи, тим більша ця нерівність. Таким чином для лівої частини кривої, яка відповідає потенціальній енергії взаємодії двох атомів, основну роль відіграють сили відштовхування, для правої – сили притягання. r₀ –рівноважна віддаль між атомами, що відповідає мінімуму потенціальної енергії. Поки амплітуда коливань атома поблизу положення рівноваги мала, сила, що діє на атом, пропорційна зміщенню F=-ax (гармонічне наближення). З ростом амплітуди коливань сила відштовхування між атомами при їх зближенні росте швидше ніж сила притягання при віддалені одного атома від іншого. Отже, сила, що діє на атом, в цьому випадку не являється лінійною функцією зміщення [1,3,4].

Розглянемо коливання одного атома відносно іншого при заданій повній енергії в класичному наближенні. Нехай різні значення повної енергії зображаються горизонтальними лініями W₁, W₂, W₃ …(рис. 1а) [1]. В положенні рівноваги r=r₀ потенціальна енергія атома рівна нулю, а кінетична максимальна. При віддалені атома від положення рівноваги, потенціальна енергія його росте і досягає свого максимального значення при найбільшому зміщенні атома від положення рівноваги, що відповідає точкам перетину кривої потенціальної енергії з горизонтальною прямою W.

По мірі росту енергії атома W₁, W₂, W₃,… росте амплітуда його коливань. При цьому зміщення атома вправо більше, ніж зміщення вліво. В результаті середнє положення між атомами відхиляється від r₀ вправо і тим більше, чим більша енергія атома, що коливається.

Отже, ріст кривої енергії (або температури) атома приводить до того, що середня відстань між атомами збільшується. Застосовуючи це до кристалу, видно, що із ростом енергії (температури) він обов’язково буде розширюватись.

На основі цієї простої двохатомної моделі твердого тіла, Фермі [1] і Френкелем [2] була виведена елементарна формула для коефіцієнта теплового розширення.

Для малих коливань атомів кристалу, поблизу положення рівноваги, потенціальну енергію атома U(r) можна розкласти в ряд по степеням зміщення атомів відносно положення рівноваги. Ангармонізм у цій двохатомній моделі буде враховуватись членом третього порядку в розкладі для потенціальної енергії:

(1.1.3)

Проведемо заміни: U(r)=U₀ ; r- r₀=х, ; .

Тоді, враховуючи , отримаємо

, (1.1.4)

де .

Коефіцієнт а – це коефіцієнт квазіпружного зв’язку, b – коефіцієнт ангармонійності. Сила, що діє на атом, який коливається зі сторони закріпленого атома, рівна:

, (1.1.5)

тут до пропорційного зміщення додається член, який враховує асиметрію сили взаємодії між атомами. Доданий член в першому наближенні пропорційний коефіцієнту ангармонійності b і має той самий знак. Абсолютна величина поправки тим більша, чим більше зміщення х.

Середнє значення сили, яка діє на атом, що коливається, рівне нулю, тобто , при цьому середнє значення зміщення .

Якщо не враховувати квадратичну поправку (вважати b=0), то середнє значення буде рівне нулю. З точністю до величини другого порядку величину можна замінити її значенням в гармонічному наближенні. Тоді середня потенціальна енергія теплових коливань буде рівна , тобто

, (1.1.6)

k – постійна Больцмана, T – температура.

Коефіцієнт теплового розширення для двохатомної моделі α може бути визначений, як відношення середнього зміщення r₁-r₀ до початкової відстані між атомами r₀, тобто: .

Використовуючи (1.1.6) для , отримаємо

(1.1.7)

Із (1.1.7) видно, що дійсно у випадку відсутності ангармонізму(b=0) коефіцієнт розширення α рівний нулю. Хоч була вибрана елементарна двохатомна модель [3] і зроблено ряд припущень, однак ця формула дає правильний порядок величини коефіцієнта теплового розширення. З (1.1.7) також слідує, що коефіцієнт теплового розширення α прямо пропорційний коефіцієнту ангармонійності і має однаковий з ним знак. Числове значення коефіцієнта теплового розширення визначається не тільки величиною b, але також і величиною коефіцієнта квазіпружнього зв’язку а.