2.4 Расчет плиты в наклонных сечениях

Рис. 7

Поперечную арматуру принимаем при сварке с рабочей арматурой (Ø6А240С). Шаг хомутов в приопорных зоне Sw1 ≤ h / 2, в середине пролета - Sw2 ≤ 0.75h. Принимаем Sw1 = 150 мм, Sw2 = 250 мм.

В работе на поперечную силу вместе с ребрами участвует и часть

полки шириною

b₁ = b + 3h_f = 16 + 3х5 = 31 см, (Рис. 7)

поэтому несущая способность сечения на поперечную силу увеличивается на

величину

φ_f = 0.75h_f'(b_f' – b) / bh₀ = 0.75×5(31 – 16)/16×31 = 0.113<0,5.

Проверка:

1. Проверяем условие

Q_max≤ 0.3φ_b1φ_w1R_bbh₀₌0,3х1,098х0,885х1,15х16х31=163≥56,25

откуда коэффициент поперечного армирования:

µ_w = A_sw/b_sw1 = 0.57/15*15 = 0.00253;

ν = E_s/E_b = 2100 / 270 = 7.7;

коэффициент влияния поперечного армирования

φ_w1 = 1 + 5νµ_w = 1 + 5х7.7х0.00253 = 1.098;

коэффициент φ_b1 = 1 – 0.01R_b = 1 – 0.01х11.5 = 0.885 ( R_b – в МПа).

2. Определяем несущую способность бетона

Q_b.min = φ_b3 (1+φ_f)R_btbh₀ = 0.6×1.113×0.09×16×31 = 29,8 кН. < Q_max=56,25

Хомуты требуются по расчету

3. Погонная несущая способность поперечной арматуры

q_sw = RswAsw/S_w = 17.5×0.57 / 15 = 0.665 кН/см;

проверка: φ_b3 (1+φ_f)R_btb/2 = 0.6×1.113×0.09×16/2 = 0.48 < 0.665 кН/см.

4. Проекция наклонной трещины

с₀ = 2 х(1+ φ_f )хR_btх bхh₀²/ q_sw = 68.1 см;

проверка: h₀ < c₀ < 2h₀ не выполняется, принимаем с₀ = 2h₀ = 62 см.

j_b2 (1 + j ) R_btbh₀²

f

Q_b = , де φ_b3 = 2,0; с = с₀ = 62 см.

c

2(1+ 0.113) 0.09´16´ 31²

Q_b =

= 49.7 кН.

62

Принимаем Q_b = 49.7 кН.

Потому что Q_b = 49.7 кН < Q_max = 56,25 кН, необходимо рассчитывать хомуты

5. Несущая способность поперечной арматуры

Q_sw = q_swc₀ = 0.665×62 = 41.2 кН.

6. Несущая способность сечения

Q_sect = Q_b + Q_sw = 49,7 + 41.2 = 90.9 кН > Q_max = 56,25 кН.

Окончательно оставляем предварительно принятую поперечную арматуру. (Рис. 8)

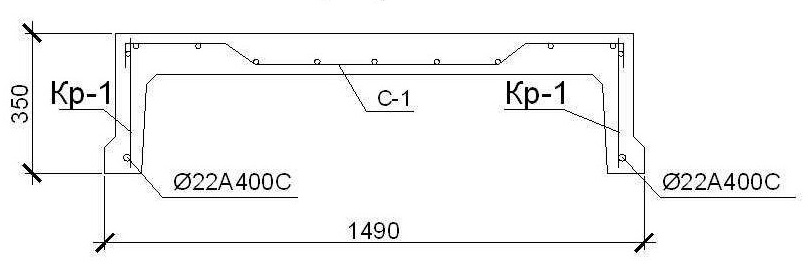
Рис. 8

2.5. Статистический расчет ригеля.

Конструктивная длина ригеля равна (рис. 9).

l_{констр.} = l₀₁ + 150 мм – h_к/2 – зазор = 7950 + 150 – 200 – 50 = 7850 мм.

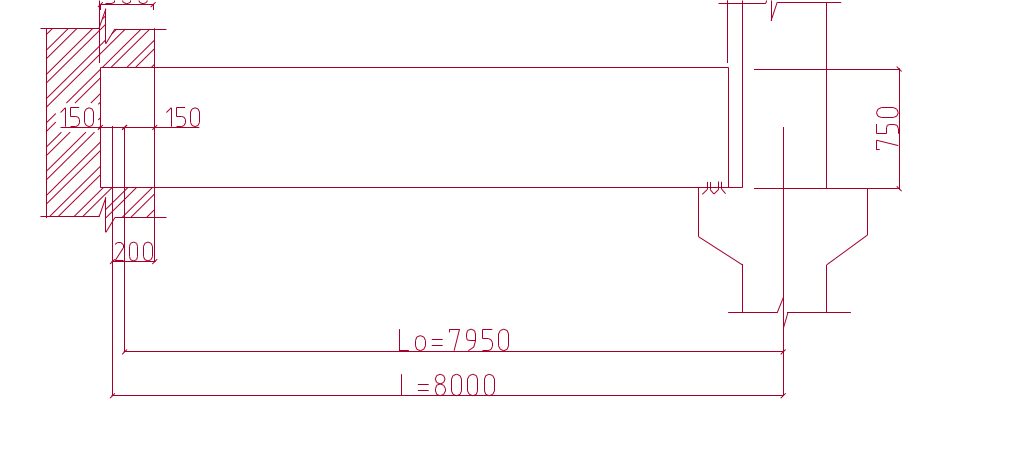
Рис. 9

Расчетное погонная нагрузка

– Постоянная g = g_1м²l + γ_f ×( собственный вес нижней части ригеля) =

= 3.78×5,5 + 1.1(0.4×0.62)25 = 27.61 кН/м;

– Переменная v = v_1м²l = 11,4×5,5 = 62,5 кН/м;

– Полная q = g + v = 27.61 + 62,5 = 90,11 кН/м.

Для расчета крайней пролета рассматривают две расчетные схемы, из которых определяют изгибающие моменты и поперечные силы.

Расчетная схема ригеля многопролетной балки (рис. 10)

Рис. 10

М = (ag + bv)l₀² V = (gg + dv)l₀

М₁ = (0.077×27.61 + 0.1×62,5) 7,95² = 529 кНм;

М_Б = (–0.107×27.61 – 0.121×62,5)7,95² = – 664 кНм;

Q_A = (0.4×27.61 + 0.45×62,5)7,95 = 311 кН;

Q_Б = (–0.6×27.61 – 0.617×62,5)7,95 = – 438 кН.

За счет перераспределения усилий расчетные изгибающие моменты в

пролете и на опоре

М_прол = 0.9 М₁ = 0.9×529 = 476 кНм;

М_Б = /0.75М_В / = 0.75×664= 498 кНм.

Этот момент М_Б попадает пиковым значением в колону, ав ригеле на границу с колоной.

М_опр= М_Б-( |Q_Б.лев|-h_ко)/2=498-(438х0,4)/2=410 кНм