3. Кинетический момент ротора гироскопа

Для уяснения физической сущности кинетического момента воспользуемся понятием "количество движения".

Количеством движения материальной точки называется произведение массы этой точки на её линейную скорость.

Л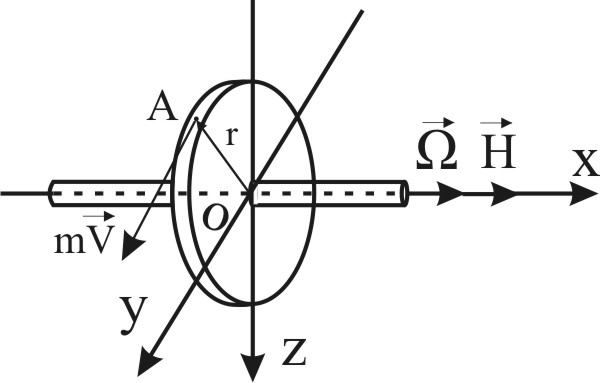 инейная скорость точки - вектор, следовательно, количество движения также вектор, приложенный к движущейся точке и совпадающий по направлению с вектором линейной скорости (рис. 5).

На рис. 5 изображен гироскоп, вращающийся с угловой скоростью Ω. Выделим в теле ротора _j гироскопа материальную точку А с элементарной массой т. Эта точка движется по окружности радиусом r с линейной скоростью V .числовое значение которой V = r ·Ω . Вполне очевидно, что вектор количества движения mV точки А направлен по касательной к окружности, описываемой точкой.

Рис.5 Моментом количества движений материальной точки (h) относительно оси называется произведение количества движения этой точки на её расстояние до оси вращения. Применительно к ротору гироскопа имеем:

; (5)

Вектор момента количества движения строят на оси вращения и направляют в сторону, с которой вращение точки усматривается против движения часовой стрелки.

Взяв множество точек на роторе, просуммировав их моменты количества движения, получим главный момент количества движения ротора гироскопу Н:

(6)

Так как угловые скорости всех точек вращающегося ротора одинаковы, поэтому

(7)

В равенстве (7) надо учитывать, что угловая скорость вращения и главный момент количества движения - векторные величины.

Главный момент количества движения (Н) ротора гироскопа относительно оси вращения называется кинетическим моментом.

4. Теорема об изменении кинетического момента

Эта теорема определяет закон изменения вектора кинетического момента Н при действии на вращающееся тело моментов внешних сил. Этот закон имеет несколько формулировок, одна из которых относится к изменению кинетического момента системы относительно точки, которая и будет нас интересовать, т.к. главная ось гироскопа совершает движение относительно неподвижной точки -точки подвеса гироскопа.

Теорема об изменении вектора кинетического момента, или закон моментов, применительно к гироскопу формулируется следующим образом.

Производная по времени от вектора кинетического момента вращающегося гироскопа относительно точки равна вектору главного момента всех внешних сил ( L ), действующих на гироскоп, относительно той же точки

L =dH/dt (8)

Анализ формулы (8) показывает, что кинетический момент величина переменная и является функцией времени. Во всех случаях изменение вектора Н во времени определяется вектором главного момента внешних сил (L), приложенных к гироскопу. Если векторы Н и L совпадают или диаметрально противоположны, то L характеризует изменение модуля Н. Если Н и L взаимно перпендикулярны, то L характеризует изменение только направления вектора Н. Если Н и L составляют угол, отличный от О⁰ , 90°, 180°и 270° то L характеризует и изменение модуля вектора Н, и изменение его направления.

Известно, что производная по времени от вектора равна линейной скорости движения конца этого вектора, т.е.

dH/dt = V (9)

где: V - вектор линейной скорости конца вектора Н. Сравнивая формулы 8 и 9, можно написать

V=L (10)

Р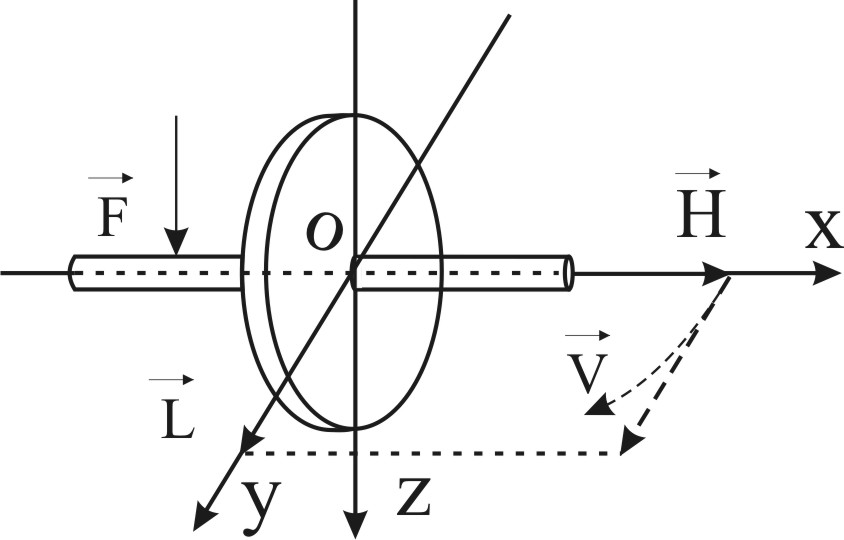 авенство (10) дает геометрическое толкование теоремы об изменении кинетического момента, известное под названием теоремы Резаля.

Теорему Резаля применительно к вращающемуся гироскопу можно сформулировать так: вектор линейной скорости V конца вектора кинетического момента Н гироскопа относительно точки подвеса 0, равен вектору главного момента L всех внешних сил, действующих на гиро-

Рис. 6 скоп, относительно той же точки.

Анализ закона моментов показывает, что под действием момента L внешней силы F вектор Н (главная ось X гироскопа) будет перемещаться в инерциальном пространстве не в направлении действия внешней силы, а в направлении действия момента этой силы, (рис.6).

Этот закон имеет значение для понимания физической сущности свойств гироскопа.