Лекция №2 динамические характеристики гироскопа

К динамическим характеристикам (параметрам) гироскопа относятся:

1. Угловая скорость вращения ротора.

2. Момент инерции ротора.

3. Кинетический момент.

Рассмотрим последовательно каждую из перечисленных динамических характеристик гироскопа.

1. Угловая скорость вращения ротора.

Вращение любого твердого тела характеризуется тремя элементами:

• положением оси, вокруг которой происходит вращение;

• направлением самого вращения;

• величиной угловой скорости вращения.

Этими же элементами характеризуется и вращение гироскопа.

Собственное вращение ротора происходит вокруг его оси симметрии - главной оси гироскопа с определенной угловой скоростью. Угловой скоростью вращающегося ротора (Ω)называется величина, учитывающая скорость изменения угла поворота ротора (У). Аналитическая запись этого определения имеет вид:

Ω =dy/dt (1)

Условно все элементы собственного вращения ротора гироскопа изображаются вектором угловой скорости Ω,. Вектор Ω. направлен по оси, вокруг которой происходит вращение и в ту сторону, откуда вращение наблюдается против движения часовой стрелки (рис.4). Величина вектора изображает в определенном масштабе величину угловой скорости вращения.

Угловая скорость вращения определяется числом радиан в секунду или в технике числом оборотов в минуту.

Соотношение числа оборотов в минуту и числа радиан в секунду определяется выражением:

Ω =π·n/30 (рад/сек) (2)

n = 30·Ω/π (об/мин) (3)

где n - число оборотов в минуту.

Р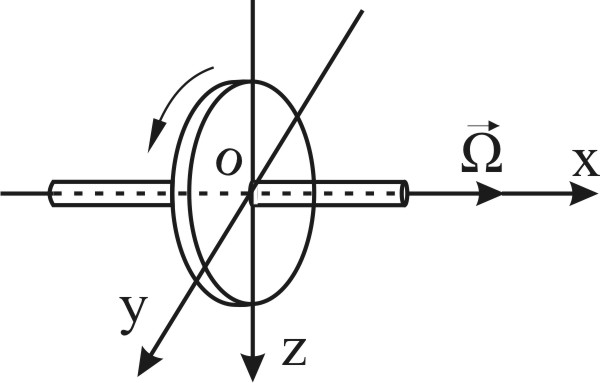 отор гироскопа с тремя степенями свободы имеет возможность вращаться не только вокруг главной оси Х, но и вместе с ней вокруг оси У или Z. Если вращающийся гироскоп поворачивается вокруг оси У или Z, то вектор результирующей угловой скорости можно представить в виде двух составляющих: вектора угловой скорости вращения главной оси гироскопа вокруг оси У или Z и вектора угловой скорости собственного вращения ротора Ω. Угловая скорость вращения ротора

Рис.4 может достигать 10000 - 30000 об/мин, и во много раз больше скорости вращения гироскопа вокруг оси У или Z . Пренебрегая по малости угловой скоростью вращения гироскопа вокруг осей У и Z, результирующую угловую скорость вращения можно считать равной Ω и направленной по главной оси Х гироскопа.

2. Момент инерции ротора

При прямолинейном движении величина массы тела создает определенное препятствие изменению линейной скорости этого движения. Следовательно, масса тела есть мера его инертности.

Если тело совершает вращательное движение, то масса полностью не определяет инертность тела, т.к. кроме численного значения массы тела, необходимо знать ещё и ее размещение относительно оси вращения.

Величина, которая учитывает и массу тела, и её распределение относительно оси вращения, называется моментом инерции (I)

Таким образом, момент инерции является мерой инертности тела, вращающегося вокруг некоторой оси.

Момент инерции ротора гироскопа относительно его, оси вращения (главной оси) равен сумме произведений массы каждой частицы ротора на квадрат расстояний этой частицы от данной оси Х или определенному интегралу, взятому по всему объему ротора (V) гироскопа от произведения бесконечно малой массы m точки ротора на квадрат расстояния (r) от этой точки до оси вращения, т.е.

, или , (4)

где: m_i – масса точки тела; ρdV– масса малого элемента объёма тела; ρ – плотность; r – расстояние от элемента до оси Х.

Момент инерции ротора I величина скалярная. Из выражения (4) следует, что чем дальше от оси вращения расположена основная масса ротора, тем больше его момент инерции.

Для увеличения момента инерции ротору придают форму утолщенного по краям диска или шара.