5. Описание центробежного чувствительного элемента

В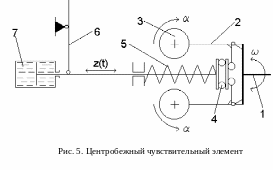 большинстве регуляторов частоты вращения вала судовых дизелей для контроля угловой скорости вала используются чувствительные элементы с грузами, расходящимися под воздействием центробежных сил. Такие чувствительные элементы могут иметь различную конструкцию, но принцип их действия одинаков.

На рис. 5 показана обобщенная схема центробежного чувствительного элемента для контроля угловой скорости. С валом дизеля 1 (или с валом привода ТНВД) шарнирно соединены рычаги 2 с грузами 3. При увеличении скорости вращения вала , под действием возрастающей центробежной силы, грузы 3 расходятся, поворачивая на угол  рычаги 2 и преодолевая сопротивление задающей пружины 5 через упорный подшипник 4. Изменением предварительного натяга пружины 5 можно изменять заданную скорость вращения валя дизеля.

Отклонение угловой скорости вала дизеля от заданной приводит к перемещению z(t) тяги чувствительного элемента. Зависимость z() при небольших изменениях скорости близка к линейной. Передача 6 передает перемещение тяги другим механизмам регулятора. Эта передача выполняется разными способами. Для успокоения (демпфирования) механизма чувствительного элемента в его состав вводится гидравлический демпфер 7 (катаракт). В изодромном регуляторе роль катаракта выполняет золотниковый гидрораспределитель

Линеаризованное дифференциальное уравнение чувствительного элемента можно записать в следующем виде

, (19)

где – масса подвижных частей чувствительного элемента, приведенная к его тяге (грузы, рычаги, выжимной подшипник и др.);  – коэффициент жидкостного сопротивления катаракта;  – жесткость задающей пружины, – перемещение тяги в абсолютных величинах.

Чтобы получить относительную величину перемещения, разделим уравнение на l_н, где l_н – полный рабочий ход тяги чувствительного элемента,

, (20)

где – относительное перемещение тяги чувствительного элемента, полному ходу рейки соответствует .

После преобразования уравнения к операторной форме записи, получим

, (21)

где , – постоянные времени чувствительного элемента; – коэффициент преобразования (усиления) чувствительного элемента.

На основе дифференциального уравнения определяем передаточную функцию чувствительного элемента:

, (22)

Эта передаточная функция соответствует передаточной функции типового колебательного звена. Отношение постоянных времени определит степень демпфирования звена и вид переходного процесса в нем.

По исходным данным для чувствительного элемента вычисляются его параметры. При вычислении коэффициента преобразования чувствительного элемента рассмотрим установившийся режим с , тогда (полагая в дифференциальном уравнении p = 0) получим:

, (23)

где z – относительная величина перемещения тяги чувствительного элемента;  – изменение угловой скорости, вызывающее перемещение z.

Для всережимного регулятора полное рабочее перемещение тяги чувствительного элемента (относительная величина z = 1) соответствует изменению угловой скорости вращения вала от _мин до _н, следовательно, для коэффициента преобразования можно записать:

. (24)