
4. Повторные независимые испытания. Теорема Бернулли
При решении задач теории вероятности часто возникают ситуации, в которых одно и тоже испытание повторяется многократно, причем исход каждого испытания независим от исходов других и наступает с одинаковой вероятностью. Такой эксперимент называютсхемой повторных независимых испытаний или схемой Бернулли.
Пусть
некоторое событие А наступает в каждом
испытании с вероятностью ![]() (вероятность
успеха). Обозначим за
(вероятность
успеха). Обозначим за ![]() вероятность
того, что событие А не наступит в испытании
(вероятность противоположного события,
неудачи). Произведем n независимых
испытаний. Тогда вероятность
вероятность
того, что событие А не наступит в испытании
(вероятность противоположного события,
неудачи). Произведем n независимых
испытаний. Тогда вероятность ![]() того,
что событие А в них наступило в точности
k раз, можно найти по формуле
Бернулли:
того,
что событие А в них наступило в точности
k раз, можно найти по формуле
Бернулли:
![]()
Вообще говоря, данную вероятность можно было вычислить непосредственно, используя теоремы сложения и умножения вероятностей. Но при достаточно большом количестве испытаний это трудоемкий путь. Формула Бернулли обобщает способ вычисления таких вероятностей и дает простой и удобный инструмент вычисления (Якоб Бернулли (1654 – 1705) – швейцарский математик).
Распределение числа успехов (появлений события А) носит название биномиального распределения.
Схема
Бернулли позволяет установить, какое
число появлений события А наиболее
вероятно. Формула для наивероятнейшего
числа появлений события
А имеет вид: ![]() .
При этом число
.
При этом число ![]() может
принимать либо одно значение
может
принимать либо одно значение ![]() (когда
является
целым числом), или два значения (когда
целым является
(когда
является
целым числом), или два значения (когда
целым является ![]() ).
).
Пример. Вероятность попадания в цель при одном выстреле равна 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах будет ровно 3 попадания в цель.
Решение. Подставляем
в формулу Бернулли данные задачи ![]() и
получаем:
и
получаем:
![]()
Пример. На склад из производственного цеха поступает в среднем 5% нестандартных деталей. Найти вероятность того, что среди взятых наудачу 10 деталей 2 будут нестандартными.
Решение. Событие
А - «появление нестандартной детали»,
его вероятность ![]() ,
число деталей
,
число деталей ![]() .
По формуле Бернулли находим для
.
По формуле Бернулли находим для ![]() :
:
![]()
5. Дискретные случайные величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:
X |
x1 |
x2 |
... |
xn |
P |
p1 |
p2 |
... |
pn |
Пример. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тыс. руб. и десять выигрышей по 1тыс. руб. Найти закон распределения случайных величин Х - стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: Напишем возможные значения х: х1=50, х2=1, х3=0. Вероятности этих возможных значений таковы: Р1=1/100=0,01, Р2=10/100=0,1, Р3=89/100=0,89. Напишем искомый закон распределения:
X |
50 |
1 |
0 |
P |
0.01 |
0.1 |
0.89 |
Контроль: 0,01+0,1+0,89=1.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина Х может принимать только значения х1, х2, х3,...,хn вероятности которых соответственно равны p1, p2, p3,...,pn. Тогда математическое ожидание М(х) случайной величины Х определяется равенством:
M(x)=х1p1+х2p2+...+хnpn
Если дискретная случайная величина Х принимает счетное множество возможных значений, то:
![]()
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Пример. Найти математическое ожидание случайной величины Х, зная закон ее распределения:
X |
3 |
5 |
2 |
P |
0.1 |
0.6 |
0.3 |
Решение: Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности: М(х)=3 .
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной М(С)=С. 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX)=CM(X) 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)•M(Y). 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: M(X+Y)=M(X)+M(Y).
Теорема. Математическое ожидание М(х) числа появлений событий А в n независимых испытаниях равно произведению этих испытаний на вероятность появления событий в каждом испытании: M(x) = np.
Пусть Х- случайная величина и М(Х) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность Х - М(Х).
Отклонением называют разность между случайной величиной и ее математическим ожиданием.
Отклонение имеет следующий закон распределения:
X-M(x) |
X1-M(x) |
X2-M(x) |
... |
Xn-M(x) |
P |
p1 |
p2 |
... |
pn |
Теорема. Математическое ожидание отклонения равно нулю: M(X-M(x)=0.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
D(x)=M[X-M(x)]2 (2)
Пример. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
X |
1 |
2 |
5 |
P |
0.3 |
0.5 |
0.2 |
Решение: Найдем математическое ожидание: [X1-M(x)]2=(1-2.3)2=1.69 [X2-M(x)]2=(2-2.3)2=0.09 [X3-M(x)]2=(5-2.3)2=7.29
Напишем закон распределения квадрата отклонения:
[X-M(x)]2 |
1.69 |
0.09 |
7.29 |
P |
0.3 |
0.5 |
0.2 |
По определению, D(x) = 1.69•0.3+0.09•0.5+7.29•0.2=2.01
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:
D(x)=M(x2)-[M(x)]2 (3)
Пример. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:
X |
2 |
3 |
5 |
P |
0.1 |
0.6 |
0.3 |
Решение: Найдем математическое ожидание М(х): M(x)=2•0.1+3•0.6+5•0.3=3.5
Напишем закон распределения случайной величины X2
X2 |
4 |
9 |
25 |
P |
0.1 |
0.6 |
0.3 |
Найдем математическое ожидание M(x2): M(x2) = 4•0.1+9•0.6+25•0.3=13.5
Искомая дисперсия D(x)=M(x2)-[M(x)]2=13.3-(3.5)2=1.05
Свойства дисперсии:
1. Дисперсия постоянной величины С равна нулю: D(C)=0 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. D(Cx)=C2D(x) 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. D(X1+X2+...+Xn)=D(X1)+D(X2)+...+D(Xn) 4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании D(X)=npq
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение.
Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии:
σ(X) = √D(X) (4)
Пример . Случайная величина Х задана законом распределения
X |
2 |
3 |
10 |
P |
0.1 |
0.4 |
0.5 |
Найти среднее квадратичное отклонение σ(x)
Решение: Найдем математическое ожидание Х: M(x)=2•0.1+3•0.4+10•0.5=6.4 Найдем математическое ожидание X2: M(x2)=22•0.1+32•0.4+102•0.5=54 Найдем дисперсию: D(x)=M(x2)=M(x2)-[M(x)]2=54-6.42=13.04 Искомое среднее квадратичное отклонение σ(X)=√D(X)=√13.04≈3.61
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратичных отклонений этих величин:
![]() (5)
(5)
Пример. На полке из 6 книг 3 книги по математике и 3 по физике. Выбирают наудачу три книги. Найти закон распределения числа книг по математике среди выбранных книг. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Введем
дискретную случайную величину X =
(Количество книг по математике среди 3
отобранных). X может
принимать значения 0, 1, 2 и 3. Найдем
соответствующие вероятности (по формуле
гипергеометрической вероятности).
X=0,
если все три книги – не по математике.
Вероятность 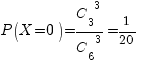 .
X=1,
если одна книга по математике и две –
не по математике. Вероятность
.
X=1,
если одна книга по математике и две –
не по математике. Вероятность 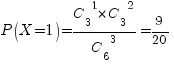 .
X=2,
если две книги по математике и одна нет.
Вероятность
.
X=2,
если две книги по математике и одна нет.
Вероятность 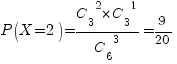 .
X=3,
если все три книги – по математике.
Вероятность
.
X=3,
если все три книги – по математике.
Вероятность 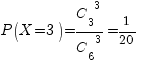 .
Получаем
закон распределения случайной
величины X:
xi
0 1 2 3
pi
1/20 9/20 9/20 1/20
Математическое
ожидание равно
.
Получаем
закон распределения случайной
величины X:
xi
0 1 2 3
pi
1/20 9/20 9/20 1/20
Математическое
ожидание равно
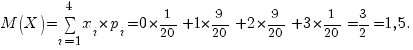
М(Х2) = 02*1/20 + 12*9/20 + 22*9/20 + 32*1/20 = 2,7
D(X)= М(Х2)- М(Х) 2= 2,7 – 1,52 = 0,45
