Методичка к контрольным работам.

1.Комбинаторика.

Рассмотрим некоторое множество Х, состоящее из n элементов  . Будем выбирать из этого множества различные упорядоченные подмножества Y из kэлементов.

Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор   элементов множества Х.

Если выбор элементов множества Y из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по kнаходится по формуле   (размещения с повторениями).

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается   и определяется равенством

Пример. Пусть даны цифры: 7; 8; 9; 4; 5; 6. Определить сколько двузначных чисел можно составить из этих цифр.

Решение. Если цифры могут повторяться, то количество двузначных чисел будет  . Если цифры не повторяются, то  .

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно  .

Пример. На библиотечной полке стоят 30 книг, причем 27 - книги разных авторов и еще 3 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?

Решение. Временно объединим три книги одного автора в один объект, всего получим 28 объектов - 27 книг и 1 объект из трех книг. Для них число перестановок будет  . Теперь три книги переставим между собой   способами. По правилу произведения получаем, что число способов расставить книги нужным образом равно: 

Пусть теперь из множества Х выбирается неупорядоченное подмножество Y (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по kназываются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается   (от начальной буквы французского слова "combinasion", что значит "сочетание") и равно .

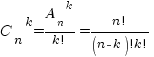Справедливы равенства: 

Пример. Учитель хочет назначить 3 человек для уборки класса из 27 учеников. Сколькими способами можно это сделать?

Решение. Так как порядок учеников не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27): 

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

2. Классическая вероятностная модель. Геометрическая вероятность

Основным понятием теории вероятностей является понятие случайного события. Случайное событие - это событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, выпадение двух гербов или герба и решки при бросании двух монет - это случайные события.

Сначала введем некоторые определения, касающиеся случайных событий: достоверные, невозможные, несовместные события.

Достоверное событие - то, которое в результате испытания обязательно происходит. Например, "выпадет или орел, или решка при бросании одной монеты".  Невозможное событие то, которое в результате испытания произойти не может. Например, "вытащен красный шар из ящика, в котором 3 белых и 3 черных шара". Несовместные случайные события - такие, что никакие два из них не могут появиться вместе в данном испытании. Например "выпадение герба" и "выпадение решки" при испытании, состоящем в бросании одной монеты

Случайные события образуют полную группу событий, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Таким образом, эти события покрывают все возможные исходы испытания.

Перейдем к определению классической вероятности. Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.

Пример. В мешке находится 10 пронумерованных бочонков (на каждом бочонке поставлено по одной цифре от 1 до 10). Бочонки с цифрами 1, 2, 3 и 4 - красные, остальные – черные. Появление бочонка с цифрой 1 (или цифрой 2, или цифрой 3, или цифрой 4) есть событие, благоприятствующее появлению красного бочонка. Появление бочонка с цифрой 4 (или цифрой 5, 6, 7, 8, 9, 10) есть событие, благоприятствующее появлению черного бочонка.

Вероятностью события A называют отношение числа благоприятствующих этому событию исходов m к общему числу всех равновозможных несовместных элементарных исходов n, образующих полную группу исходов:  . Это классическое определение вероятности.

Перечислим свойства вероятности: 1. Вероятность достоверного события равна единице 2. Вероятность невозможного события равна нулю. 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Таким образом, вероятность любого события удовлетворяет неравенству  .

Приведем несколько решений примеров на классическое определение вероятности.

Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 2?

Решение. Пусть событие А = (Номер вынутого бочонка не превосходит 2). Число случаев благоприятствующих появлению события А равно числу бочонков с номерами не более 2 (то есть 1 и 2), поэтому m=2. Общее число исходов n=10. Следовательно,  .

Пример. На входной двери имеется замок c 10 цифрами на кнопках. Для того, чтобы открыть замок, необходимо нажать три кнопки так, чтобы цифры на них составили определенное число. Найти вероятность того, что замок откроют с первой попытки.

Решение. Найдем вероятность этого события по классическому определению вероятности:  , где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных исходов. - число различных кодовых комбинаций (первая цифра любая от 0 до 9, вторая цифра любая от 0 до 9 и третья цифра любая от 0 до 9).  - только одна комбинация (число) верная.  Тогда вероятность открыть замок равна:  .

Не всегда бывает удобно для непосредственного подсчета вероятности использоватьклассическое определение вероятности (например, когда число исходов некоторого опыта бесконечно, как при выборе точки из отрезка и т.п.). Зачастую при этом используется другой метод - геометрический подход к определению вероятности.

Предположим, что случайное испытание можно представить как бросание произвольной точки наудачу в некоторую геометрическую область D (на прямой, плоскости или пространстве, в зависимости от задачи).  Элементарные исходы – это отдельные точки области D, любое событие – это некоторое подмножество этой области (фактически - пространства элементарных исходов). Можно считать, что все точки D "равноправны", и тогда вероятность попадания точки в некоторое подмножество этой области пропорциональна мере (длине, площади, объему) подмножества и не зависит от его расположения внутри области и формы. Таким образом приходим к геометрическому определению вероятности.

Геометрическая вероятность некоторого события А определяется формулой: 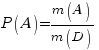 Здесь   – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и множества исходов, благоприятствующих осуществлению события А.

Пример. Мишень для выстрелов в тире представляет собой круг радиуса R. Стрелок выбивает 10 очков, если попадает в малый круг в центре с радиусом r,   Какова вероятность выбить 10 очков при одном выстреле?

Решение. Используем геометрическое определение вероятности. Множество всех элементарных исходов - мишень, круг радиуса R, его площадь равна  . Множество элементарных исходов, соответствующих событию "Выбито 10 очков" - это круг радиуса rего площадь равна  .

По геометрическому определению вероятности получаем, что искомая вероятность есть отношение площади малого круга, куда пуля должна попасть, к площади всей мишени - большого круга, то есть:  .

Пример. На плоскость, расчерченную параллельными полосками шириной в 2d (расстояние между осевыми линиями равно 2D), наудачу брошен круг радиуса r   Найти вероятность того, что данный круг пересечет некоторую полоску (линию).

Решение. Положим, что элементарный исход испытания - это расстояние x от центра круга до осевой линии ближайшей к кругу полоски. Тогда все пространство элементарных исходов – это отрезок  . Пересечение круга с полоской произойдет только в том случае, если его центр попадет в полосу, т.е.  , или будет находится от края полосы на расстоянии меньшем чем радиус, т.е.  .

По геометрическому определению вероятности получаем ответ:  .