3.4.3. Геометричний розрахунок зубчастих коліс

Під час виконання геометричного розрахунку необхідно визначити:

- ширину вінців зубчастих коліс;

- кут нахилу зубців косозубих коліс;

- кількості зубців зубчастих коліс;

- уточнену міжосьову віддаль;

- параметри корегування зубчастих коліс, якщо воно потрібне;

- діаметри всіх зубчастих коліс.

Робоча ширина вінців зубчастих коліс вибирається залежно від міжосьової віддалі за формулою

b = _bа a_= (0,18…0,24)a_ (3.5)

Ширина вінців визначає загальну ширину КП, яка лежить у межах (2,7...3,0)a_. Із зменшенням ширини вінців погіршуєть­ся плавність роботи і зростає шумність роботи косозубих коліс із-за зменшення коефіцієнта осьового перекриття. Спроба компенсувати змен­шення ширини збільшенням кута нахилу зубців для збереження коефіцієнта перекриття приводить до збільшення осьових сил у зачепленні, що нега­тивно впливає на роботу підшипників.

Кут нахилу зубців косозубих передач вибирають, враховуючи такі міркування:

1. Для забезпечення плавності роботи осьова ступінь перекриття зубців повинен бути не меншим від одиниці, тобто

, звідки .

2. Осьові сили, що діють від косозубих коліс на проміжний вал, повинні взаємно врівноважуватись, тобто :

де – осьова сила в парі постійного зачеплення;

– осьова сила у зачепленні коліс і-ї передачі;

Т_пр – крутний момент на проміжному валу.

Враховуючи це, отримаємо

де _пр, _i – кути нахилу зубців відповідно веденого колеса пари постійного зачеплення та веденого колеса і-ї передачі; r_пр, r_i – радіуси шестерні відповідно постійного зачеплення та і-ї передачі.

3. Шляхом зміни кута нахилу зубців можна змінити міжосьову віддаль

Змінюючи кути нахилу зубців відповідної пари зубчастих коліс, можна змінити міжосьову віддаль цієї пари і забезпечити вписування її в задану міжосьову віддаль без корегування.

Однак у більшості коробок передач всі зубчасті колеса мають однаковий кут нахилу зубців, що зумовлено деякими технологічними перевагами.

Кількість зубців ведучого колеса пари постійного зачеплення вибира­ють близьким до мінімального за умови відсутності підрізу зубців. Необхідно враховувати, що сума кількості зубців двох коліс у зачеп­ленні повинна бути непарною і кількість зубців коліс зубчастої пари не повинні бути кратними для запобігання нерівномірності зношення зубців.

За попередньо розрахованою міжосьовою віддаллю а_ і вибраному модулю m розраховують кількість зубців шестерні та веденого колеса всіх зубчастих пар за формулами:

• для прямозубої передачі ;

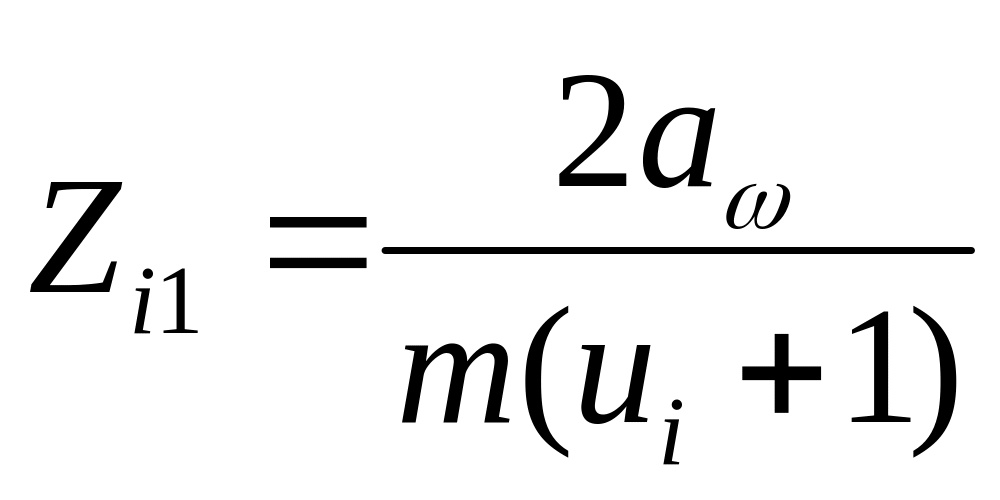• для косозубої передачі 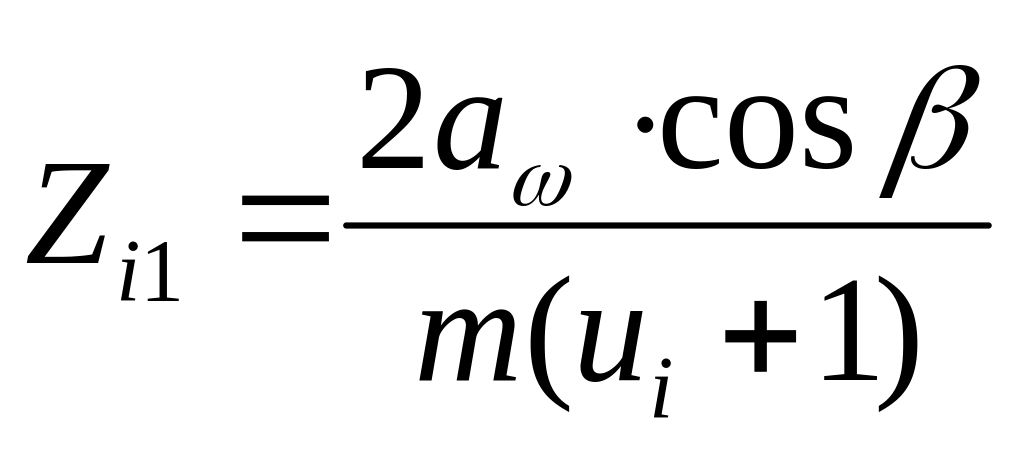; Z_i2 = Z_i1  u_i (3.6)

де u_i – передатне число зубчастої пари, що розраховується; u_i = u_ki – в двовальній коробці передач, – у тривальній коробці передач.

Одержані значення чисел зубців заокруглюють до цілих значень і по них коректують передатні числа.

За одержаним значенням кількостей зубців зубчастих пар уточнюють їх міжцентрові віддалі:

. (3.7)

У разі рівності розрахованих значень міжцентрових віддалей а_і = а_ кожна пара зубчастих коліс вписується в задану міжосьову віддаль. За відсутності такої рівності необхідно її забезпечити зміною кута нахилу зубців, що нетехнологічно, або шляхом кутового або висотного коригування.

Висотною називається корекція, за якої коефіцієнти зсуву головки та ніжки зубця рівні за величиною, але протилежні за знаком. Як правило Х₁ = -Х₂ = 0,125...0,325. Змінюється співвідношення між висотою головки та ніжки зубця при незмінній повній висоті зубця. Міжосьова віддаль і кут зачеплення залишається такими самими як і в некорегованому зачепленні. Висотна корекція застосовується для запобігання підрізу зубців і для підвищення їх міцності.

Кутовою називається корекція, за якої коефіцієнти зсуву голов­ки та ніжки зубця різні. Змінюється кут зачеплення. Застосовується вона для вписування зуб­частих коліс в задану міжосьову віддаль. За відсутності корекції  =20° і a_= mz/2.

Якщо задану пару зубчастих коліс необхідно вписати у міжосьову віддаль a_і, то новий кут зачеплення корегованих зубчастих коліс буде

.

Сумарний зсув інструменту не дорівнює нулю і визначається із залежності

,

де inv і inv_i – евольвентні функції кутів  і _i.

Розбивка Х_с на Х₁ і Х₂ здійснюється так:

де Х₁ , Х₂ – коефіцієнти зсуву відповідно головки та ніжки зубця; h_а – коефіцієнт висоти головки зубця, як правило h _а= 1; Z_min – мінімальна кількість зубців, що нарізується без корекції:

.

Крім того під час корекції також визначаються коефіцієнти сприятливого зміщення y та зрівнювального зміщення у за формулами

Наведені формули справедливі для прямозубого зачеплення. При косозубому зачепленні замість величин m, , _і потрібно брати аналогічні параметри у торцевому перетині.

Ділильні діаметри зубчастих коліс для косозубого зачеплення визначають за формулою

. (3.8)

Основні геометричні розміри зубчастих коліс визначають за формулами, наведеними в табл. 3.3. У цій таблиці індекс і = 1 відповідає ведучому колесу, індекс і = 2 – веденому.

Таблиця 3.3