Свойства определителей
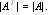 Определитель
не меняется при транспонировании
матрицы.
Определитель
не меняется при транспонировании
матрицы.
Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю.
При перестановке 2-х строк или столбцов матрицы определитель изменит знак на противоположный, сохраняя абсолютную величину.
Если матрица имеет две одинаковые строки или столбца, то определитель равен нулю.
Если все элементы какой-либо строки матрицы умножить на некоторое число ?, то определитель умножится на ?.
Если элементы двух строк(столбцов) матрицы пропорциональны, то ее определитель равен нулю.
Если все элементы какой–либо строки или столбца матрицы представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,
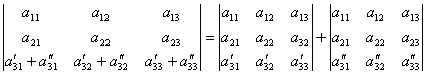
Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.
Общий множитель строки или столбца можно выносить за знак определителя. Например,
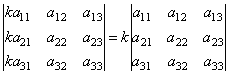
Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки(столбца) этой матрицы равна 0, т.е.
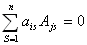
, при
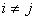
Сумма произведений произвольных чисел
 на
алгебраические дополнения элементов
любой строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на
числа
на
алгебраические дополнения элементов
любой строки (столбца) равна определителю
матрицы, полученной из данной заменой
элементов этой строки (столбца) на
числа
Определитель произведения двух квадратных матриц равен произведению их определителей:
-
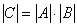
, где
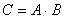
,А и В – матрицы n-го порядка.
Перечисленные свойства определителей позволяют существенно упростить их вычисления, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью этих свойств, чтобы преобразованная матрица имела строку (или столбец), содержащий как можно больше нулей, а потом найти определитель по этой строке (столбцу).
1.4 Обратная матрица
Для каждого числа
![]() существует
обратное число
существует
обратное число![]() такое,
что произведение
такое,
что произведение
![]() Для
квадратных матриц тоже вводится
аналогичное понятие.
Для
квадратных матриц тоже вводится
аналогичное понятие.
Определение.Матрица![]() называется
обратной по отношению к квадратной
матрице А, если при умножении этой
матрицы на данную как справа, так и слева
получается единичная матрица:
называется
обратной по отношению к квадратной
матрице А, если при умножении этой
матрицы на данную как справа, так и слева
получается единичная матрица:
-
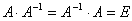
(1.10)
Из определения следует, что только квадратная матрица имеет обратную.
Однако не каждая квадратная матрица
имеет обратную; для существования
матрицы
необходимым
и достаточным условием является
требование
![]() .
.
Если определитель матрицы отличен от нуля ( ), то такая квадратная матрица называется невырожденной, или неособенной; в противном случае – вырожденной, или особенной.
Справедлива следующая теорема:
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.
Доказательство:
Необходимость. Пусть для матрицы A существует обратная матрица , т.е. .Покажем, что
Предположим, что
![]() По
свойству 12(
По
свойству 12(![]() )определителей
имеем
)определителей
имеем
![]() .
Но с другой стороны
.
Но с другой стороны
![]() .
.
Полученное противоречие доказывает, что
Достаточность. Для простоты
доказательство проведём для случая
матрицы третьего порядка. Пусть и
.
и
.
Покажем, что в этом случае обратной
матрицей будет матрица
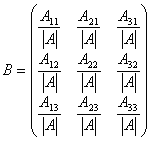 ,
где
,
где![]() алгебраическое
дополнение элемента
алгебраическое
дополнение элемента
![]() .
.
Найдём AB=C.
Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,
![]()
Аналогично по теореме о разложении
определителя по элементам строки можно
доказать, что
![]()
Кроме того, все недиагональные элементы матрицы C равны нулю.
Например,
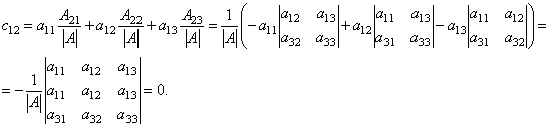
Следовательно, AB=E. Аналогично можно показать, что BA=E.
Поэтому![]()
Таким образом, теорема содержит способ нахождения обратной матрицы. Если условия теоремы выполнены, то матрица обратная к матрице
находится следующим образом
-
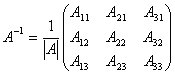
(1.11)
где алгебраическое дополнение элемента данной матрицы A.
Введем понятие присоединенной матрицы.
Присоединенной называется матрица,
элементы которой являются алгебраическими
дополнениями элементов матрицы
![]() ,
транспонированной к А :
,
транспонированной к А :![]() (i
= 1,2,…,n; j = 1,2,…, n).
(i
= 1,2,…,n; j = 1,2,…, n).
Тогда формулу (1.9) можно представить в виде
-
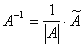 (
)
(
)(1.12)
Алгоритм вычисления обратной матрицы:
Найти определитель матрицы A. Если , то матрица А – вырожденная и обратной матрицы не существует. Если , то матрица А – невырожденная и обратная матрица существует.
Найти транспонированную матрицу .
Найти алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу .
Вычисляем обратную матрицу по формуле (1.10)
Проверить правильность вычисления обратной матрицы, исходя из ее определения (этот пункт не обязателен).
Вычисление обратной матрицы по формуле (1.12) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример.
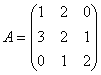 .
Найдем обратную матрицу.
.
Найдем обратную матрицу.