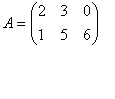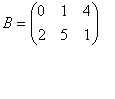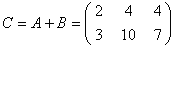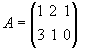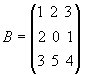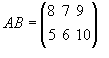Лекционные материалы Основные сведения о матрицах

Прямоугольной матрицей размера называется совокупность чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

(1.1)

или сокращенно в виде . Числа , составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы и одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если . Матрица, состоящая из одной строки или одного столбца, называется соответственно вектор-строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами. Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера , все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:

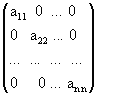
Если все элементы диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю.

1.2 Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.

1. Умножение матрицы на число. Произведением матрицы А на число называется матрица B= А, элементы которой получаются из соответствующих элементов матрицы А умножением на число : для i =1,2,… m; j =1,2…,n.

Например, если

,то

.

Следствия.

1. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

2. Произведение матрицы А на число 0 есть нулевая матрица, т.е. 0•А=0

2. Сложение матриц. Суммой двух матриц одинакового размера называется матрица того же размера, элементы которой определяются по формуле для i =1,2,… m; j =1,2…,n.

Например,

В частном случае А + 0 = А.

3. Вычитание матриц.Разность двух матриц одинакового размера определяется через предыдущие операции:

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу второй. В этом случае матрица А называется согласованной с матрицей В. Произведением двух матриц , где i =1,2…,n; j=1,2…,m; k=1,2…,p, называется матрица , элементы которой определяются по следующему правилу:

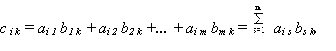
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Например,

и

Матрица А размера , матрица В размера , тогда произведение АВ = С существует и элементы матрицы С равны

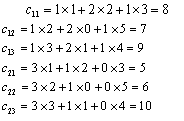
, а произведение BA не существует.

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из определений этих операций):

1. А+В = В+А

2. (А+В)+С = А+(В+С)

3. ?(А+В) = А + В

4. А(В+С) = АВ + АС

5. (А+В)С = АС + ВС

6. ?(АВ) = ( А)В = А( В)

7. А(ВС) = (АВ)С

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

• Если произведение матриц АВ существует, то после перестановки множителей местами произведения матриц ВА может и не существовать, если число столбцов первой матрицы не совпадает с числом строк второй матрицы.

• Если даже произведения АВ и ВА существуют, то они могут быть матрицами разных размеров.

• В случае, когда оба произведения АВ и ВА существуют и оба – матрицы одинакового размера (это возможно только при умножении квадратных матриц А и В одного порядка), коммутативный (переместительный) закон умножения не выполняется, т.е. А•В ? В•А. В частном случае коммутативным законом обладает произведение любой квадратной матрицы А n-ого порядка на единичную матрицу Е того же порядка, причем это произведение равно А: АЕ = ЕА = А.

• Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что А•В = 0, не следует, что А=0, или В=0.

Например,

;

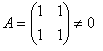
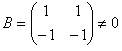
, но

.
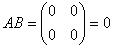
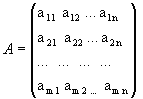
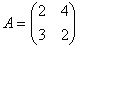