1.2. Робота компресора при різноманітних термодинамічних процесах стискання

Аналіз виразів (1.7) і (1.9) показує, що робота теоретичного компресора визначається такими чинниками: 1) розмірами початкового і кінцевого тисків p₁ і р₂; 2) термодинамічними властивостями середовища, яке стискається; 3) термодинамічним характером процесу стискання.

Роздивимося вплив на роботу компресора характеру процесу стискання. Для інтегрування виразу (1.7) необхідно знати аналітичну залежність між тиском і питомим об’ємом у процесі стискання за постійної маси робочої речовини. Зв’язок між цими величинами для будь-якого термодинамічного процесу стискання виражається рівнянням

, (1.10)

де n - показник політропи процесу стискання.

Залежно від термодинамічного характеру розрізняють ізотермічний, адіабатний і політропний процеси стискання.

Ізотермічний процес стискання відбувається за постійної початкової температури Т₁=const. Оборотний ізотермічний процес потребує для свого здійснення відведення теплоти від середовища, яке стискається, до зовнішнього джерела з температурою Т₁. Показник ізотерми визначається виразом .

При стисканні ідеального газу , і робота компресора дорівнює роботі стискання, тобто

. (1.11)

Інтегруючи вираз (1.11) із використанням рівняння стану для ідеального газу , отримаємо

(1.12)

У індикаторній діаграмі (рис.1.1) ізотерма 1-5 має найбільш пологий характер, тому робота компресора буде найменшою.

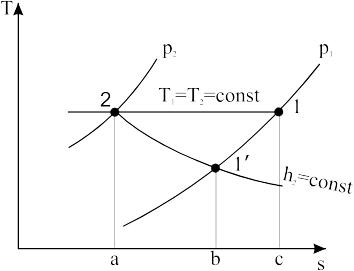
Рис.1.2. Робота компресора при ізотермічному процесі стискання

Вираз (1.9) дозволяє проаналізувати роботу компресора в термодинамічних діаграмах стану, наприклад у координатах s-Т – рис.1.2. Відзначимо, що процеси всмоктування і нагнітання в діаграмах стану зобразити неможливо, тому що вони проходять із перемінною масою і за постійних тиску і температури. На рисунку різниця ентальпій h₂-h₁ еквівалентна площі 1-1'-b-с, що виражає кількість теплоти в ізобарному процесі 1-1'. Другий член рівняння (1.9) для ізотермічного стискання буде мати вигляд: , він чисельно еквівалентний площі 1-2-а-с. З урахуванням знаків обох членів рівняння (1.9) робота компресора еквівалентна площі 1-2-а-b-1'. Для ідеального газу лінія постійної ентальпії збігається з ізотермою і робота компресора буде виражатися площею 1-2-а-с, тобто зросте на величину площі під процесом 1-1'.

А діабатний процес стискання в компресорі відбувається без теплообміну з зовнішніми джерелами теплоти, тобто для такого процесу . Оборотний адіабатний процес є ізоентропним, тому що для нього справедливі рівності і . Показник ізоентропи процесу є величиною перемінною, тому в практичних розрахунках часто використовують його середнє значення в заданому інтервалі зміни параметрів стану середовища, яке стискається. У цьому випадку інтегрування виразу (1.11) призводить до результату

, (1.13)

або для ідеального газу

. (1.14)

Інший вираз для адіабатної роботи компресора випливає з рівності (1.9)

. (1.15)

Ця робота еквівалентна площі 2-2'-b-c на рис.1.3 для реального газу і збільшується на величину площі під процесом 2'-3 для ідеального газу.

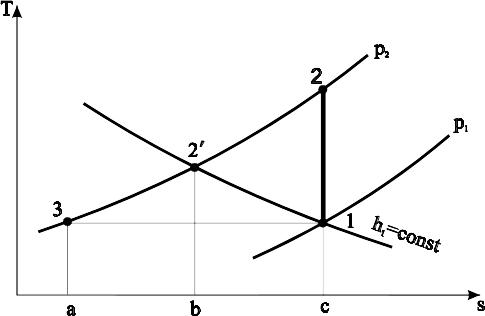
Рис.1.3. Робота компресора при ізоентропійному процесі стискання

Робота компресора при політропному процесі стискання визначається виразом (1.13), у який замість показника адіабати k входить показник політропи n. При відведенні теплоти від середовища, яке стискається, до зовнішнього джерела буде мати місце співвідношення і процес стискання відхиляється уліво від адіабати - лінія 1-2' на рис.1.4. У цьому випадку обидва члени правої частини рівності (1.9) позитивні і виражаються відповідно площами 2'-3-а-b і 1-2'-b-с, а робота еквівалентна площі 1-2'-3-а-с. На практиці процес стискання з відведенням теплоти має місце в компресорах із водяним чи повітряним охолодженням циліндра, а також у мастилонаповнених компресорах.

При підведенні теплоти ззовні процес стискання відхиляється управо від адіабати – лінія 1-2 на рис.1.4. Тут для одержання роботи компресора з площі 2-3-а-d, яка відповідає різниці ентальпій h₂-h₁ варто відняти площу 2-1-с-d, що відповідає кількості підведеної теплоти.

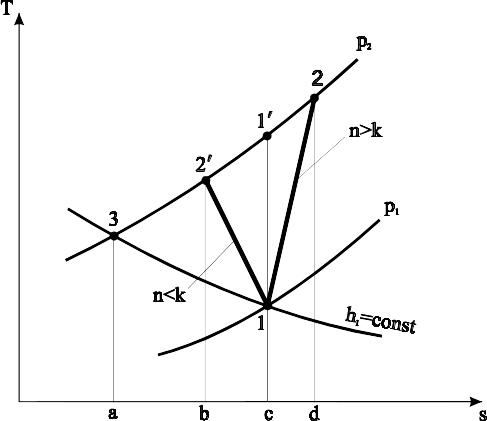
Рис.1.4. Робота компресора при політропному процесі стискання

У результаті одержимо площу 2-3-а-с-1, із чого можна зробити висновок, що підведення теплоти позбавлена практичного змісту, тому що крім витрати теплоти збільшується і робота стискання порівняно з адіабатним процесом.

На практиці процес стискання може відхилятися управо від адіабати по іншій причині – від внутрішнього тертя середовища, яке стискається, тертя середовища об елементи конструкції компресора та тертя деталей компресора між собою. На подолання цього тертя витрачається додаткова енергія, що у кінцевому рахунку перетворюється в теплоту, яка поглинається середовищем, яке стискається. У цьому випадку робота компресора виражається площею 2-3-а-d.