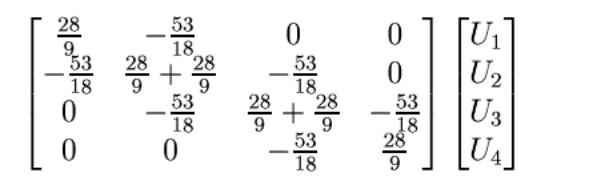- •1. Математическое моделирование и процесс создания математической модели
- •1.1 Процесс создания вычислительной модели
- •1.2. Вычислительный эксперимент
- •2. Погрешности численного решения задачи на эвм
- •2.1. Источники погрешностей
- •2.2. Качественная характеристика физических величин. Приближенные числа. Абсолютная и относительная погрешности измерения и вычисления
- •2.3. Погрешности арифметических операций
- •2.4. Корректность вычислительной задачи
- •3. Построение и исследование разностных схем для численного решения дифференциальных
- •1. Сетки и сеточные функции.
- •3.2. Основные определения
- •3. 3. Разностная аппроксимация дифференциальных операторов
- •4. Аналитическое решение и исследование свойств нелинейных колебательных систем
- •4.1. Постановка задачи Коши
- •4.3. Аналитическое исследование качественного поведения задачи Коши
- •5. Исследование нелинейных колебательных систем с помощью вычислительного эксперимента
- •5.1. Метод эйлера
- •5.2 Метод рунге-кутта.
- •5.3. Линейные многошаговые методы. Метод адамса.
- •8. Моделирование процесса распространения тепла
- •8.1. Уравнение теплопроводности и граничные условия
- •8.2. Решение одномерного уравнения теплопроводности
- •9. Численное моделирование краевых задач описывающих распространение тепла
- •9.1. Численное моделирование краевых задач описывающих стационарное распределение тепла
- •9.2. . Численное моделирование нестационарных краевых задач
- •Рассмотрим одномерную нестационарную смешанную краевую задачу
- •10. Исследование устойчивости разностных схем
- •10.1. Спектральный метод исследования устойчивости задачи Коши
- •11. Метод конечных элементов
- •11.3. Понятие о проекционном методе Галеркина
- •11.4. Понятие о проекционно-разностном методе конечных элементов
- •12. Понятие схем расщепления. Схема переменных направлений.
- •13. Программные реализации метода конечных элементов
- •Дополнительная литература
- •"Математическое моделирование физических процессов" в авторской редакции
- •Отпечатано на ризографе Издательства ИжГту
- •426069, Г. Ижевск, Студенческая, 7
11. Метод конечных элементов
11. 1. Метод взвешенных невязок и переход к методу конечных элементов.
Метод конечных элементов (МКЭ) – численный метод решения задач прикладной механики.
Широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электромагнитных полей. С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения. Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах (идея МКЭ была разработана советскими учёными ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развитие). Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать, как один из вариантов распространённого в строительной механике метода Рэлея-Ритца, который путём минимизации потенциальной энергии сводит задачу к системе дифференциальных уравнений или систем дифференциальных уравнений. линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина, или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения.
С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. Практически все современные расчёты на прочность проводят, используя метод конечных элементов.
Метод конечных элементов (МКЭ) является сеточным методом, предназначенным для решения задач микроуровня, для которого модель объекта задается системой дифференциальных уравнений в частных производных с заданными краевыми условиями
![]() ,
,
![]() (11.1)
(11.1)
Здесь L - дифференциальный оператор (например, оператор Лапласа),
u – фазовая переменная (решение - неизвестная функция, которую следует найти), f – правая часть (величина, независящая от u), – граничное условие первого рода (Дирихле), то есть на границе Г задано значение фазовой переменной.
Будем искать решение с помощью функции, имеющей следующий вид:
![]() (11.2)
(11.2)
Здесь
u*
- приближенное решение,
![]() - пробные функции,
- пробные функции,
![]() – неизвестные коэффициенты, которые
необходимо отыскать из условия наилучшего
удовлетворения дифференциальному
оператору, M- количество пробных функций.
Если подставить u*
дифференциальный оператор L,
то получим невязку, принимающую в
различных точках области разное значение
– неизвестные коэффициенты, которые
необходимо отыскать из условия наилучшего
удовлетворения дифференциальному
оператору, M- количество пробных функций.
Если подставить u*
дифференциальный оператор L,
то получим невязку, принимающую в
различных точках области разное значение
![]() (11.3)
(11.3)
Необходимо сформулировать условие, позволяющее минимизировать эту невязку по всей области. Одним из вариантов такого условия может быть следующее уравнение:
![]() (11.4)
(11.4)
Здесь
![]() - некоторые весовые функции, в зависимости,
от выбора которых различают варианты
метода взвешенных невязок, S- область
пространства, в которой ищется решение.
- некоторые весовые функции, в зависимости,
от выбора которых различают варианты
метода взвешенных невязок, S- область
пространства, в которой ищется решение.
При
выборе в качестве весовых функций дельта
- функций будем иметь метод, который
получил название метод поточечной
коллокации, для кусочно-постоянных
функций - метод коллокации по подобластям,
но наиболее распространенным является
метод Галеркина, в котором в качестве
весовых функций выбираются пробные
функции
.
В этом случае, если количество пробных
функций равно количеству весовых
функций, после раскрытия определенных
интегралов приходим к замкнутой системе
алгебраических уравнений относительно
коэффициентов A
![]() ,
где коэффициенты матрицы K и вектора Q
вычисляются по формулам:
,
где коэффициенты матрицы K и вектора Q
вычисляются по формулам:
![]() (11.5)
(11.5)
После нахождения коэффициентов A и подстановки их в (11.2), получаем решение исходной задачи.
Недостатки метода взвешенных невязок очевидны: поскольку решение ищется сразу по всей области, то количество пробных и весовых функций должно быть значительным для обеспечения приемлемой точности, но при этом возникают трудности при вычислении коэффициентов Kij и Qi, особенно при решении плоских и объемных задач, когда потребуется вычисление двойных и тройных интегралов по областям с криволинейными границами. Поэтому на практике этот метод не использовался, пока не был изобретен метод конечных элементов (МКЭ).
Идея метода заключается в следующем: в методе взвешенных невязок воспользоваться простыми пробными и весовыми функциями, но не во всей области S, а ее отдельных подобластях (конечных элементах), а точность решения задачи обеспечить использованием большого числа конечных элементов (КЭ), при этом КЭ могут быть простой формы и вычисление интегралов по ним не должно вызывать особых затруднений.
Математически переход от метода взвешенных невязок к МКЭ осуществляется с использованием специальных пробных функций, которые также называются глобальными базисными функциями, обладающих следующими свойствами:
1) в узле аппроксимации функции имеют значение равное единице;
2) отличны от нуля только в КЭ, содержащих этот узел аппроксимации, во всей остальной области равны нулю.
11.2. Решение одномерной стационарной задачи теплопроводности методом конечных элементов
В качестве первого примера применения метода конечных элементов рассмотрим решение одномерной стационарной задачи теплопроводности. Распределение температуры вдоль одномерной проводящей балки можно
описать уравнением:
![]() (11.6)
(11.6)
Здесь u температура, q(u, x) – утечка тепла, k – теплопроводность. Рассмотрим в качестве примера линейный случай q(u, x)=u. Тогда уравнение (11.6) примет вид:
![]() (11.7)
(11.7)
Предположим,
что граничные условия имеют вид:
![]() .
.
Это уравнение при k = 1 имеет точное решение равное:
![]() (11.8)
(11.8)
Это решение можно сравнить с приближенным решением, полученным методом конечных элементов. Чтобы решить рассматриваемое уравнение методом конечных элементов мы должны проделать следующее:
1. Записать уравнение теплопроводности в интегральном виде.
2. Проинтегрировать по частям (в одномерном случае) или с использованием теоремы Грина (в двумерном или трехмерном случае) чтобы уменьшить порядок производных.
3. Ввести конечно-элементную аппроксимацию для температурного поля, используя параметры узлов и базисные функции конечных элементов.
4. Проинтегрировать по элементам и вычислить матрицы нагрузки элементов и векторы правой части.
5. Путем ансамблирования получить глобальные линейные алгебраические уравнения.
6. Записать граничные условия.
7. Решить глобальные уравнения.
8. Оценить потоки тепла и распределение температуры.
Этапы решения перечисленных задач с общих позиций:
Выбор конечного элемента. В одномерной задаче это просто отрезок прямой. В двумерной задаче - треугольный (симплекс) элемент, четырёхугольный элемент, в общем случае любая фигура, с помощью которой можно разбить исследуемую область на непересекающиеся подобласти, но при этом следует учитывать, что чем сложнее элемент, тем с большими сложностями придётся столкнуться при вычислении интегралов, поэтому наиболее распространенными являются треугольный элемент и четырёхугольный со сторонами параллельными осям координат. Для трёхмерной области - тетраэдр и параллелепипед.
Разбиение области на КЭ. В отличие от метода конечных разностей разбиение может быть неравномерным и априорно учитывать градиент фазовой переменной, то есть там, где предполагается быстрое изменение фазовой переменной, сетка должна быть гуще и наоборот. Существуют различные способы автоматического разбиения области на конечные элементы, поскольку исполнение этого этапа вручную утомительно и часто приводит к ошибкам.
Получение функции формы. В зависимости от соотношения требований точности задачи и возможностей вычислительной системы выбирают линейную, квадратичную или более высокую степень функции формы, при этом число узлов аппроксимации должно быть минимум на единицу больше порядка аппроксимирующей функции.
Получение матрицы жёсткости и вектора нагрузок. Этот этап получил своё название из строительной механики, поскольку именно там впервые был применён МКЭ. На этом этапе используется метод взвешенных невязок в пределах одного КЭ.
Ансамблирование или получение глобальных матрицы жёсткости и вектора нагрузок.
Решение системы алгебраических уравнений. При решении может быть учтена особенность матрицы коэффициентов, поскольку она, как правило, имеет ленточную форму.
Рассмотрим перечисленные выше шаги.
Интегральное уравнение. Составим интегральное уравнение, используя метод взвешенных невязок (невязка ортогональна весовой функции W)
![]() (11.9)
(11.9)
Здесь
![]() – невязка, а W
– весовая функция
– невязка, а W
– весовая функция
![]() .
(11.10)
.
(11.10)
Если u* точное решение уравнения во всей области, то невязка равна нулю во всей области. Подставим выражение для невязки в интегральное уравнение (11.10)
![]() .
(11.11)
.
(11.11)
Полученное
интегральное уравнение показывает, что
невязка (или ошибка) стремится к нулю в
среднем по пространству; W
– выбирается так, что невязка ортогональна
к пространству функций
![]() ,
используемых в качестве аппроксимации
точного решения u.
,
используемых в качестве аппроксимации
точного решения u.
Интегрирование по частям. Большое преимущество решения задачи путем решения интегрального уравнения состоит в возможности понижения порядка производных при помощи интегрирования по частям (в случае двумерной и трехмерной задач при помощи использования теоремы Грина). Использование формулы интегрирования по частям дает:
![]() (11.12)
(11.12)
В результате интегральное уравнение (11.11) примет вид:
![]() .
(11.13)
.
(11.13)
Аппроксимация конечными элементами. Разделим область 0<x<1 на три элемента равной длины и заменим u(x) внутри каждого элемента при помощи конечно-элементной аппроксимации. Для нашей одномерной задачи набор кусочно-линейных функций, при количестве КЭ, равном трем, иллюстрируется следующим рис. 9.
В
результате
на каждом КЭ действует строго определенное
число ненулевых глобальных базисных
функций и вместо вычисления интеграла
по всей области можно вычислить интегралы
по КЭ и сложить их. Процедура сложения
получила название ансамблирование.
Использование глобальных базисных
функций приводит к тому, что процедура
вычисления интегралов по КЭ становится
достаточно простой и, поскольку в узлах
сетки
![]() ,
коэффициенты
А
приобретают
физический смысл, они становятся равными
значению фазовой переменной в узлах
сетки.
,
коэффициенты
А
приобретают
физический смысл, они становятся равными
значению фазовой переменной в узлах
сетки.
В
пределах одного КЭ, при условии, что он
включен между
![]() -
м
и
-
м
и
![]() -м
или i-м
и
-м
или i-м
и
![]() -м
узлами, кусочно-линейную аппроксимацию
решения можно определить с помощью
глобальных базисных функций следующим
образом:
-м
узлами, кусочно-линейную аппроксимацию
решения можно определить с помощью
глобальных базисных функций следующим
образом:
![]() (11.14)
(11.14)
а
аппроксимацию решения на всем интервале
![]() виде скалярного произведения
виде скалярного произведения
![]() .
.
Здесь
x*
- текущая
координата, отсчитываемая от начала
КЭ, l
- его длина,
![]() и
и
![]() - значения решения в узлах сетки,
- значения решения в узлах сетки,
![]() -
вектор приближенного решения уравнения
в узлах сетки, компоненты
вектора
-
вектор приближенного решения уравнения
в узлах сетки, компоненты
вектора
![]() получили
название функций формы конечного
элемента.
получили
название функций формы конечного
элемента.
Функции формы конечного элемента (компоненты вектора ), согласно (11.14), и их производные по x на равномерной сетке при кусочно-линейной аппроксимации имеют вид
![]() (11.15)
(11.15)
где
![]() - координаты узлов равномерной сетки,
- координаты узлов равномерной сетки,
![]() - шаг сетки равен длине конечного
элемента.
- шаг сетки равен длине конечного
элемента.
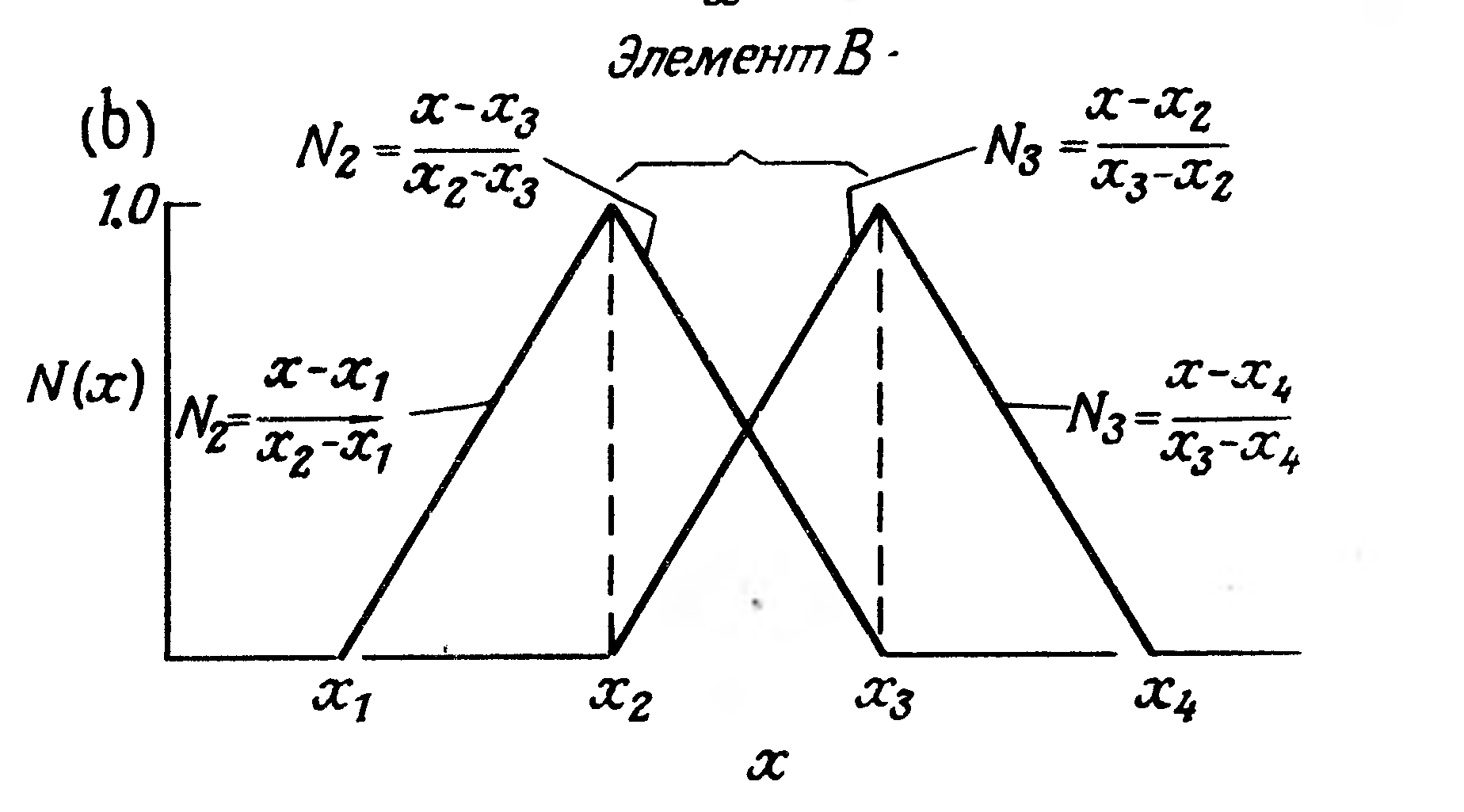
Рис. 8. Функции формы для кусочно-линейной аппроксимации.
Функции
формы можно получить и из других
соображений. Зададимся полиномом,
аппроксимирующим решение внутри
конечного элемента, например, линейным:
![]() .
При
.
При
![]()
![]() ,
при
,
при
![]()
![]() ,
отсюда находим коэффициенты
,
отсюда находим коэффициенты
![]() и подставляем их в линейную аппроксимацию
и получаем известное выражение (11.14)
и подставляем их в линейную аппроксимацию
и получаем известное выражение (11.14)
![]() .
.
Таким же образом можно получить функции формы для квадратичной, кубической и других аппроксимаций решения на КЭ. Соответственно аппроксимации и функции формы и КЭ называются - квадратичным, кубическим и т.д.
Например, получение квадратичной функции формы выглядит следующим образом. При этом, естественно, в пределах одного конечного элемента должно использоваться три узла сетки аппроксимации, один из которых является внутренним для КЭ. При расположении внутреннего узла сетки в середине КЭ (что необязательно) полином, аппроксимирующей решение внутри конечного элемента, будет иметь вид:
![]() (11.16)
(11.16)
При
![]()
![]() ,
при
,
при
![]()
![]() ,
при
,
при
![]()
![]() ,
где x*
- текущая
координата, отсчитываемая от начала
КЭ,
,
где x*
- текущая
координата, отсчитываемая от начала
КЭ,
![]() – длина конечного элемента, равная двум
шагам сетки.
– длина конечного элемента, равная двум
шагам сетки.
Решая
эту систему относительно коэффициентов
![]() ,
получим:
,
получим:
![]() .
.
Подставляя полученные коэффициенты в аппроксимацию (11.16), получим
![]() (11.17)
(11.17)
Используя формулу (11.17) можно построить функции формы для случая квадратичной аппроксимации, которые показаны на рис. 9
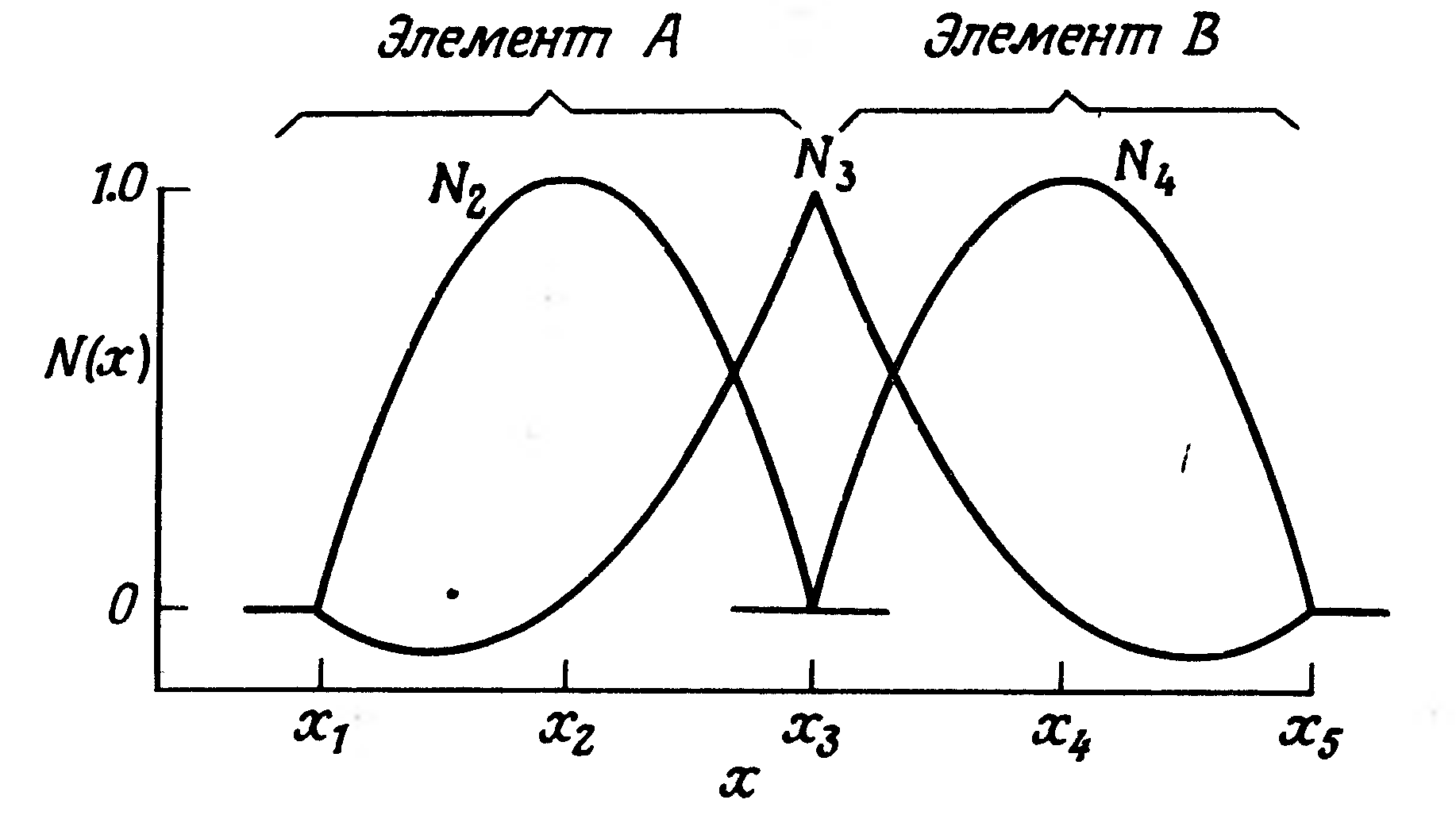
Рис.9. Функции формы для квадратичной аппроксимации.
Пример
построения функций формы
![]() для
квадратичной аппроксимации. Представим
для
квадратичной аппроксимации. Представим
![]() .
Тогда надо потребовать
.
Тогда надо потребовать
![]() ,
,
![]()
Интегралы
по элементам. Так
как
![]() и
и
![]() ,
то интегралы
в левой части уравнения (11.11) имеют вид,
,
то интегралы
в левой части уравнения (11.11) имеют вид,
![]() (11.18)
(11.18)
Элемент
матрицы
![]() ,
на который умножается приближенное
решение
в
узле сетки, называется элементом матрицы
жесткости
,
на который умножается приближенное
решение
в
узле сетки, называется элементом матрицы
жесткости
![]() (11.19)
(11.19)
Вычислим
элементы матрицы жесткости при длине
КЭ в нашем случае
![]()
![]() (11.20)
(11.20)
и аналогично
![]() (11.21)
(11.21)
Заметим, что матрица жесткости симметрична.
Анссамблирование. Процесс анссамблирования и функции формы при кусочно-линейной аппроксимации показаны на рис. 10.
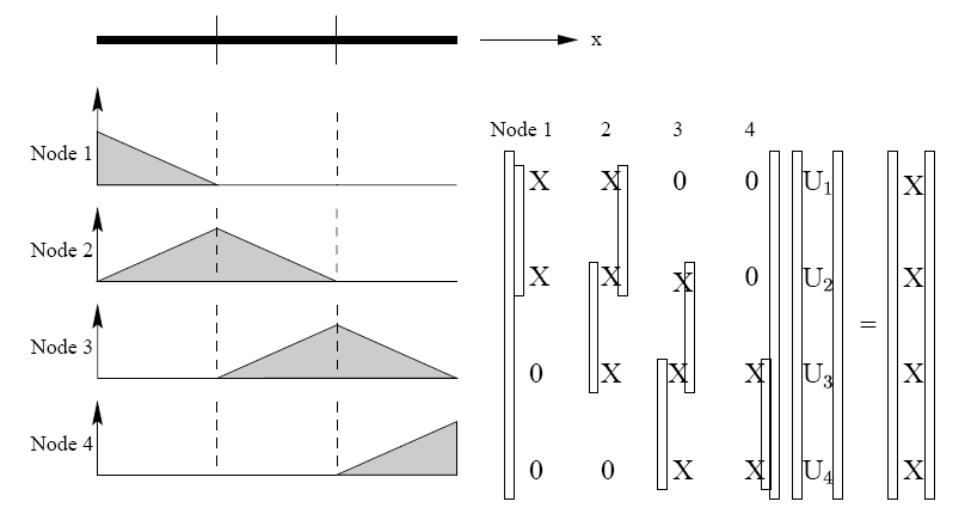
Рис.10. Процесс анссамблирования
Глобальное
матричное уравнение для решения задачи
при
![]() имеет
вид
имеет
вид