Нуль-граф и полный граф

Существуют некоторые специальные графы, встречающиеся во многих приложениях теории графов. Будем пока опять рассматривать граф как наглядную схему, иллюстрирующую ход спортивных состязаний. До начала сезона, пока еще никакие игры не проводились, на графе нет никаких ребер. Такой граф состоит из одних изолированных вершин, т. е. из вершин, не соединенных никакими ребрами. Граф такого вида называется нуль-графом. На рис. 3 приведены такие графы для случаев, когда число команд, или вершин, равно 1, 2, 3, 4 и 5. Эти нуль-графы обычно обозначаются символами O₁, O₂, O₃ и т. д., так что O_n – это нуль-граф с n вершинами, не имеющий ребер.

Рассмотрим другой крайний случай. Предположим, что по окончании сезона каждая команда сыграла по одному разу с каждой из остальных команд. Тогда на соответствующем графе каждая пара вершин будет соединена ребром. Такой граф называется полным графом. На рис. 4 изображены полные графы с числом вершин n = l, 2, 3, 4, 5.

Рис. 3. Нуль-графы для различного числа команд: 1,2,3,4 и 5

Рис. 4. Полные графы для различного числа команд: 1,2,3,4 и 5

Обозначим эти полные графы соответственно через U₁, U₂, U₃, U₄, U₅, так что граф U_n состоит из n вершин и ребер, соединяющих все возможные пары этих вершин. Этот граф можно представлять себе как n -угольник, в котором проведены все диагонали.

Имея некоторый граф, например граф G, изображенный на рис. 1, всегда можно превратить его в полный граф с теми же самыми вершинами, добавив недостающие ребра (т. е. ребра, соответствующие играм, которые только еще будут сыграны). На рис. 5 это сделано для графа, представленного на рис. 1 (еще не состоявшиеся игры изображены пунктиром).

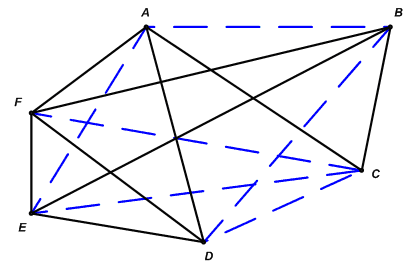
Рис. 5. Граф с рис. 1, дополненный ребрами до полного графа

Можно также отдельно начертить граф, соответствующий пока еще не сыгранным, будущим играм. Для графа G при этом получится граф, изображенный на рис. 6.

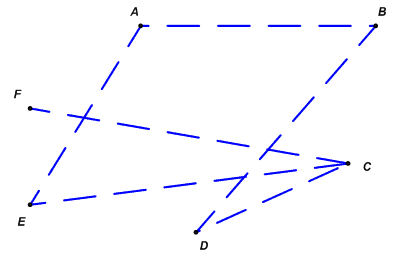
Рис. 6. Граф , являющийся дополнением графа G с рис. 1 до полного графа

Этот новый граф называется дополнением графа G; принято обозначать его через . Взяв дополнение графа , мы снова получим граф G. Ребра обоих графов G и вместе составляют полный граф с теми же вершинами.

Упражнения

1. Начертите дополнение графа, изображенного на рис. 2.

2. Чему равно число ребер полного графа U_n?

Изоморфные графы

Граф G (рис. 1) можно изображать по-разному. Во-первых, не обязательно изображать его ребра прямолинейными. Можно провести любые линии, соединяющие те же самые вершины, что и раньше, так что граф G можно представить в виде, изображенном на рис. 7.

Рис. 7. Граф G₁, изоморфный графу G, изображенному на рис. 1

Во-вторых, можно произвольно располагать вершины на плоскости. Например, вершины графа G можно расположить так, как показано на рис.8.

Если рассматривать три графа, изображенные на рис. 1, 7 и 8, как графы, описывающие ход спортивного турнира, то они будут содержать в точности одну и ту же информацию относительно того, какие именно команды уже играли друг с другом; в некотором смысле это один и тот же граф. Мы будем говорить, что два графа – обозначим их G₁ и G₂ – изоморфны, если они отвечают одному и тому же списку проведенных игр. Иными словами, если графы G₁ и G₂ изоморфны, то они имеют одно и то же число вершин и для любых двух вершин графа G₁ , скажем В₁ и С₁, соединенных ребром, соответствующие им вершины В₂ и С₂ графа G₂ тоже соединены ребром, и обратно.

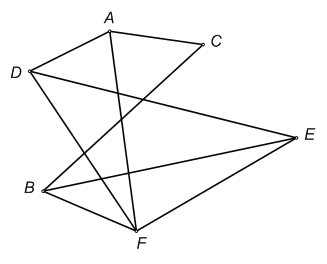
Рис. 8. Граф G₂, изоморфный графу G, изображенному на рис. 1 и графу G₁, изображенному на рис. 7

Согласно этому определению, три графа на рис. 1, 7 и 8 изоморфны (т. е. имеют одно и то же строение), хотя они и выглядят по-разному. (Термин «изоморфный» часто используется в математике; он состоит из греческих слов ιζωσ (isos) – равный, одинаковый и μορφε (morphē) – вид, форма).

Нередко приходится решать вопрос о том, являются ли два данных графа изоморфными. Иногда сразу ясно, что это не так. Например, графы, изображенные на рис. 9, не могут быть изоморфными, потому что они имеют неодинаковое число вершин.

Рис. 9. Пример неизоморфных графов

Не могут быть изоморфными и графы рис. 10, так как у них неодинаковое число ребер.

Рис. 10. Пример неизоморфных графов

Однако для того, чтобы показать, что не изоморфны графы, изображенные на рис. 11, требуется уже несколько более тонкое рассуждение.

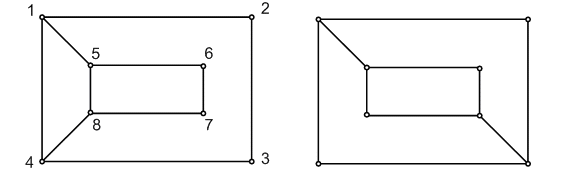
Рис. 11. Менее очевидный пример неизоморфных графов

Так, можно заметить, что на первом графе имеется последовательность из восьми смежных ребер (т. е. ребер, попарно имеющих общую вершину):

(1,2), (2,3), (3,4), (4,8), (8,7), (7,6), (6,5), (5,1),

возвращающаяся к исходной вершине, в то время как на втором графе такой последовательности нет. Значит, как бы ни были обозначены вершины второго графа, невозможно для каждой пары соединенных ребром вершин одного графа указать во втором соответствующую пару вершин, тоже соединенных ребром. (Докажите это!)

Если сразу не видно, как доказать, что два графа не изоморфны, то вопрос об их изоморфности может оказаться довольно трудным.

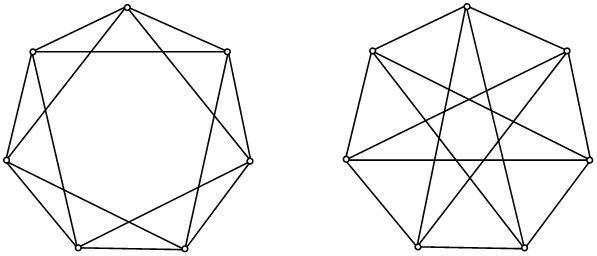
Рис. 12. Пример неочевидного изоморфизма графов

В качестве примера рассмотрим два графа, изображенных на рис. 12; эти графы на самом деле изоморфны.

Упражнения

1. Покажите, что графы, изображенные на рис. 1, 2, 6, не изоморфны между собой.

2. Укажите еще одну причину, в силу которой два графа рис. 11 не могут быть изоморфными.

3. Обозначьте вершины двух графов рис. 12 так, чтобы изоморфность этих графов стала очевидной.