10.3. Задачи обработки результатов моделирования

Наиболее ча­сто при обработке результатов компьютерного эксперимента возникают такие задачи, как сравнение средних значений и дисперсий переменных, полученных в результате моделирования, проверка однородности рас­пределений, определение эмпирического зако­на распределения случайной величины, и т. п. Подобные задачи являются типовыми задачами по проверке статистических гипотез.

Наиболее общей из названных выше является задача определения эмпирического закона распределения слу­чайной величины. Для ее пра­вильного решения требуется большое количество реализаций N. По результатам компьютерного эксперимента находятся значения выборочного закона распределения F_э(у) или функции плотности w_э(у) и выдвигается гипотеза Н_о, которая означает, что полученное эмпиричес­кое распределение согласуется с каким-либо теоретическим рас­пределением. Затем эта гипотеза Н_о проверяется с помощью статистичес­ких критериев согласия, причем необходимую в этом случае статистическую обработку ре­зультатов стараются вести непосредственно в процессе компьютерного моделирования систе­мы.

Далее выбирается некоторая случайная величина U, характеризующая степень расхождения теоретического и эмпирического распределения, связанную с недо­статочностью статистических данных и другими случайными причинами. Величина U служит для принятия или опровержения нулевой гипотезы Н_о. Закон распределения этой случайной величины зависит от закона распределения случайной величины η и числа реализаций N при статистическом моделировании системы. Если вероятность расхождения теоретического и эмпирического распределений Р{U_T≥U_Э} велика в понятиях применяемого критерия согласия, то проверяемая гипотеза о виде распределения Н₀ не опровергается. Выбор вида теоретического распределения F(у) или w(у) проводит­ся по графикам (гистограммам) F_э(у) или w_э(у), выведенным на печать или на экран дисплея.

Рассмотрим особенности использования при обработке резуль­татов компьютерного моделирования системы наиболее распространенных критериев согласия.

10.3.1. Критерий согласия Колмогорова

Критерий согласия Колмогорова основан на выборе в качестве меры расхожден­ия U величины D=max[F_э(у)–F(у)].

Из теоремы Колмогорова следует, что δ=D при N→∞ имеет функцию распределения

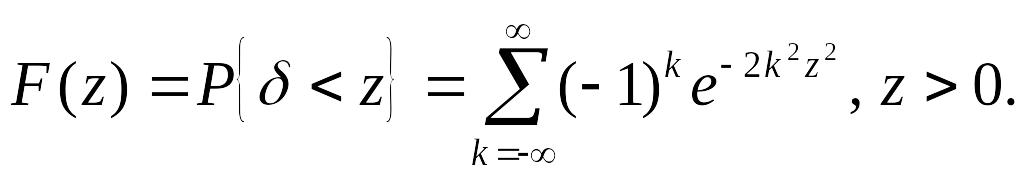
Если вычисленное на основе экспериментальных данных значение δ меньше, чем табличное значение при выбранном уровне значимости γ, то гипотезу Н_о принимают, в противном случае расхождение между F_э(у) и F(у) считается неслучайным и гипо­теза Н_о отвергается.

Критерий Колмогорова для обработки результатов моделирования целесообраз­но применять в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования этого критерия связан с необходимостью фиксации в памяти компьютера для определения D всех статистических частот с целью их упорядочения в порядке возрастания.

10.3.2. Критерий согласия Пирсона

Критерий согласия Пирсона основан на определении в качестве меры расхожден­ия U величины:

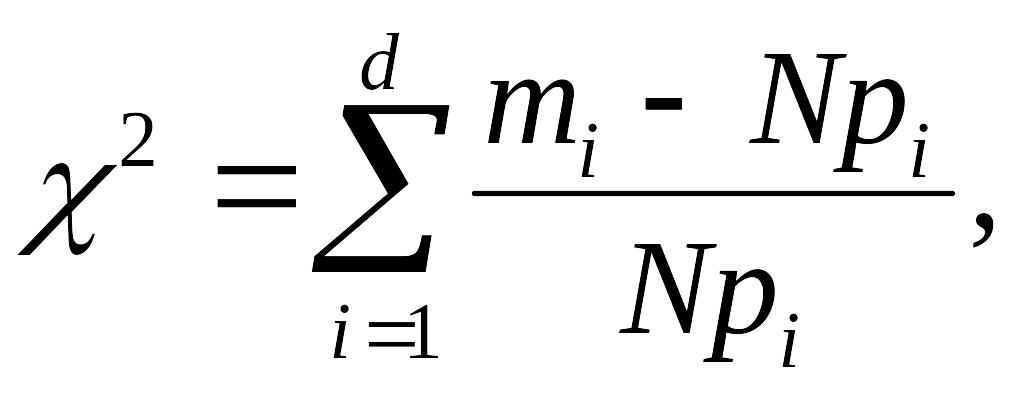
где m_i – количество значений случайной величины η, попавших в i-й подынтервал; p_i – вероятность попадания случайной величины η в i-й подынтервал, вычисленная из теоретического распределения; d – количество подынтервалов, на которые раз­бивается интервал измерения в компьютерном эксперименте.

При N→∞ закон распределения величины U, являющейся мерой расхождения, зависит только от числа подынтервалов и приближается к закону распределения χ² (хи-квадрат) с (d–r–1) степенями свободы, где r – число параметров теоретиче­ского закона распределения.

Из теоремы Пирсона следует, что, какова бы ни была функция распределения F(у) случайной величины η, при N→∞ распределение величины χ² имеет вид:

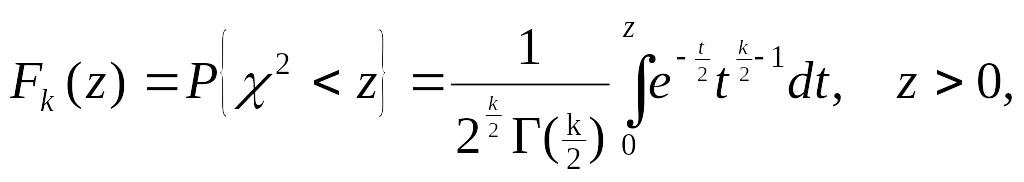
где Г(k/2) – гамма-функция; z – значение случайной величины χ²; k=d–r–1 – число степеней свободы. Функции распределения F_k(z) табулированы.

По вычисленному значению U=χ² и числу степеней свободы k с помощью таблиц находится вероятность Р{ }. Если эта вероятность превышает некото­рый уровень значимости γ, то считается, что гипотеза Н₀ о виде распределения не опровергается результатами компьютерного эксперимента.