Метод Гаусса

Суть метода Гаусса заключается в приведении матрицы коэффициентов к диагональному виду. Это выполняется в 2 этапа: прямой ход – обнуляются элементы под главой диагональю

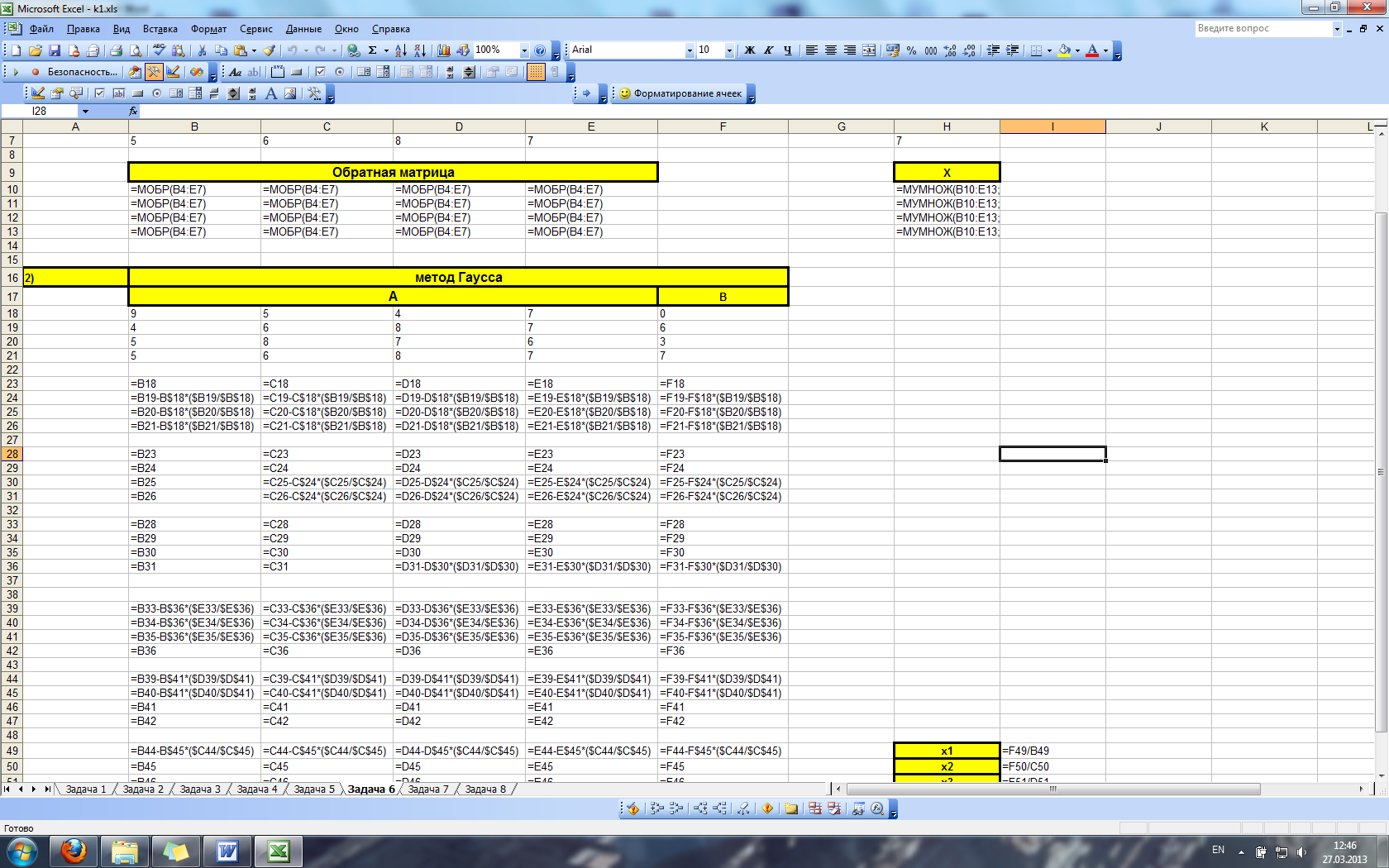
Рис. 20

И обратный ход – обнуляются элементы над главной диагональю

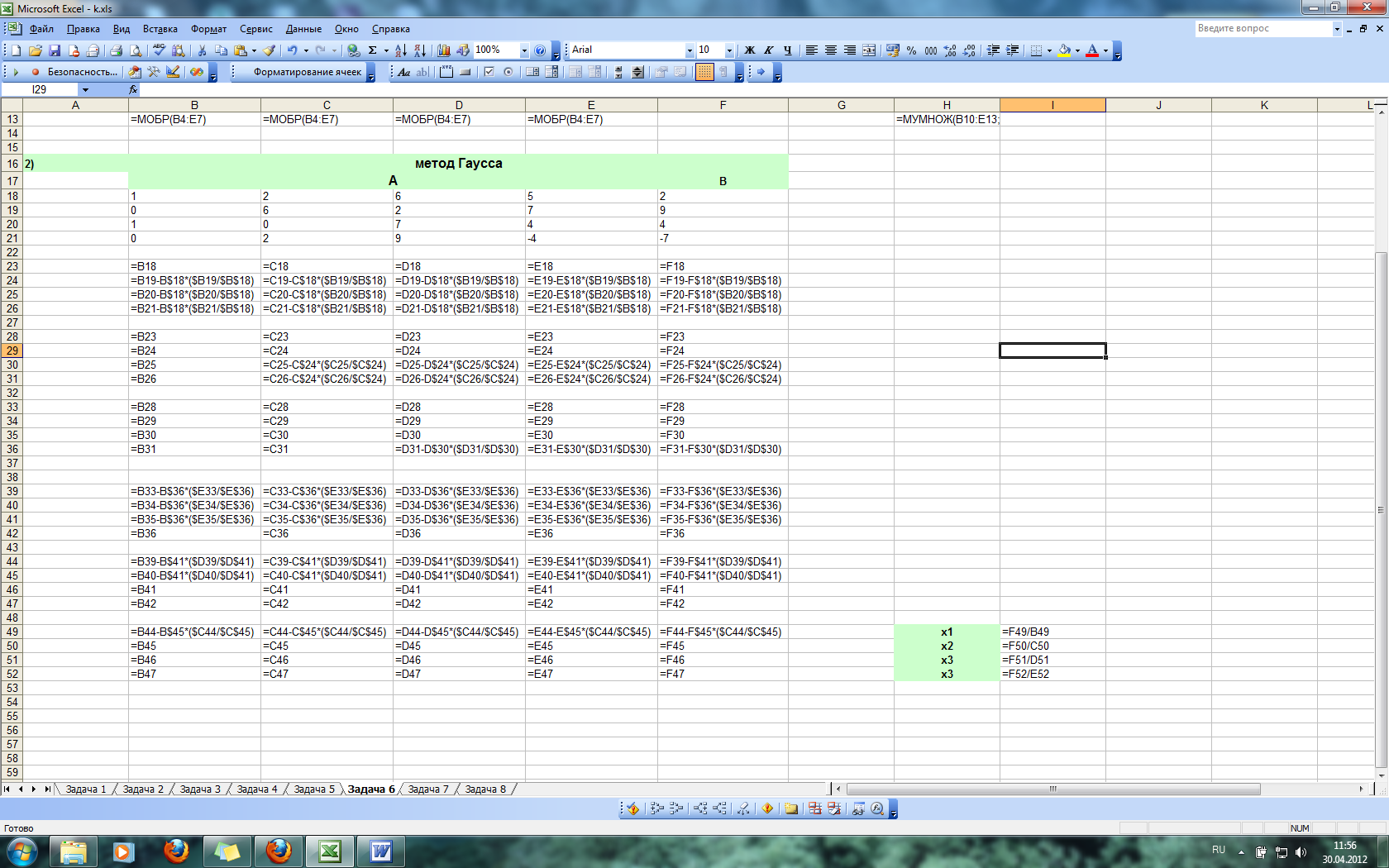
Рис. 21

В результате имеем диагональную матрицу:

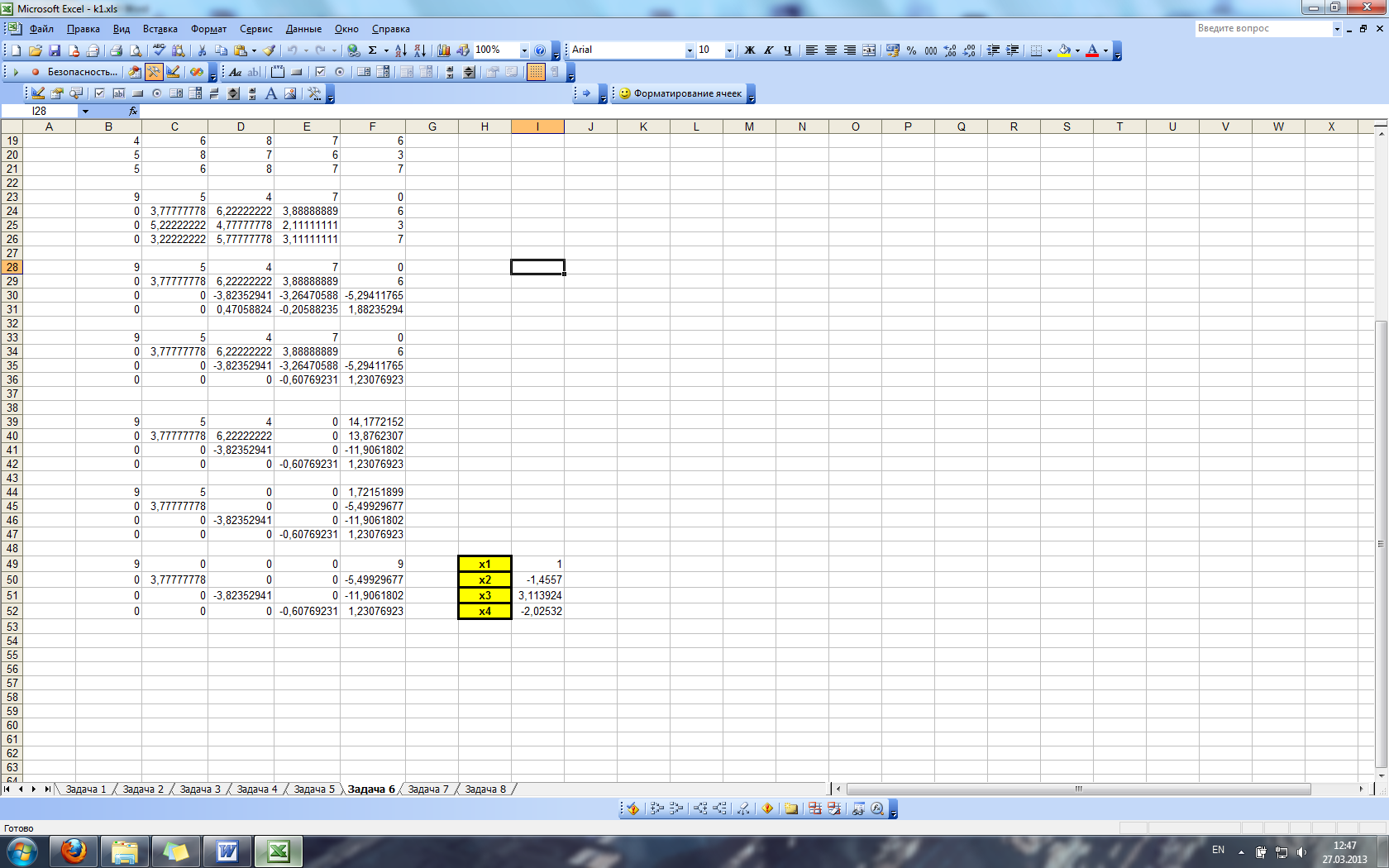
Рис. 22

После чего решения находятся по формулам:

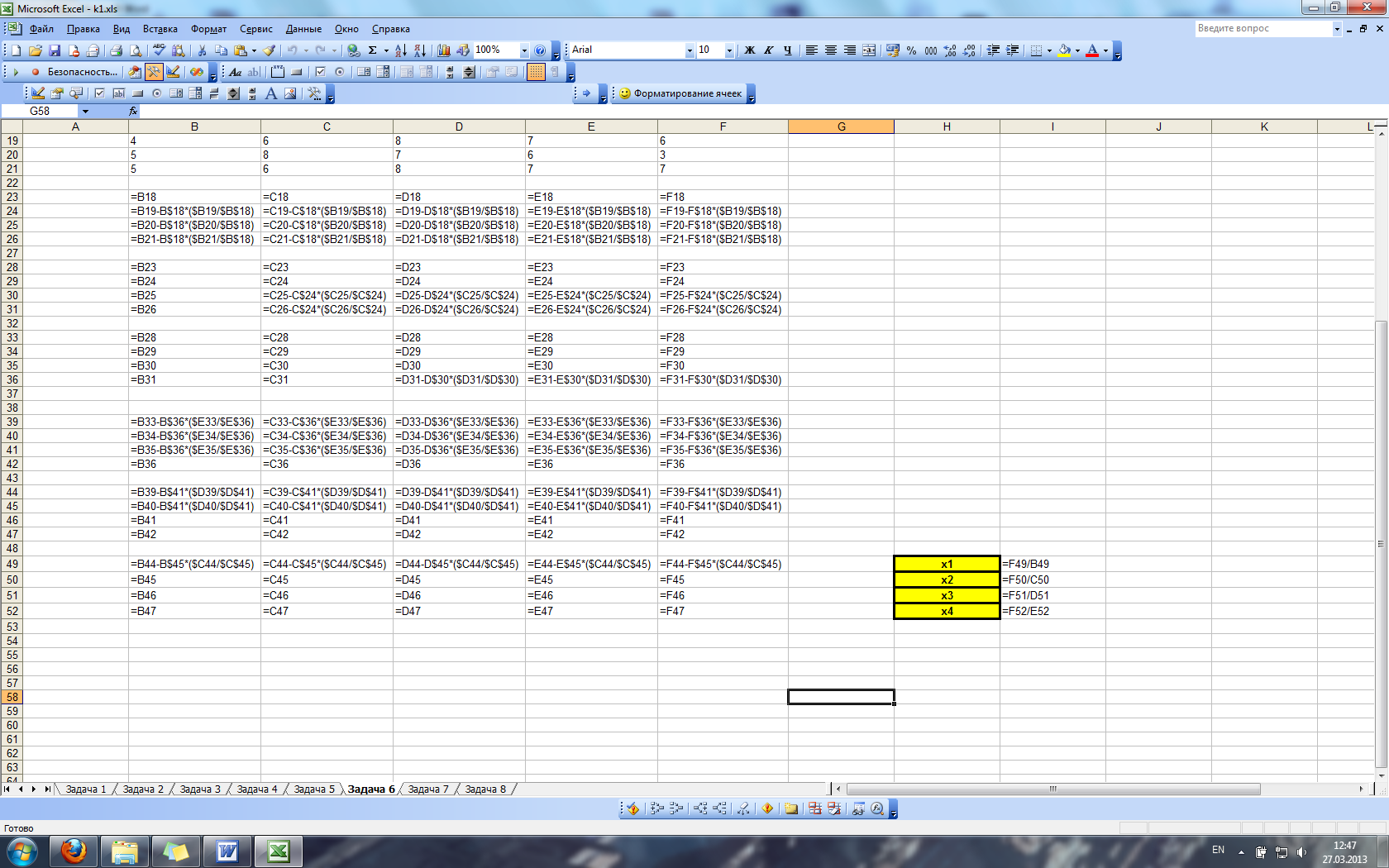
Рис. 23

В результате имеем:

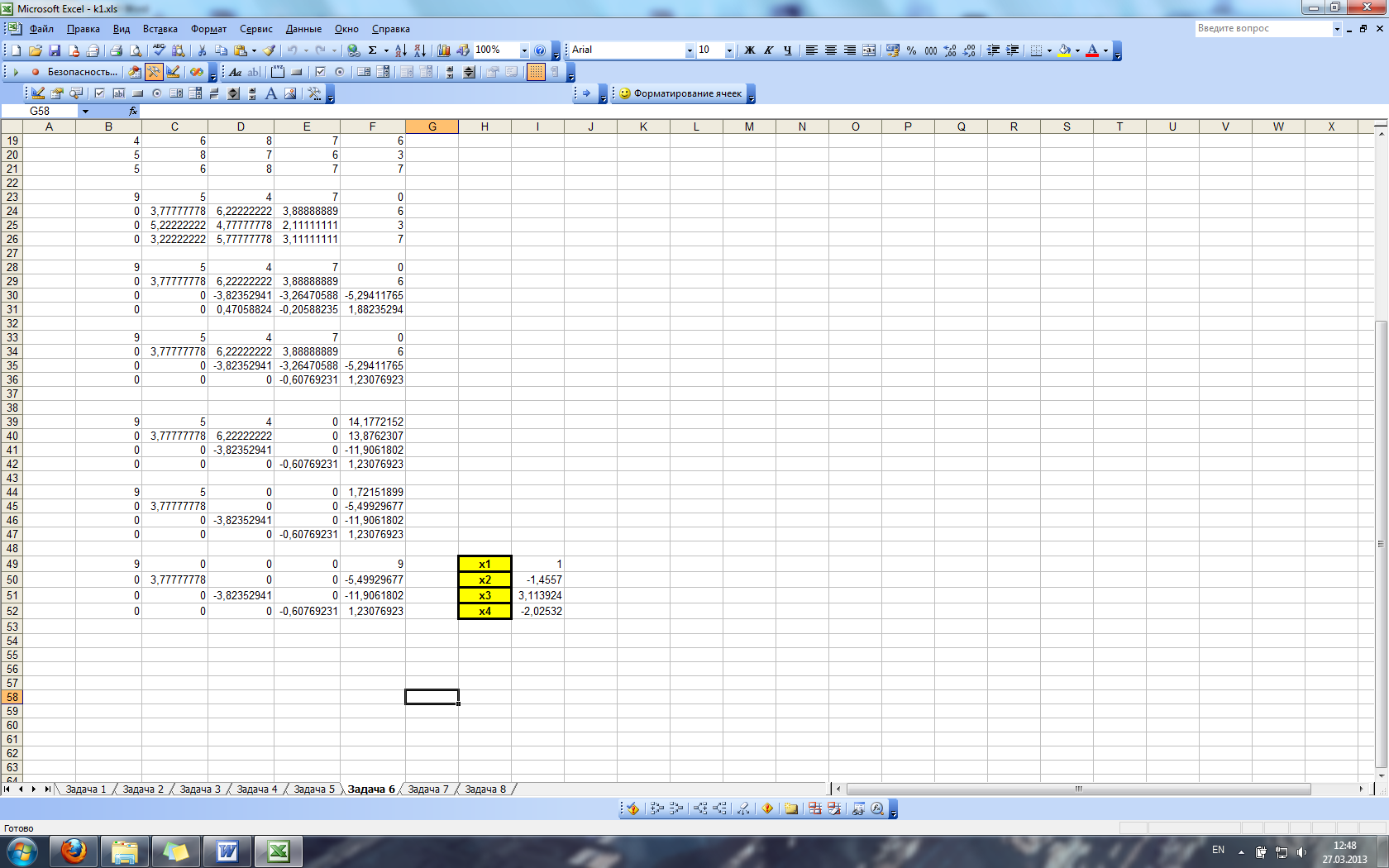
Рис. 24

Задание 7

По адресу http://kit.znu.edu.ua/iLec/3sem/kurs/labrab2.exe найти файл labrab2.exe и скопировать его в свою папку. Запустив программу, создать текстовый файл исходных данных. Преобразовать полученные данные в табличный формат MS Excel и выполнить следующие задания:

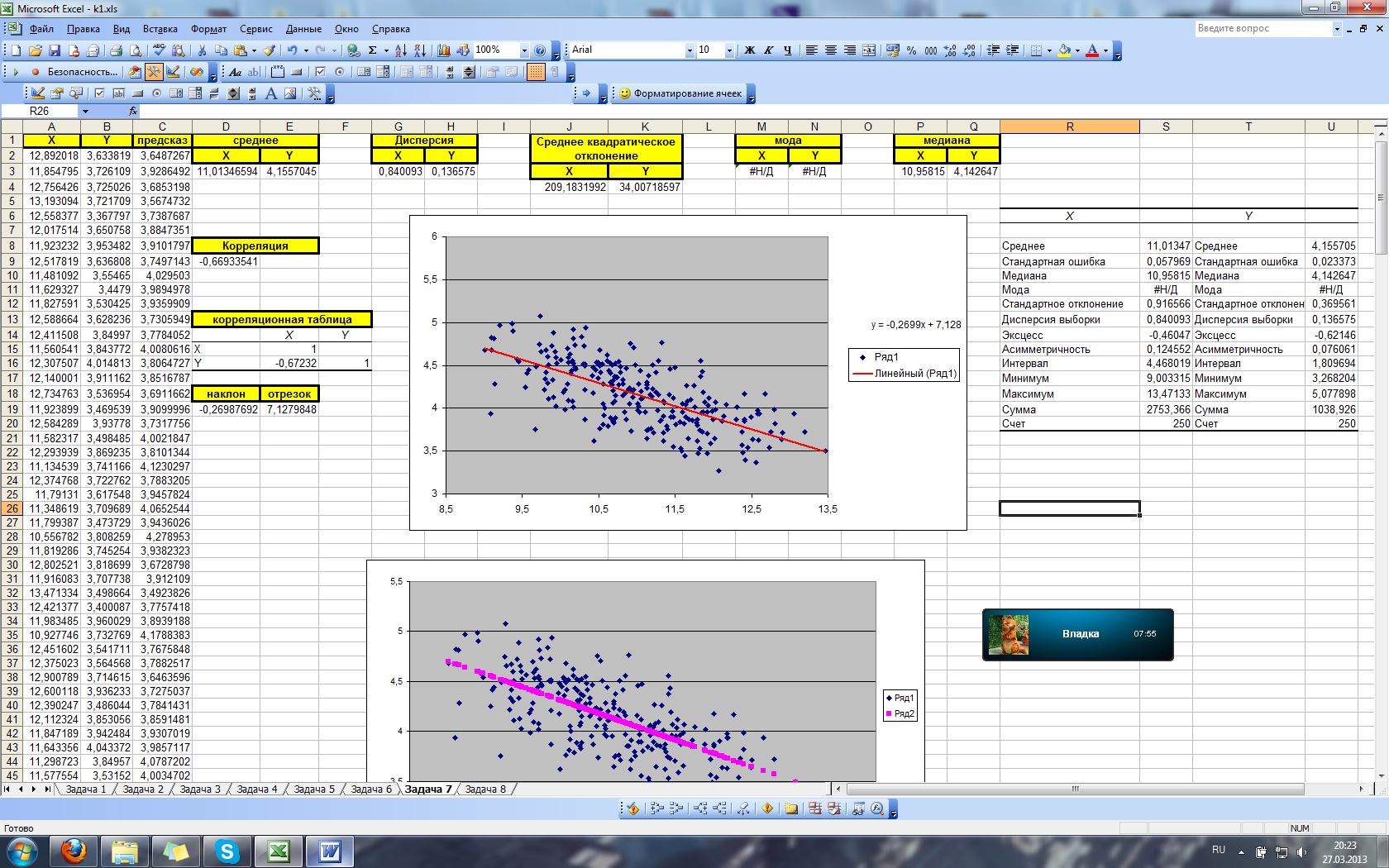
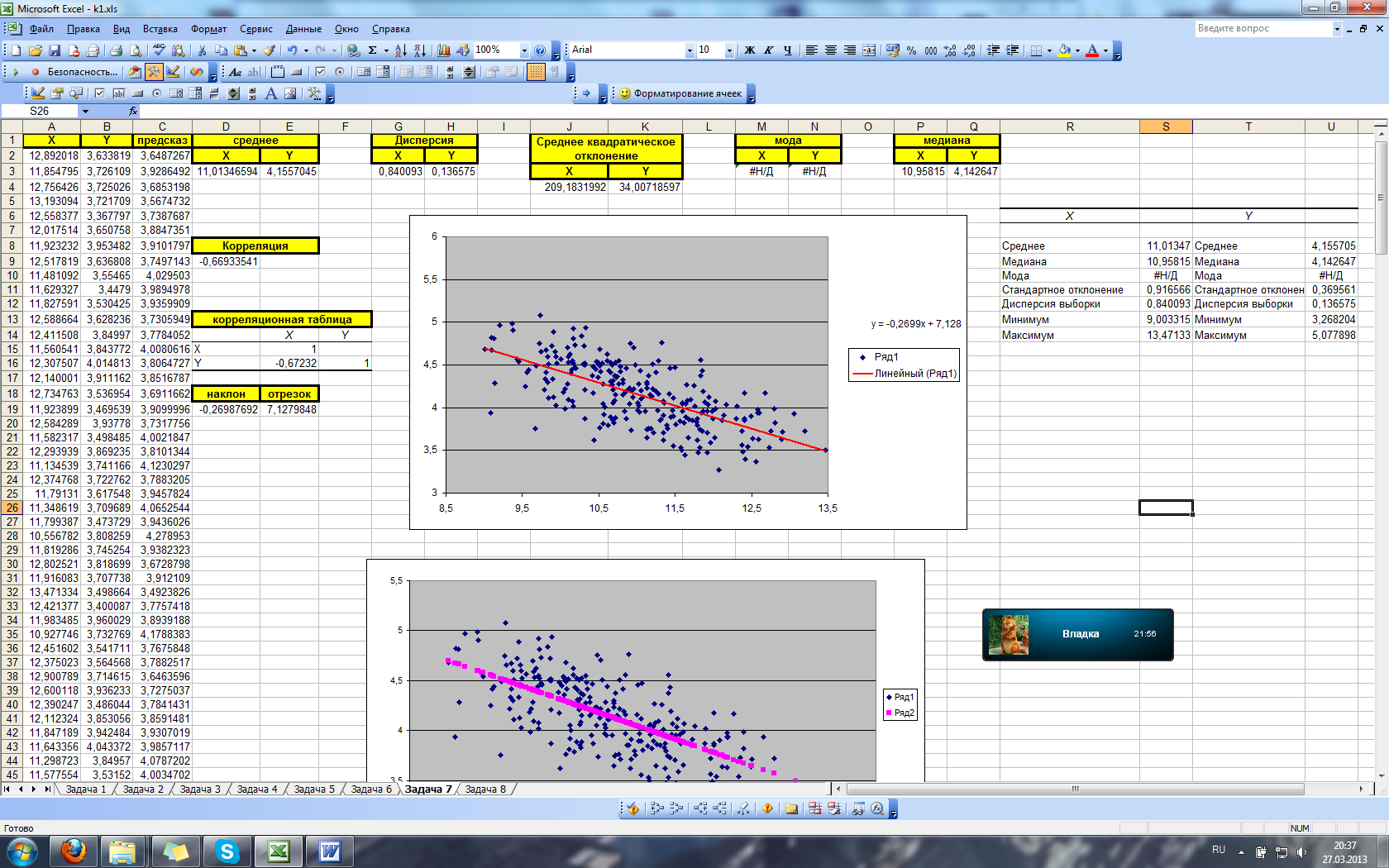
a)        Используя встроенные статистические функции MS Excel и Анализ данных, вычислить по предлагаемым данным среднее арифметическое, дисперсию, среднее квадратическое отклонение, моду, медиану для каждой случайной величины.

b)       Используя встроенную статистическую функцию MS Excel и инструмент Корреляция Анализа данных вычислить коэффициент корреляции двух случайных величин.

c)        Используя функции НАКЛОН и ОТРЕЗОК (получение уравнения линейной регрессии), а также функцию ПРЕДСКАЗ (получение теоретических значений по линии регрессии) исследовать зависимость второй случайной величины (y) от первой (x); построить корреляционное поле и график теоретической линии регрессии (на основании данных, полученных по функции ПРЕДСКАЗ). Для проверки параметров теоретической линии регрессии построить линию тренда (на другом графике) с указанием уравнения регрессии.

При помощи файла labrab2.exe получим набор исходных данных и импортируем его в MS Excel, разместив в ячейках A2:B251

Найдем основные статистические параметры, используя инструмент Анализ данных/Описательная статистика:

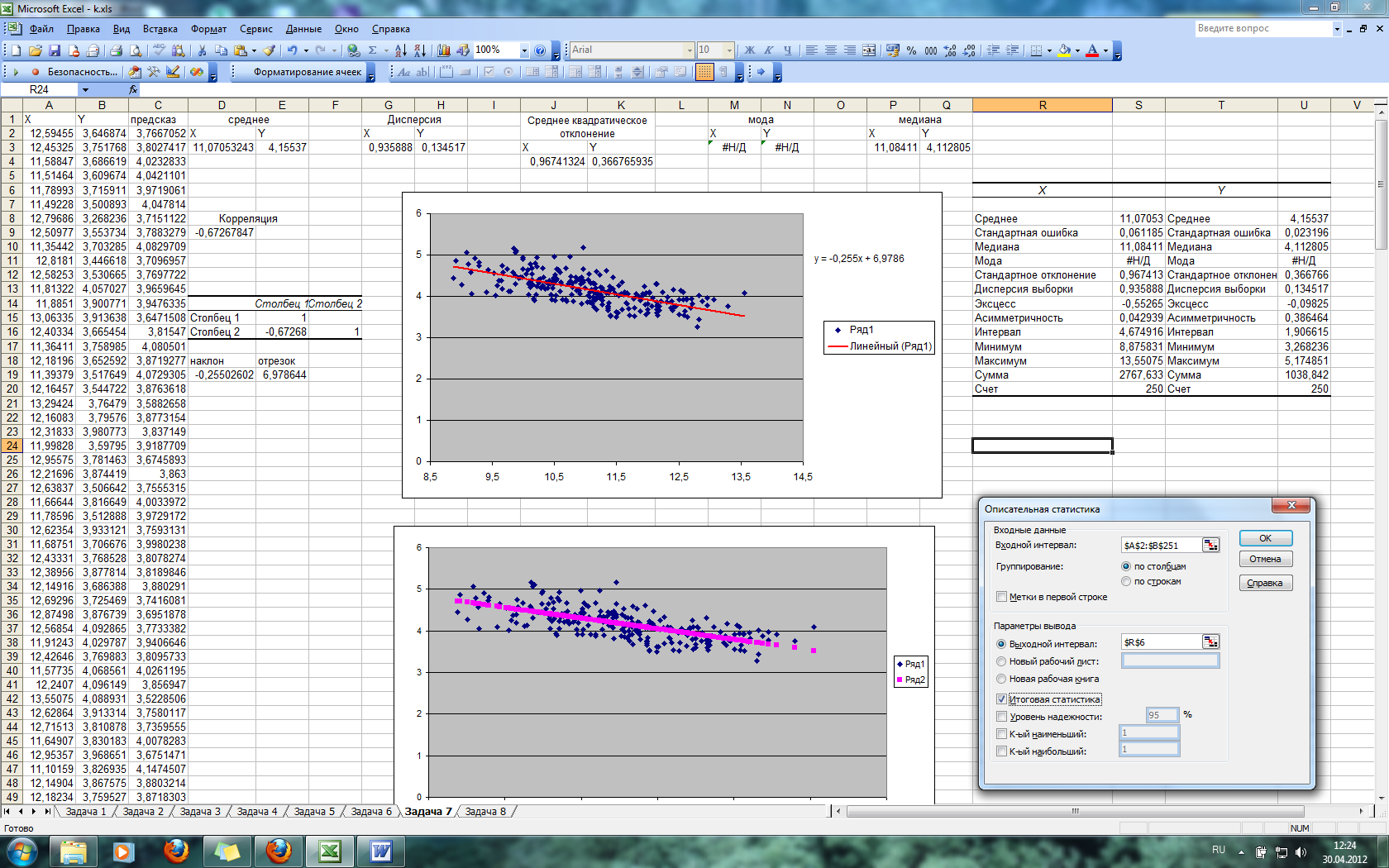
Рис. 25

В результате выполнения этого инструмента будет получена таблица (слева), которую необходимо преобразовать, удалив ненужные данные (справа):

Рис. 26

Рис. 27

Используя инструмент Анализ данных/Корреляция найдем корреляцию между следующими параметрами: X и Y. В диалоговом окне Корреляция задаются следующие параметры:

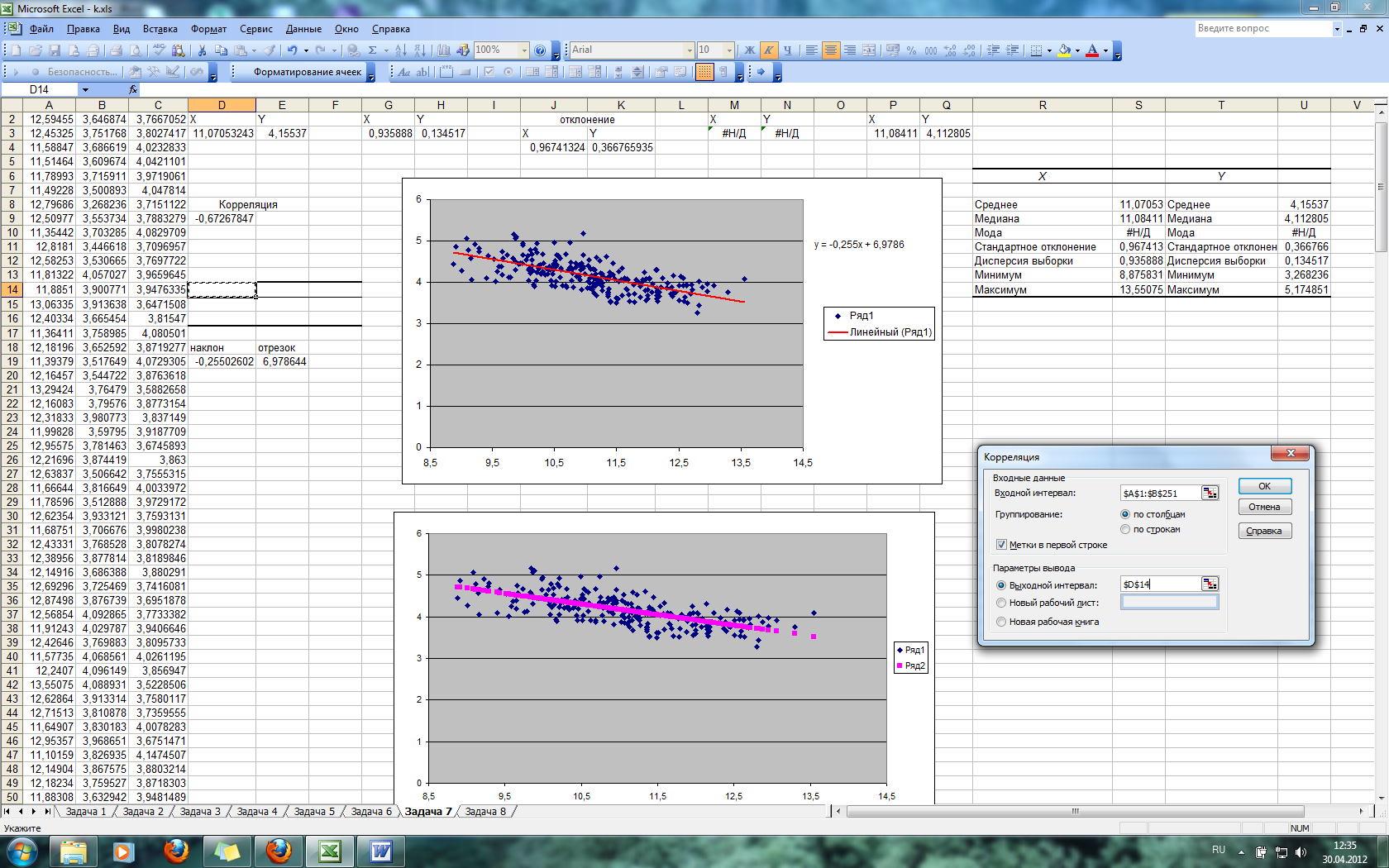
Рис. 28

В результате выполнения этого инструмента получается корреляционная таблица:

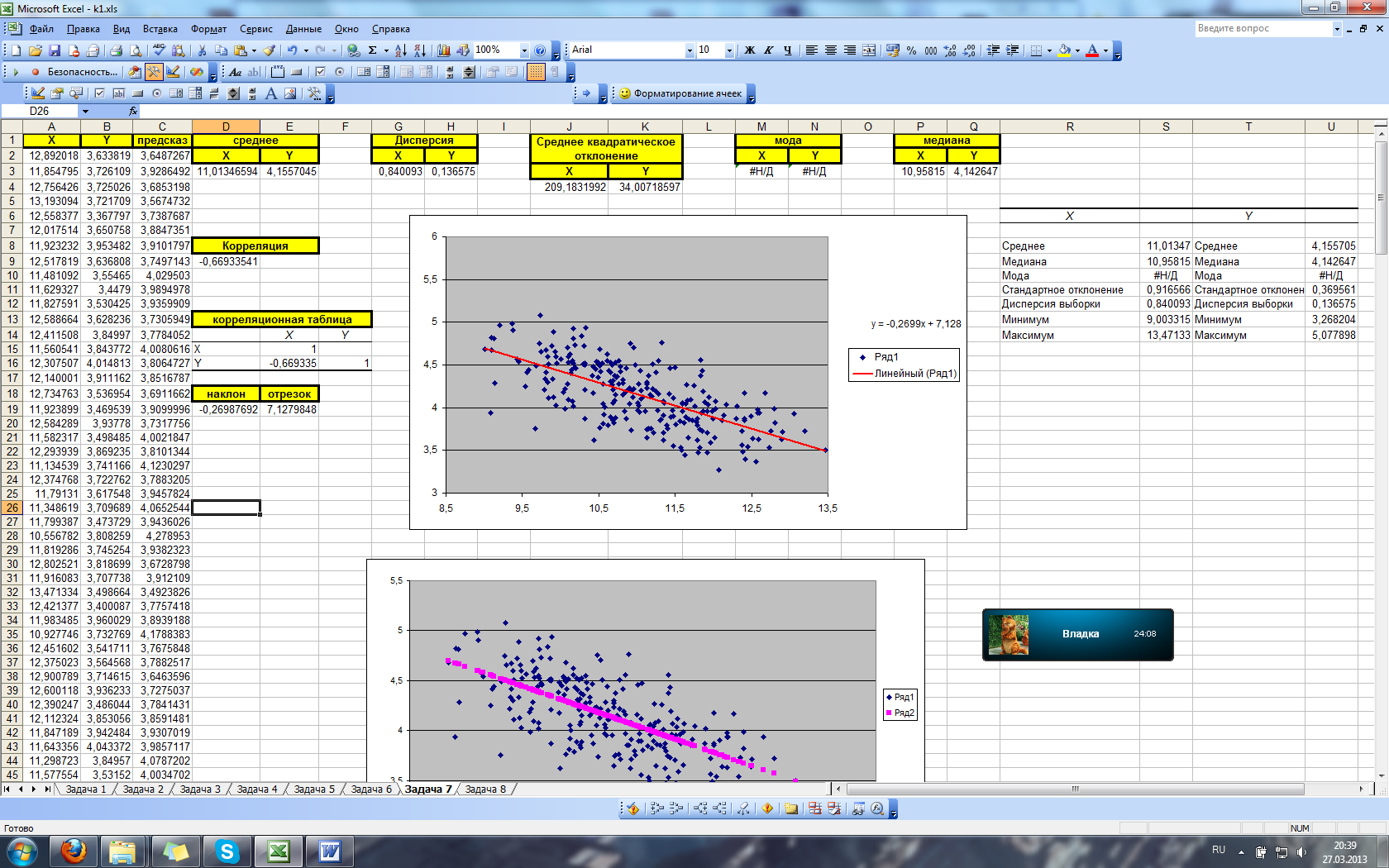
Рис. 29

Для нахождения среднего арифметического, дисперсии, среднего квадратического отклонения, моды и медианы для каждой случайной величины воспользуемся стандартными функциями:

Рис. 30

В результате получим:

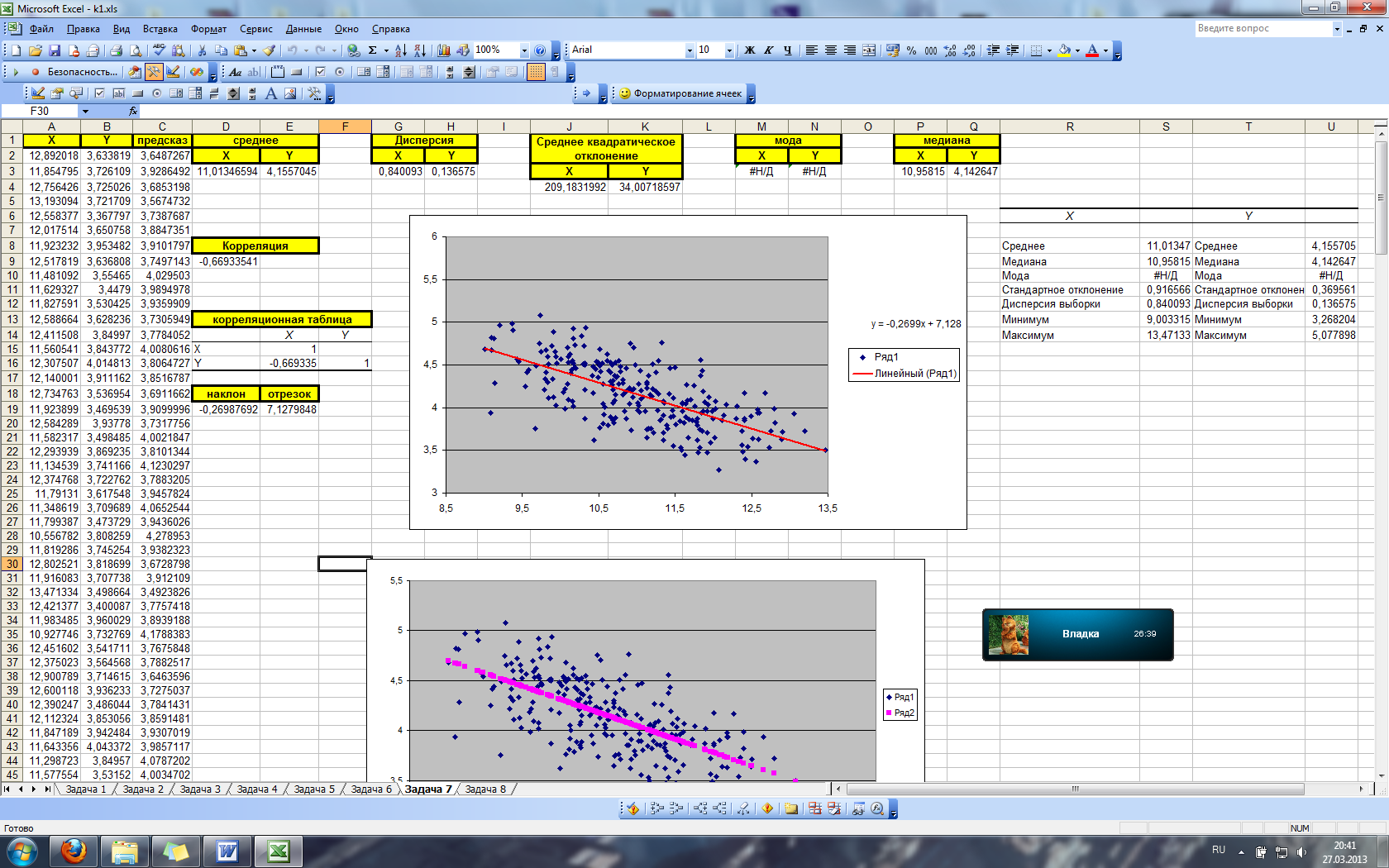
Рис. 31

Для определения теоретических значений у, используется функция ПРЕДСКАЗ. Для вычисления теоретического Y в ячейке С2 используется формула:

=ПРЕДСКАЗ(A2;$B$2:$B$251;$A$2:$A$251)

Построим корреляционное поле и график теоретической линии регрессии (на основании данных, полученных по функции ПРЕДСКАЗ)

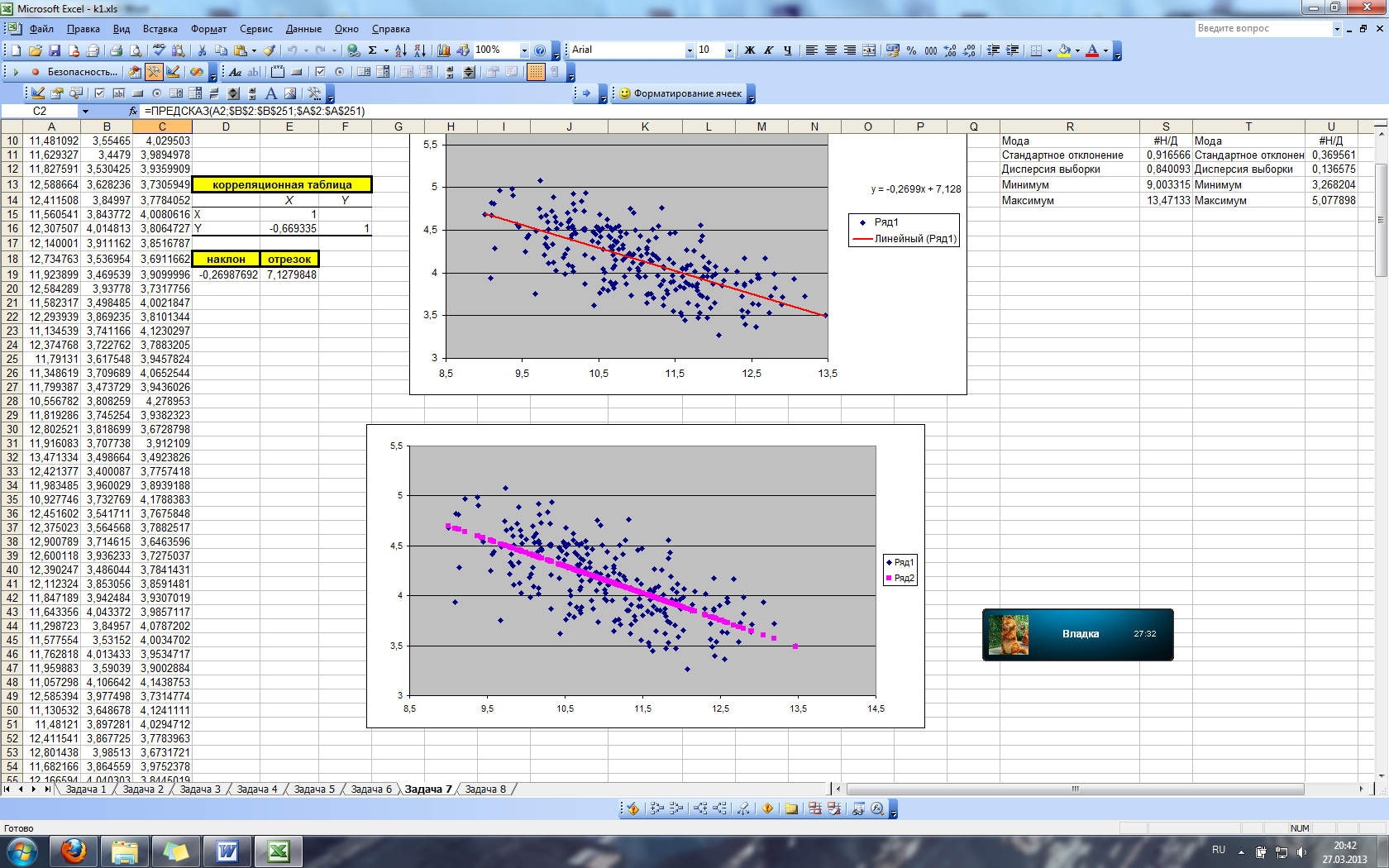
Рис. 32

Для построения уравнения теоретической линии регрессии на основании столбцов X и Y находим коэффициенты, используя соответствующие функции:

=НАКЛОН(B2:B251;A2:A251)

=ОТРЕЗОК(B2:B251;A2:A251)

В результате получим:

Рис. 33

Для проверки параметров теоретической линии регрессии построим линию тренда с указанием уравнения регрессии. Для построения графика выбирается тип графика – Точечная диаграмма. После чего добавляем на него линию тренда.

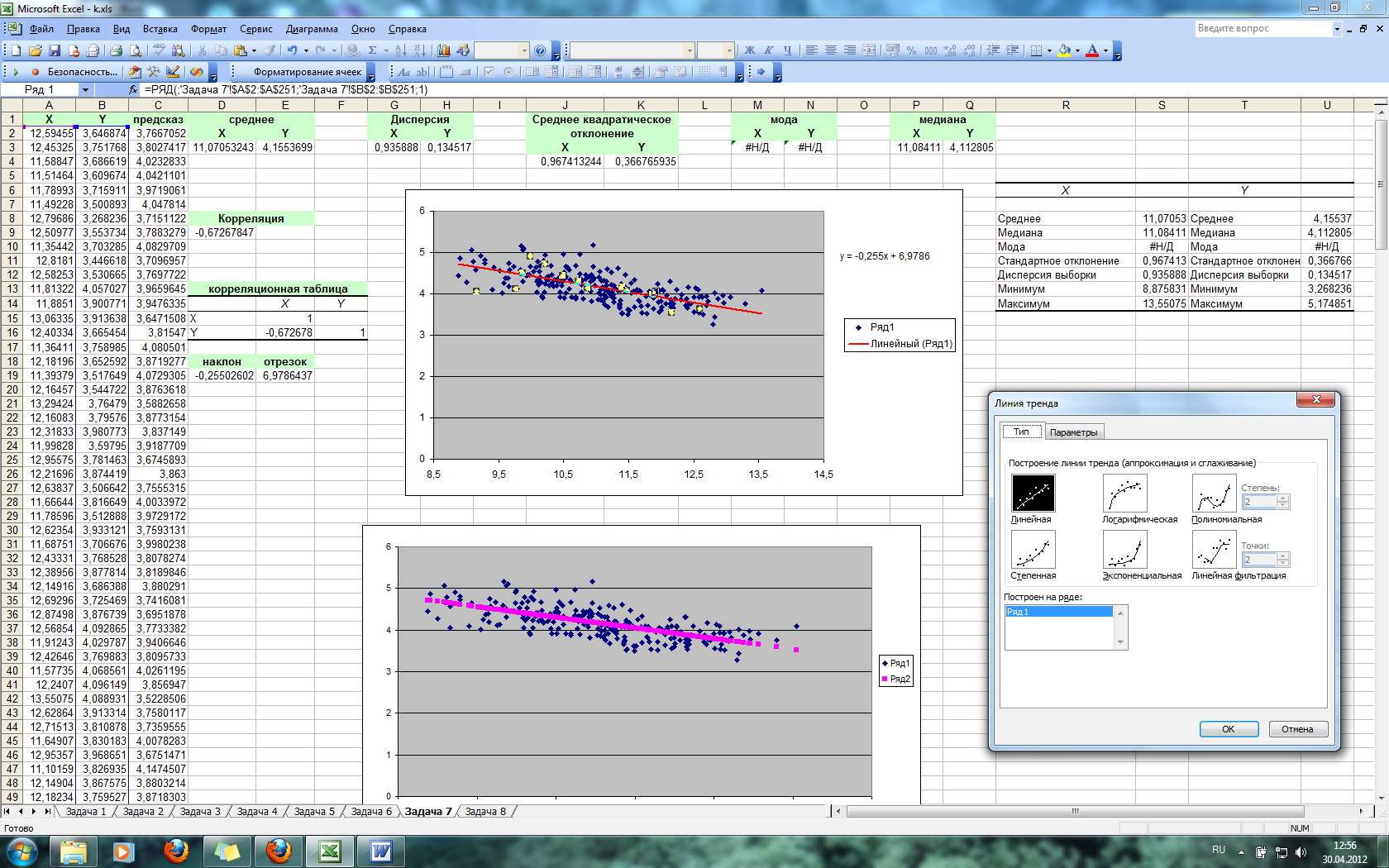
Рис. 34

После чего имеем:

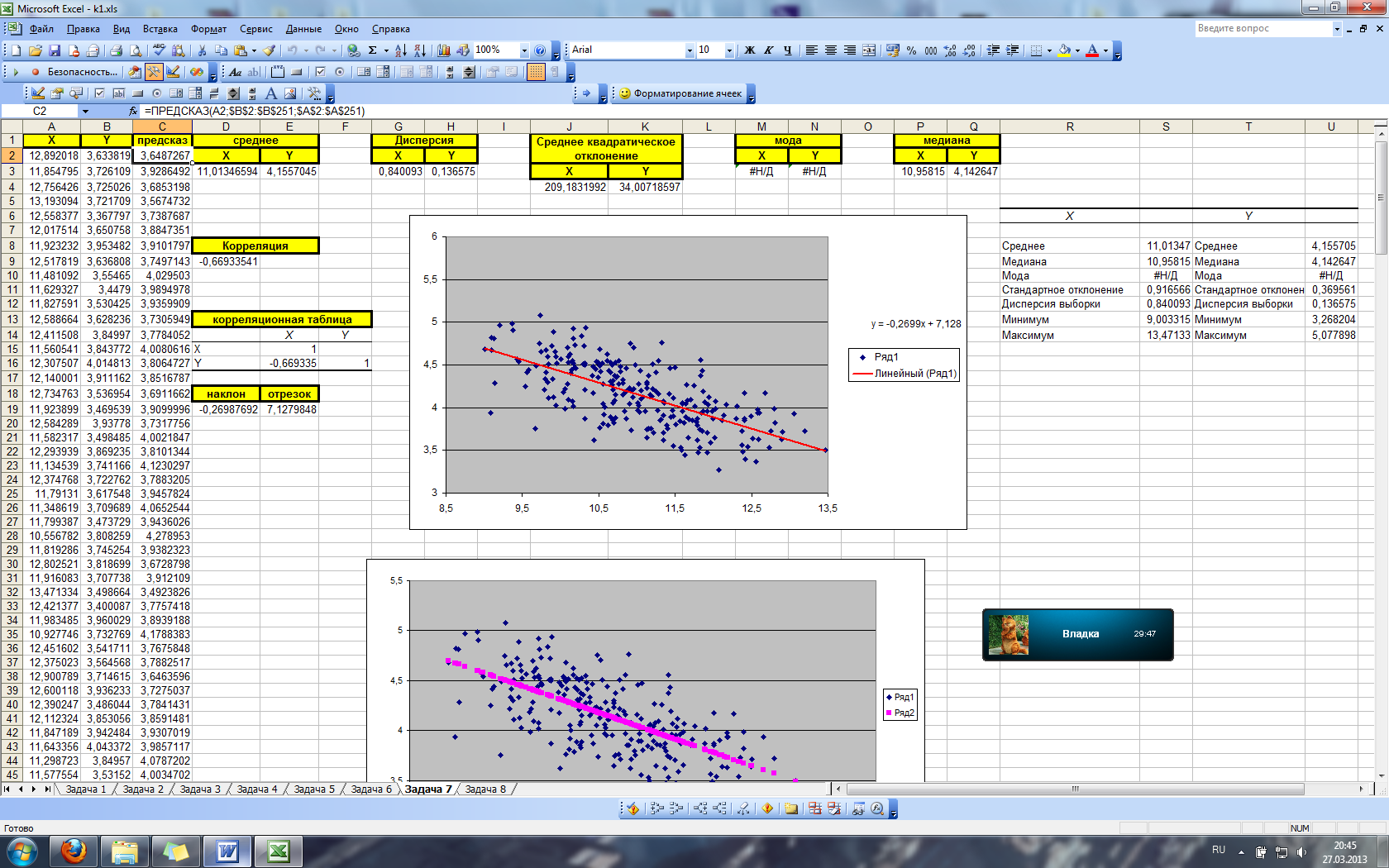
Рис. 35