5 Примеры решения задач домашней контрольной работы Задача № 1

Алгоритм решения:

1. Выделяют объект равновесия, т.е. тело или точку, равновесие которых в данной задаче следует рассмотреть.

2. К выделенному объекту равновесия прикладывают заданные силы.

3. Выделенную точку или тело освобождают от связей и вместо них прикладывают реакции связей (аксиома 6).

4. Выбирают координатные оси и составляют уравнения равновесия, используя условия равновесия системы сходящихся сил на плоскости ΣFix =0 ; ΣFiу = 0.

5. Решают составленные уравнения и определяют реакции стержней.

6. Найденные неизвестные величины проверяют с помощью уравнений равновесия, не использованных при их определении, либо решают задачу графически.

Пример.

y

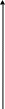
Согласно рисунку .1.1, Определить реакции стержней АВ и ВС, под действием приложенных сил F₁=100 кН и F₂=50 кН. Массой стержней пренебречь.

Y₁

R_AB

А

30^°

15°

30°

В

x

R_BC

45°

45°

С

F₂

F₁

F₂

45°

В

45°

F₁

Рисунок 1.1 Рисунок 1.2

1. Выделяем в качестве объекта равновесия узел В.

2. Прикладываем к нему заданные силы F₁, F₂.

3. Освобождаем узел В от связей, т.е. отбрасываем стержни АВ и ВС и прикладываем их реакции R_АВ, R_ВС. Эти реакции направлены от узла В, как показано на рисунке 1.2. Это соответствует предположению, что оба стержня АВ и ВС растянуты.

4. Выбираем координатные оси таким образом, чтобы одна из них прошла по реакции. Находим углы наклона сил к осям х и у. Составляем уравнения равновесия для плоской системы сходящихся сил:

ΣFix = 0; -R_ВС –R_AB cos 60⁰ +F₂ cos 45⁰ = 0;

ΣFiу = 0; R_АВ cos 30⁰ - F₁ – F₂ cos 45⁰ = 0

5. Решаем полученную систему уравнений:

R_AВ = (F₁ + F₂ cos 45⁰)/ cos 30⁰ = (100 + 50·0,707)/0,866 = 156,3 кН

Знак плюс перед численным значением реакции R_АВ показывает, что стержень АВ, как и предполагалось, растянут силой R_АВ = 156,3 кН

Из первого уравнения определяем:

R_ВС = –R_AB cos 60⁰ +F₂ cos 45⁰= -156,3·0,5 + 50·0,707 = - 42,8 кН

Знак минус перед численным значением реакции R_ВС показывает, что стержень ВС в действительности не растянут, а сжат силой R_ВС = 42,8 кН.

6. Решение задачи следует обязательно проверять. Лучшим способом проверки может быть либо решение с использованием иных координатных осей, либо решение другим методом, например графическим.

Выбираем ось координат у₁, как показано на рисунке 1.2 и составляем уравнение на эту ось.

ΣFi_Y1 = 0; - F₂ + R_АВ cos 15⁰ + R_ВС cos 45⁰– F₁ cos 45⁰ = 0;

- 50 + 156,3·0,966 +(-42,8) ·0,707 - 100·0,707 = 0;

0 = 0

Задача № 2

Алгоритм решения задачи:

1. Изобразить балку вместе с нагрузками;

2. Выбрать расположение координатных осей, совместив ось Х с балкой, а ось У

направив перпендикулярно оси Х;

3. Произвести необходимые преобразования заданных активных сил: равномерно распределенную нагрузку по закону прямоугольника – ее равнодействующей, приложенной в середине участка распределения нагрузки;

4. Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат.

5. Составить уравнения равновесия статики и определить неизвестные реакции опор;

6. Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.

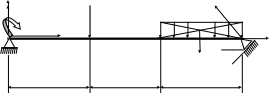
Пример. Определить реакции опор балки согласно рисунку 2.1.

1. Изображаем балку с действующими на нее нагрузками рисунок 2.2.

2. Изображаем оси координат.

3. Равнодействующая 4q равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника, переносится по линии своего действия в середину участка КВ, в точку С.

4. Отбрасываем опорные закрепления и заменяем их действия реакциями R_Ay, R_Ax, R_B.

F=50кН

m=20кН·м q=10кН/м

А В

60⁰

3м 3м 4м

Рисунок 2.1

у R_В

R_Ау F q

m R_Ах

х

А К С В

4q 60⁰

3м 3м 4м

Рисунок 2.2

5. Составляем уравнения равновесия для плоской системы произвольно расположенных сил и определяем неизвестные реакции опор.

ΣMa=0; m + F·3 + 4·q·8 - R_B·10·cos60⁰=0;

ΣMв=0; m + R_Ay·10-F·7-4q·2=0;

ΣF_ix=0; R_Ax - R_B·cos30⁰=0;

Решаем полученную систему уравнений:

R_B=(m+ F·3 + 4·q·8) / (10·cos60⁰)=(20+50·3+4·10·8) / (10·0,5)= 98 кН;

R_Ay=(-m + F·7 + 4q·2)/10=(-20+ 50·7 +4·10·2)/10= 41 кН;

R_Ax=R_B·cos30⁰= 98 ·0,866 = 84,9 кН.

6. Выполняем проверку найденных величин:

Проверка

ΣF_iу=0: R_Ay-F-4·q+R_B·cos60⁰=0;

41 – 50 -4·10 +98·0,5=0;

0=0