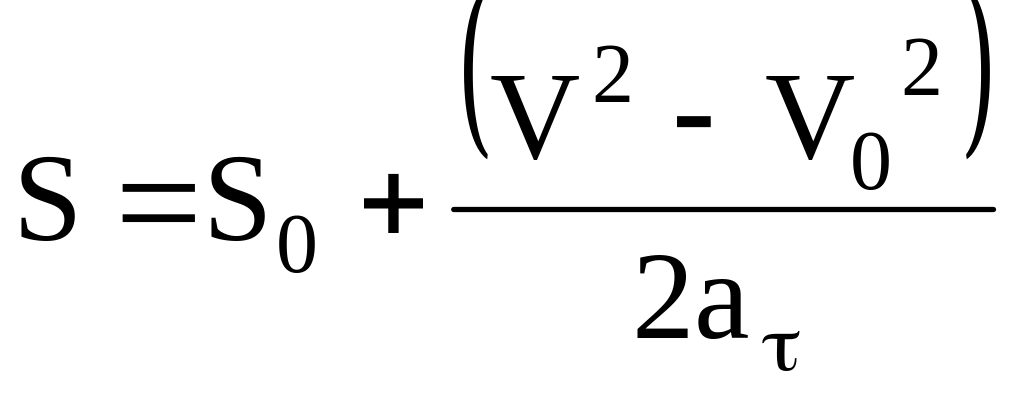Содержание учебного материала

Кинематика как наука о механическом движении. Покой и движение. Траектория, расстояние, путь, время, скорость и ускорение.

Способы задания движения точки. Уравнение движения. Скорость и ускорение точки при естественном способе задания. Виды движения точки в зависимости от ускорения. Равномерное и равнопеременное движение точки, их уравнения.

Поступательное движение твердого тела. Вращательное движение твердого тела вокруг неподвижной оси. Угловое перемещение. Уравнение вращательного движения, угловая скорость и угловое ускорение тела. Частота вращения. Скорость и ускорения точек вращающегося тела.

Методические рекомендации

Кинематика имеет весьма важное значение не только для изучения последнего раздела теоретической механики, динамики, но и для исследования геометрических свойств движения частей различного рода механизмов.

Всякое механическое движение материального тела можно наблюдать и изучать лишь по отношению к каким-либо другим телам. Обратите внимание, что тело, по отношению к которому с помощью системы координат определяется положение других тел в разные моменты времени, называется системой отсчёта.

В процессе своего движения точка последовательно занимает различные положения относительно принятой системы отсчёта, причём эти положения непрерывно следуют одно за другим. Геометрическое место положений движущейся точки в рассматриваемой системе отсчёта называется траекторией этой точки. Запомните, траектория может быть прямолинейной и криволинейной. Форма траектории зависит от выбора системы отсчёта.

Далее внимательно рассмотрите понятия «расстояние» и «путь».

Далее перейдите к изучению наиболее важных понятий кинематики «скорость» и «ускорение».

Скорость – векторная величина, характеризующая в каждый момент времени быстроту и направление движения точки. Выражается скорость в м/с, км/ч, м/мин. Рассмотрите, как направлен вектор скорости при прямолинейном и криволинейном движении точки, а также, обратите внимание, что модуль средней скорости равен частному от деления пройденного пути на время, в течение которого этот путь пройден.

Ускорение – векторная физическая величина, характеризующая быстроту изменения направления и числового значения скорости. За единицу ускорения принимают обычно 1м/с². Рассмотрите способ определения направления вектора среднего ускорения точки. Модуль среднего ускорения равен частному от деления изменения значения скорости на время, в течение которого произошло это изменение. Обратите внимание, что при равномерном движении (скорость является постоянной величиной) по криволинейной траектории точка тоже имеет ускорение, так как и в этом случае изменяется направление вектора скорости.

Прежде чем начать изучение и классификацию движения точки, необходимо ознакомиться со способами задания её положения по отношению к выбранной системе отчёта в любой момент времени, т.е. со способами задания её движения. Из применяемых в механике способов задания движения точки рассмотрите два: естественный и координатный.

Естественный способ заключается в том, что движение точки задаётся её траекторией и уравнением движения. Уравнение движения записывается в общем случае так: S = f (t)

Обратите внимание, что значение скорости точки, движение которой задано естественным способом, в любой момент времени равно первой производной от расстояния по времени: V =d S/ d t.

Так как скорость величина векторная, то заметьте, что при прямолинейном движении точки вектор скорости совпадает с траекторией её движения, при криволинейном движении точки вектор скорости в каждый момент времени направлен по касательной к траектории в сторону движения точки.

При прямолинейном движении точки вектор скорости совпадает с траекторией её движения и поэтому вектор изменения скорости также совпадает с траекторией.

Таким образом, истинное ускорение в прямолинейном движении равно первой производной от скорости в данный момент по времени или второй производной от расстояния по времени: а = d V / d t = f ' (t).

При движении точки по криволинейной траектории вектор скорости меняет своё направление, следовательно, и вектор ускорения тоже. Для удобства расчетов в данном случае ускорение раскладывают на взаимно перпендикулярные составляющие по касательной и нормали к траектории движения. Проекция полного ускорения на нормаль к траектории называется нормальным ускорением а_n; проекция полного ускорения на касательную к траектории называется касательным ускорением а _τ.

Модуль касательного ускорения равен производной от скорости в данный момент по времени или второй производной от расстояния по времени и характеризует быстроту изменения скорости: а _τ = d V / d t = f ' (t).

Если векторы V и a_τ направлены в одну и ту же сторону, то движение точки называется ускоренным. Если же векторы V и a_τ направлены в противоположные стороны, то движение точки называется замедленным.

Модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент и обратно пропорционален радиусу кривизны траектории в данной точке и характеризует быстроту изменения направления скорости: а_n = V²/ρ.

Модуль полного ускорения: .

Направление вектора полного ускорения [угол α = (a, V)] находим с помощью тригонометрических функций по одной из следующих формул: ; ; .

Координатный способ задания движения точки применяется в том случае, если траектория точки заранее не известна, тогда положение точки в пространстве определяется тремя координатами: абсциссой х, ординатой у и аппликатой z по отношению к прямоугольной системе координат Охуz.

В частном случае, если точка движется в плоскости, закон движения точки выражается двумя уравнениями: х=f₁(t); y=f₂(t).

Обратите внимание, если движение точки задано в координатной форме, то уравнения х=f1(t); y=f2(t) описывают движения не самой точки, а ее проекций вдоль соответствующих осей. Первое из уравнений определяет закон изменения абсциссы х движущейся точки, т.е. описывает движения по оси абсцисс точки Ах – проекции точки А на ось х. Второе уравнение определяет закон изменения ординаты у точки А, т.е. описывает движение по оси ординат ее проекции Ау на эту ось.

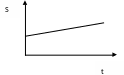
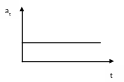
Учитывая, что в общем случае ускорение точки раскладывается на два слагаемых: касательное ускорение a_τ , которое характеризует быстроту изменения модуля скорости и служит характеристикой неравномерности движения по любой траектории и нормальное ускорение а_n, которое характеризует быстроту изменения направления скорости и является характеристикой криволинейности движения рассмотрите частные случаи движения точки, когда одно или оба слагаемых равны нулю либо сохраняют отличное от нуля постоянное значение. Описанные ниже движения точки как при решении задач, так и просто ради большей наглядности целесообразно изображать в виде графиков расстояний, скоростей и касательных ускорений, построенных в осях (S, t), (V, t) (a_τ, t) с соблюдением соответствующих масштабов.

1. Прямолинейное
2. Равномерное
3. Равномерное прямолинейное
t 4. Равнопеременное	Вспомогательные формулы	t

V

Рассмотрите последовательно простейшие виды движения тела: поступательное и вращательное.

Поступательным называется движение твёрдого тела, при котором, любой выбранный в теле отрезок прямой перемещается, оставаясь параллельным своему первоначальному положению. Обратите внимание, что при поступательном движении все его точки перемещаются одинаково - траектории всех точек тела одинаковы, скорости и ускорения всех точек тела в каждый данный момент времени равны между собой. Отсюда следует, что поступательное движение твёрдого тела полностью характеризуется движением любой его точки. Обычно поступательное движение тела задаётся движением его центра тяжести.

Вращательным называется движение твёрдого тела, при котором, все его точки перемещаются по окружностям с центрами, расположенными на перпендикулярной этим окружностям неподвижной прямой (оси вращения). Заметьте, что при вращении наблюдается угловое перемещение, определяемое углом поворота φ, выраженным в радианах. Чтобы определять положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота φ и временем t, то есть знать закон вращательного движения тела, заданный уравнением: φ = f (t).

Последовательно рассмотрите понятия: угловая скорость, угловое ускорение. Угловая скорость ω характеризует быстроту изменения угла поворота во времени и выражается в рад/с. Угловое ускорение ε характеризует быстроту изменения угловой скорости во времени и выражается в рад/с².

Подробно рассмотрите формулы для определения угловой скорости и углового ускорения (средних и в данный момент времени).

В технике часто скорость вращения выражают в оборотах в минуту и называют частотой вращения. Запомните связь между угловой скоростью и частотой вращения тела.

Далее изучите частные случаи вращательного движения тела (равномерное и равнопеременное). Равномерным называется вращение тела вокруг неподвижной оси с постоянной угловой скоростью. Равнопеременным называется вращение тела с постоянным угловым ускорением.

Точки вращающегося тела движутся неодинаково, но, зная закон вращательного движения тела, можно определить скорость и ускорение точки в любой момент времени. Для этой цели рассмотрите установленную зависимость между угловыми величинами, характеризующими вращательное движение тела, и линейными величинами.

Сравните формулы кинематики точки или поступательно движущегося тела с формулами вращательного движения тела с помощью таблицы.

Кинематическая мера движения	Характер движения	Вид движения
		поступательное	Вращательное
Перемещение	Неравномерное	S = f (t )	φ = f (t )
	Равномерное	S = V t	φ = ω t
	Равнопеременное	S = V0 t +а t + а t2/2	φ = ω 0 t + ε t + ε t2/2
Скорость	Неравномерное	V =d S/ d t	ω =d φ /d t
	Равномерное	V =const	ω =const
	Равнопеременное	V = V0 + а t	ω = ω 0 + ε t
Ускорение касательное	Неравномерное	а = d V / d t	ε = d ω / d t
	Равномерное	а = 0	ε = 0
	Равнопеременное	а = const	ε = const
Ускорение нормальное		аn = V2/ρ	аn = ω2 ρ

[ 1 ] §§ 58-67; [ 2 ] §§ 1.25 -1.28, §§ 1.31-1.34.