Содержание учебного материала

Чистый сдвиг. Закон Гука при сдвиге. Модуль сдвига. Крутящий момент. Эпюры крутящих моментов. Кручение прямого бруса круглого поперечного сечения. Напряжения и деформации при кручении бруса круглого сечения.

Полярные моменты сопротивления сечения для круга и кольца. Методика расчета валов на прочность и жесткость при кручении.

Методические рекомендации

Изучение темы необходимо начать с основных определений. Кручение – такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный силовой фактор – крутящий момент Т.

Деформация кручения возникает при нагружении бруса парами сил, плоскости действия которых перпендикулярны его продольной оси. Моменты этих пар называют скручивающими моментами (Те).

Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, то есть брус находится в равновесии.

Крутящий момент, возникающий в произвольном поперечном сечении бруса, определяется с помощью метода сечений. Он численно равен алгебраической сумме скручивающих моментов, приложенных к оставленной части.

Знак крутящего момента не имеет физического смысла, но для определённости при построении эпюр условимся о следующем правиле знаков: считаем крутящий момент положительным, если для наблюдателя, смотрящего на проведённое сечение, он представляется направленным по часовой стрелке и отрицательным, если против часовой стрелки.

График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов.

Далее нужно рассмотреть деформацию сдвига, как она происходит, в чём заключается и чем характеризуется.

Чистый сдвиг – это частный случай плоского напряжённого состояния, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четырёх его гранях были только равные между собой касательные напряжения, а две грани свободны от напряжений.

Закон парности касательных напряжений:

Касательные напряжения на двух взаимно перпендикулярных площадках направлены оба одновременно либо к ребру, либо от ребра пересечения площадок, на которых они возникают.

Деформация сдвига состоит в том, что под действием внешних сил первоначальная форма выделенного элемента искажается, то есть, например, горизонтальные площадки сдвигаются относительно друг друга на расстояние Δdz, называемое абсолютным сдвигом, и угол 90⁰ между смежными площадками изменяется на величину γ – угол сдвига (угловая деформация), который является мерой деформации сдвига и выражается в радианах.

Закон Гука при сдвиге:

В пределах упругих деформаций между углом сдвига и касательными напряжениями существует прямо пропорциональная зависимость.

где G – модуль сдвига (модуль упругости 2-го рода) – упругая постоянная материала, характеризующая его жёсткость при сдвиге.

В среднем для стали G=8·10⁴МПа=8·10¹⁰Па.

Для одного и того же материала между модулем упругости Е, модулем сдвига G и коэффициентом Пуассона существует зависимость

После этого можно перейти к изучению напряжений и перемещений при кручении бруса круглого поперечного сечения.

Теория бруса круглого поперечного сечения или кольцевого поперечного сечения основана на следующих допущениях:

1. Поперечные сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации (гипотеза Бернулли).

2. Радиусы поперечных сечений при деформации бруса не искривляются.

3. Материал бруса при деформации следует закону Гука.

Рассмотрим брус, жёстко защемлённый одним концом и нагруженный на свободном конце скручивающим моментом. При деформации бруса его поперечные сечения повернутся на некоторые углы по отношению к своему первоначальному положению (по отношению к заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки.

φ – угол закручивания.

Угол поворота произвольного сечения равен углу закручивания части бруса, заключённой между этим сечением и заделкой.

Выразим крутящий момент через касательные напряжения, возникающие в поперечном сечении. В любой точке поперечного сечения касательное напряжение направлено перпендикулярно радиусу, проведённому в эту точку (так как при повороте поперечного сечения каждая его точка перемещается по дуге окружности).

Касательные напряжения в поперечном сечении меняются по длине радиуса по линейному закону.

При кручении происходит деформация сдвига в результате вращательного движения одного поперечного сечения относительно другого.

Формула для определения касательных напряжений:

где Iр – полярный момент инерции сечения;

ρ – радиус;

Т – крутящий момент.

В точках равноудалённых от центра сечения, напряжения одинаковы. Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения.

Введём обозначение

Wp – полярный момент сопротивления сечения. Является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении (м³; см³; мм³).

Полярные моменты сопротивления сечения

1. Круг

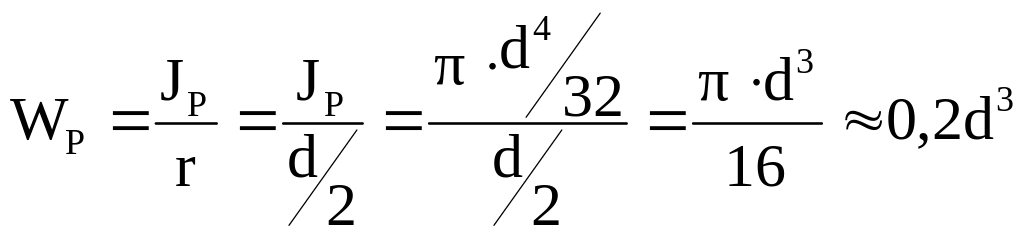
2. Кольцо

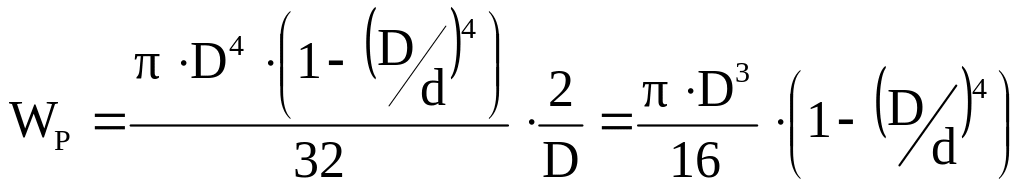
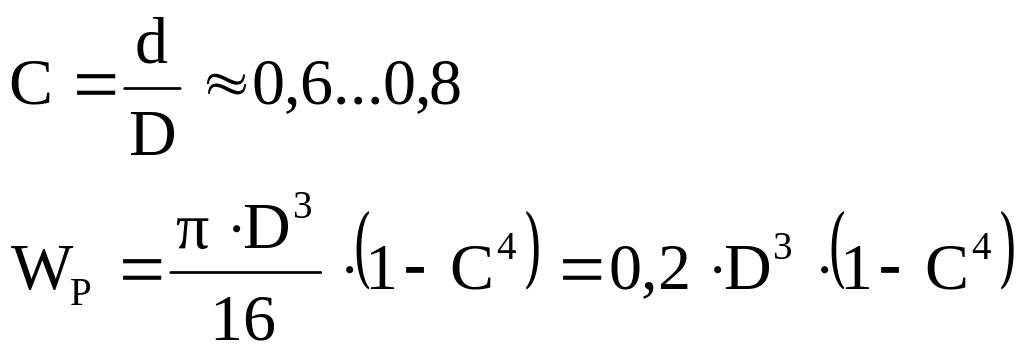
Угол закручивания

Деформация бруса при кручении характеризуется углом взаимного поворота двух сечений (углом закручивания). Полный угол закручивания бруса длиной l определяется по формуле

Произведение условно называют жёсткостью сечения круглого бруса при кручении.

Далее нужно ознакомиться с расчётами на прочность и жёсткость при кручении.

Расчёты на прочность при кручении

Условие прочности при кручении имеет вид

где - наибольшее касательное напряжение в опасном поперечном сечении бруса

Обратите внимание, что существует 3 вида расчётов на прочность: проверочный, проектный, определение допускаемого крутящего момента.

Расчёт на жёсткость

За меру жёсткости при кручении принимают относительный (погонный) угол закручивания (угол закручивания на единицу длины) φ.

Условие жёсткости при кручении имеет вид:

где =(0,25...1) град/м.

Допускаемый угол закручивания зависит от назначения вала.

Существует 3 вида расчётов на жёсткость: проверочный, проектный (подбор сечения), определение допускаемого крутящего момента.

Из двух значений диаметра вала, определённых из расчётов на прочность и жёсткость, в качестве окончательного должен быть принят больший.

[1] §§ 39-42; [2] §§ 2.14-2.18.