Итак, если линейная часть линейной асу является фильтром низких частот, т.Е. Выполняется неравенство:
/Wл(jkω0)/<</Wл(jω0)/, k = 2,3,…, (9)
то в ней возможны автоколебания, которые на выходе линейной части (и, следовательно, на выходе нелинейности) близки к гармоническим. В этом случае вместо исходной нелинейной структурной схемы (рисунок 1) можно рассматривать линейную, изображённую на рисунке 2.
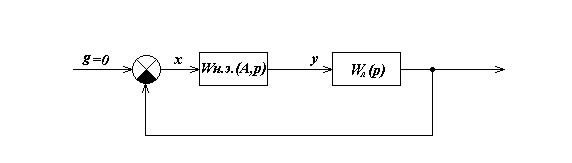
Рисунок 2 – Структурная схема АСУ
Последняя, однако, позволяет выявить специфические свойства линейной системы, так как коэффициенты q(A) и q’(A) передаточной функции Wн.э(A,р) гармонически линеаризованной нелинейности зависят от амплитуды А. При некоторых нелинейностях эти коэффициенты зависят также и от частоты ω0 автоколебаний.
Метод исследования нелинейных систем, основанный на гармонической линеаризации нелинейной части системы, называется методом гармонической линеаризации или методом гармонического баланса.
Так как автоколебания близки к гармоническим, то они полностью определяются двумя параметрами: амплитудой А и частотой ω0. Их значения могут быть найдены из условия, что незатухающие колебания возникают в линейной системе только в том случае, если она находится на границе устойчивости. Это условие, в частности, на основании критерия устойчивости Найквиста, может быть записано в виде:
.
(10)
Здесь Wн.э(A) есть комплексный коэффициент передачи гармонически линеаризованного нелинейного элемента, и он определяется из его передаточной функции подстановкой р = jω:
Wн.э(A,jω) = q(A) + jq’(A). (11)
Подставив это выражение для Wн.э(A), а также выражение Wл(jω) = Q(jω)/D(jω) для частотной передаточной функции линейной части, уравнение (10) можно переписать так:
D(jω) + Q(jω)·{q(A) + jq’(A)} = 0. (12)
Каждое из комплексных уравнений (10) и (12) равносильно системе двух действительных уравнений:
U(ω,A) = 0; V(ω,A) = 0, (13)
где U(ω,A) и V(ω,A) – действительные и мнимые части выражения левой части уравнения (12).
Если уравнение (10) или, что то же, система (13) не имеет вещественных положительных решений, то в рассматриваемой АСУ автоколебания невозможны. Если же указанные уравнения имеют вещественные положительные корни ω0 и А0, то это означает, что уравнения (12), описывающие свободные движения в АСУ, имеют решение:
.
(14)
Это решение определяет гармонические колебания, которые могут быть устойчивыми и неустойчивыми. Только устойчивые колебания являются автоколебаниями.
Параметры ω0 и А0 гармонических колебаний могут быть определены графически. При этом уравнение (10) удобнее переписать следующим образом:
Wл(jω) = -Wн.э-1(A), (15)
или
Wл-1(jω) = -Wн.э(A). (16)
В соответствии с равенством (15) на одной комплексной плоскости необходимо построить годограф Wл(jω), изменяя ω от 0 до ∞, и годограф -Wн.э-1(A), изменяя А от минимального возможного значения (определяемого видом нелинейности) до ∞ (рисунок 3). Если решение (13) существует, то эти годографы пересекаются. По годографу -Wн.э-1(A) в точке пересечения определяется амплитуда и по годографу Wл(jω) – частота ω0 .
Порядок полинома числителя передаточной функции Wл(р) линейной части обычно меньше порядка полинома её знаменателя. Поэтому удобнее пользоваться равенством (16) и строить годографы Wл-1(jω) и -Wн.э(A) (рисунок 4).
После определения параметров гармонических колебаний необходимо исследовать их устойчивость. При графическом определении параметров устойчивость проверяется следующим образом. На годографе -Wн.э-1(A) или -Wн.э(A) отмечается точка С, соответствующая амплитуде
А = А0 + ΔА,
где ΔА – достаточно малое положительное число.
Если при движении по годографу Wл(jω) (рисунок 3,а) или годографу Wл-1(jω) (рисунок 4,а) в сторону возрастания частоты точка С находится слева, то гармонические колебания устойчивы, справа (рисунок 3,б), (рисунок 4,б) – неустойчивы.
В случае, когда q’(A) = 0 (характеристика нелинейного элемента является однозначной), гармонические колебания, соответствующие параметрам А и ω0, устойчивы, если Wн.э(A) является убывающей функцией в окрестности точки А0, то
(17)
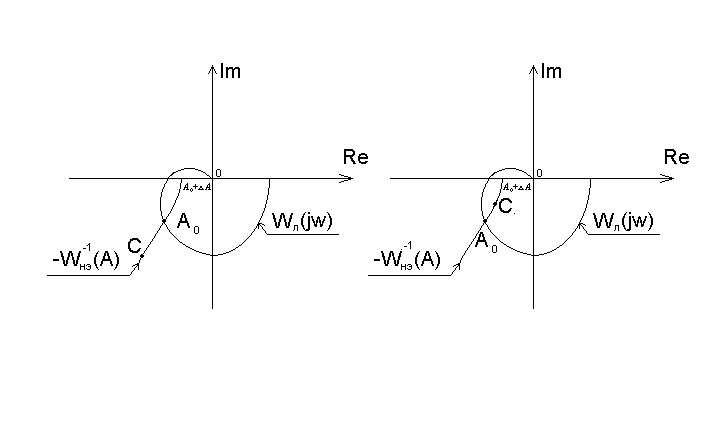
Рисунок 3
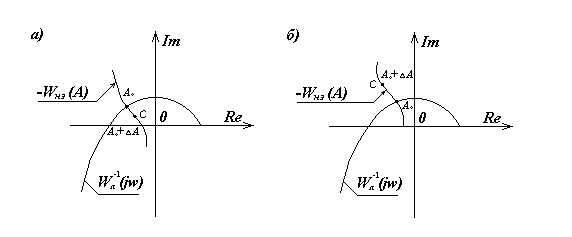
Рисунок 4
В заключение укажем, что для нелинейного элемента с идеальной релейной характеристикой (рисунок 5,а)
(18)
и с релейной характеристикой с зоной нечувствительности (рисунок 5,б)
(19)
Рисунок 5