МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования "южный федеральный университет"
Факультет электроники и приборостроения
Кафедра информационных измерительных технологий и систем
Руководство к практическим работам по курсу
Метрология
Направление 200500.62 “Метрология, стандартизация и сертификация”
Таганрог
2013
© Т.В.Шушкевич, 2013
1 Однократные измерения физической величины. Оценивание погрешности и неопределенности
1.1 Общие сведения
Методика оценивания погрешности и неопределенности приведена в рекомендациях по метрологии Р 50.2.038-2004 "ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений".
Нужно отметить, что этот документ фактически не делает различия между понятиями "погрешность" и "неопределенность", приводя одну и ту же методику для оценки этих величин. По сути, эти рекомендации практически повторяют старый документ МИ 1552-86 "ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений", описывающий методику расчета погрешностей.
Ниже информация из Р 50.2.038-2004 будет использоваться для расчета погрешностей, а расчет неопределенности будет вестись в соответствии с "Руководством по выражению неопределенности".
1.2 Оценивание погрешности результата измерения
1.2.1 Составляющие погрешности результата измерения
Однократное измерение – это измерение, выполненное один раз. Выполнение однократных измерений обычно обосновывают следующими факторами:
– производственной необходимостью (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.);
– возможностью пренебрежения случайными погрешностями.
За результат однократного измерения принимают значение величины, полученное при измерении.
Составляющие погрешности результата измерения должны быть известны до проведения измерения. Предполагают, что известные систематические погрешности исключены (внесены поправки на все известные источники погрешности, имеющие систематический характер).
Составляющими погрешности результата однократного измерения являются погрешности средства измерения (СИ), метода, оператора, а также погрешности, обусловленные изменением условий измерения.
Погрешность результата однократного измерения чаще всего представлена неисключенным остатком систематической погрешности (НСП) и случайными погрешностями.
Характеристикой НСП могут быть:
– границы ±Θ;
– доверительные границы ±Θ(Р).
Характеристикой случайных погрешностей могут быть:
– среднеквадратическое отклонение (СКО) S;
– доверительные границы (доверительный интервал) ±e(Р).
Погрешность СИ определяют на основании их метрологических характеристик, которые должны быть указаны в нормативных и технических документах. Погрешности метода и оператора должны быть определены при разработке и аттестации конкретной методики выполнения измерений (МВИ).
1.2.2 Оценивание неисключенной систематической погрешности результата измерения
НСП результата измерения выражают границами этой погрешности, если среди составляющих погрешности результата измерения в наличии одна НСП.
При наличии нескольких НСП, заданных своими границами ±Θj, доверительную границу НСП результата измерения Θ(Р) (без учета знака) вычисляют по формуле
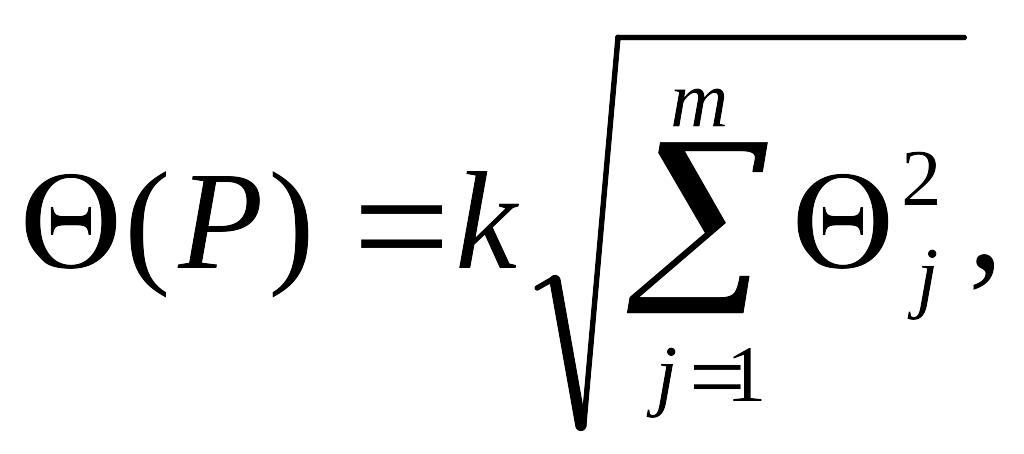(1.1)
где k – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θj.
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих m > 4. Если же число составляющих равно четырем (m = 4), то поправочный коэффициент k ≈ 1,4; при m = 3 k ≈ 1,3; при m = 2 k ≈ 1,2. Более точное значение k для доверительной вероятности Р = 0,99 при числе составляющих m £ 4 в зависимости от соотношения составляющих l определяют по графику [k = f(m, l)] в соответствии с требованиями ГОСТ 8.207.
Погрешность, возникающая при таком суммировании НСП и при нахождении поправочного коэффициента k для доверительной вероятности Р = 0,99 по графику [k = f(m, l)], не превышает 5 %.
При наличии нескольких НСП, заданных доверительными границами (доверительным интервалом) Θj(Рi), доверительную границу НСП результата однократного измерения вычисляют по формуле
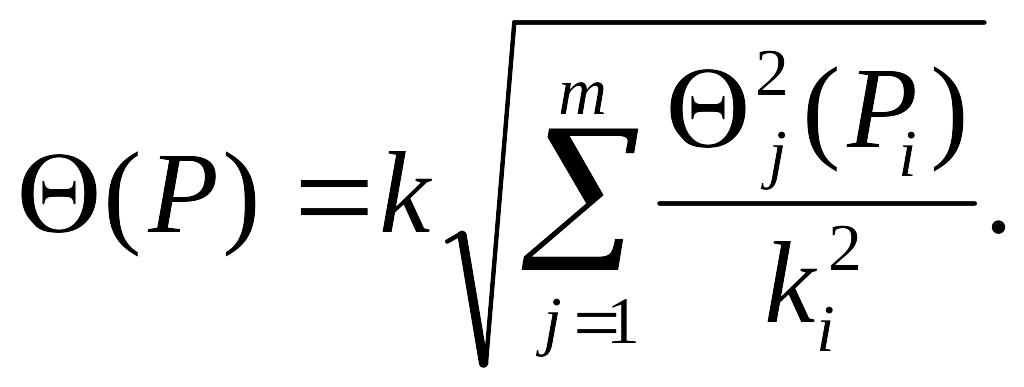
где Θj(Pi) - доверительная граница j-й НСП, соответствующая доверительной вероятности Рi;
k и ki - коэффициенты, соответствующие доверительным вероятностям Р и Рi.
1.2.3 Оценивание случайной погрешности результата измерения
Доверительные границы случайной погрешности результата измерения вычисляют следующим образом.
Если случайные погрешности представлены несколькими СКО Si, то СКО результата однократного измерения S(Ã) вычисляют по формуле
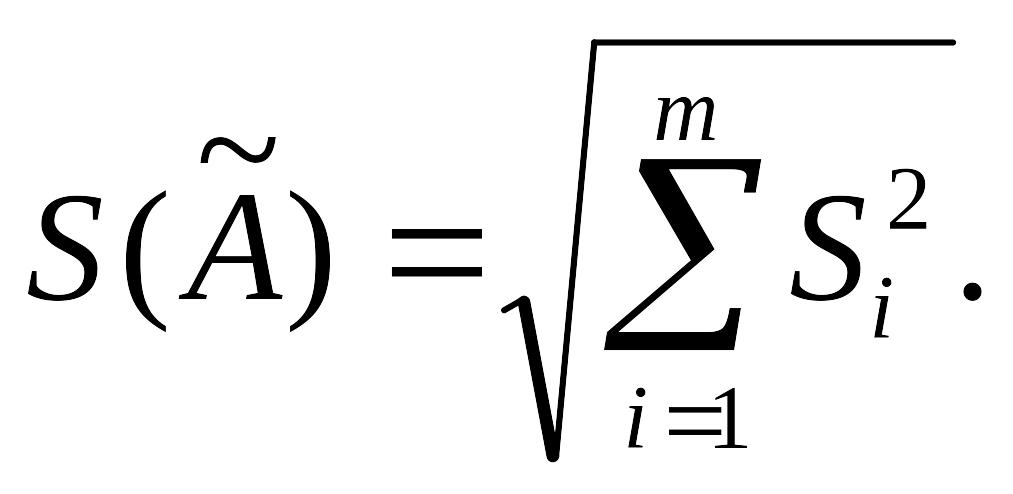
Доверительную границу случайной погрешности результата измерения e(Р) вычисляют по формуле
e(P) = ZP/2S(Ã), (1.2)
где ZP/2 - Р/2 точка нормированной функции Лапласа, отвечающая вероятности Р. При доверительной вероятности Р = 0,95Z0,95/2 принимают равным 2, при Р = 0,99 Z0,99/2 = 2,6.
Если случайные погрешности представлены доверительными границами ei(Р), соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле
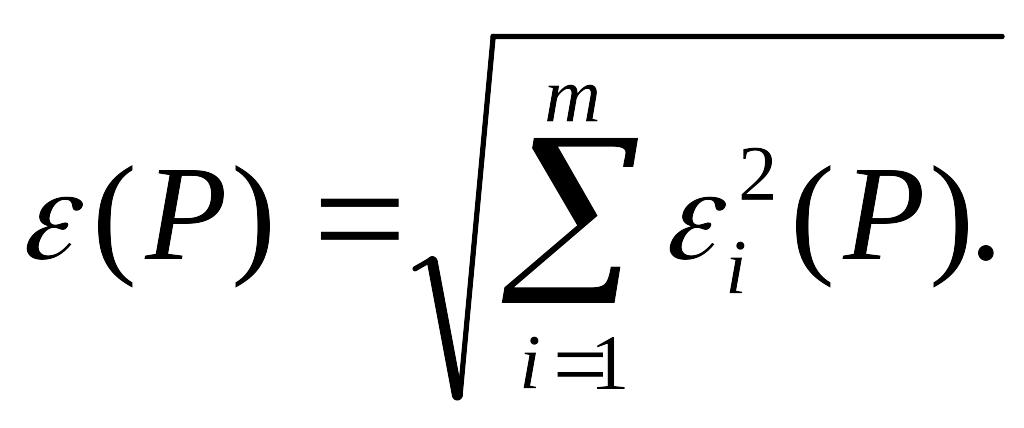
Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО результата измерения по формуле
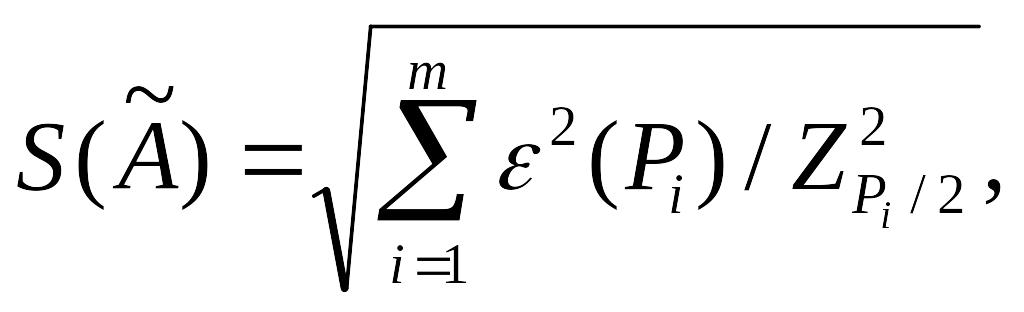
а затем вычисляют доверительные границы случайной погрешности результата измерения по формуле (1.2).