16

Решение типовых задач в непрерывных сау

1. Составление дифференциальных уравнений устройств сау по электрическим и алгоритмическим схемам, получение их офп, переходных h(t) и весовых w(t) функций, афх, ачх, фчх, лачх, лфчх.

1.1. Решение типовых задач для фильтра низких частот (фнч).

Из электрической схемы ФНЧ (рис. 1.1) дифференциальное уравнение запишется в виде:

R

U₁ C R_H U₂

i_С i_Н

(1.1)

Рис. 1.1.

Дифференциальное уравнение ФНЧ в типовой форме запишется:

(1.2)

При d/dt=p, L{U₂(t)}=U₂(p), L{U₁(t)}=U₁(p) получим операторную функцию передачи (ОФП):

(1.3)

где K=R_H/(R+R_H) – коэффициент передачи, а Т=RCK – постоянная времени ФНЧ.

Переходная функция (переходная характеристика) h(t) описывает реакцию ФНЧ на единичное ступенчатое входное воздействие U₁(t)=1[t] при нулевых начальных условиях.

Переходная функция h(t) для ФНЧ получается из решения (интегрирования) его дифференциального уравнения (1.2). Полное решение состоит из суммы общего и частного решения в виде U₂(t)=U_2О(t)+U_2Ч(t). Частное решение представляет собой установившийся процесс при t→∞ в виде U_2Ч(t)=K∙1[t]. Общее решение представляет собой свободное (собственное) движение, которое получается из решения уравнения (1.2) при отсутствии внешнего воздействия U₁(t)=0 и ненулевых начальных условиях в виде где С₁ – постоянная интегрирования, определяемая из начальных условий переходного процесса; p₁ – корень характеристического уравнения Тр+1=0 в виде р₁= –1/Т. Свободная составляющая , а переходный процесс При t=0 и U₂(t)=0 получается С₁=–K∙1[t]. Переходная функция ФНЧ получается в виде:

(1.4)

Весовая функция (функция веса, импульсная переходная характеристика) w(t) представляет реакцию ФНЧ (переходный процесс выходной величины U₂(t)) на входное единичное импульсное воздействие δ(t), называемое дельта-функцией или функцией Дирака. Дельта-функция представляется первой производной от единичной ступенчатой функции , которая равна нулю в любой момент времени t, кроме t=0, где её величина стремится к бесконечности при площади импульса равной единице Функция веса w(t) равна первой производной по времени от переходной функции . Для ФНЧ с ОФП (1.3) переходная функция h(t) и функция веса w(t) вычисляются по (1.4) и (1.5) и имеют вид (рис. 1.2).

(1.5)

Рис. 1.2. Вид переходной функции h(t) и весовой функции w(t) для фильтра низких частот.

Частотные характеристики ФНЧ представляют собой зависимости от частоты ω показателей установившегося процесса выходной величины при синусоидальном входном воздействии с единичным значением амплитуды и изменении частоты ω от 0 до ∞. В линейных ФНЧ выходная величина в установившихся режимах также изменятся по синусоидальному закону, где отношение амплитуд на выходе и входе – есть модуль коэффициента передачи, а – угол фазового сдвига выходной синусоиды относительно входной синусоиды.

Основной частотной характеристикой ФНЧ является амплитудно-фазовая характеристика (АФХ), (комплексный коэффициент передачи, частотная передаточная функция) W(jω), которая получается из ОФП при замене и изменении частоты ω от 0 до ∞ при А₁=1=const с построением АФХ на комплексной плоскости

(1.6)

где U(ω) и jV(ω) – вещественная и мнимая составляющие вектора W(jω), представляющие собой вещественную и мнимую частотные характеристики; – амплитудная частотная характеристика (АЧХ); – фазовая частотная характеристика (ФЧХ). Для ФНЧ с ОФП (1.3) АФХ, АЧХ и ФЧХ описываются уравнениями

(1.7)

(1.8)

, (1.9)

и имеют вид, представленный на рис. 1.3.

В расчетах САУ также широко используются логарифмические амплитудно-частотные характеристики (ЛАЧХ) и логарифмические фазо-частотные характеристики (ЛФЧХ).

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) звена или САУ представляет собой зависимость модуля коэффициента передачи A(ω) в децибелах (дб) от частоты ω входного сигнала в 1/c. ЛАЧХ строится в прямоугольной системе координат (рис. 1.4), где по оси ординат в линейном масштабе указывается коэффициент передачи L(ω) в децибелах

(1.10)

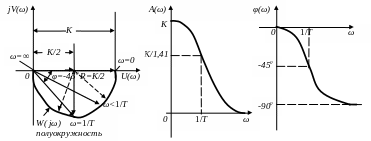
Рис. 1.3. Вид АФХ, АЧХ и ФЧХ фильтра низких частот.

а по оси абсцисс указываются в логарифмическом масштабе (…; 0,01; 0,1; 1; 10; 100; 1000;…) значения частоты ω в 1/c либо значения десятичного логарифма lg(ω/ω₀) отношения частоты ω к частоте ω₀, принятой за единицу измерения (например, 1/c).При этом по оси абсцисс откладываются равномерные отрезки, образующие декады единиц изменения частоты, на которых частота изменяется в 10 раз (рис. 1.4). Один децибел равен 1/10 бела. Один бел равен десятичному логарифму отношения мощностей сигналов на выходе и входе звена или САУ, либо пропорциональных им отношений квадратов напряжений, токов, моментов, скоростей и других однотипных величин на выходе и входе 1 бел=lg(P₂/P₁)=lg(U₂/U₁)². Поэтому в (1.10) введен множитель 20=10 ∙2, где 10 выражает перевод белов в децибелы, а 2 получается при логарифмировании квадрата отношения выходной и входной величин.

ЛАЧХ для ФНЧ с ОФП (1.3) с учетом (1.8) и (1.10) запишется:

(1.11)

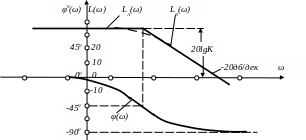
ЛАЧХ ФНЧ по (1.11) имеет две асимптоты:

а) при ω<1/T величина w²Т²<<1, сумма (1+^T²)» и первая асимптота ЛАЧХ L_А(ω)=20lgK представляется горизонтальной прямой (рис. 1.4);

б) при ω>1/T величина w²Т²>>1, сумма (1+w²Т²)»w²Т² и вторая асимптота ЛАЧХ L_Б(ω)=20lgK–20lgωT представляет прямую с наклоном минус 20 дб /дек к оси абсцисс (рис. 1.4).

Эти асимптоты пересекаются при частоте сопряжения ω_С=1/T, при которой асимптотическая ЛАЧХ превышает точную ЛАЧХ по (1.11) (показана пунктиром на рис. 1.4) на очень малую величину которой можно пренебречь и считать, что ЛАЧХ (рис. 1.4) состоит из горизонтальной и наклонной асимптот.

Логарифмическая фазо-частотная характеристика (ЛФЧХ) строится в прямоугольной системе координат, где по оси ординат в линейном масштабе указывается угол фазового сдвига φ() в угловых градусах или радианах, а по оси абсцисс в логарифмическом масштабе указывается частота ω в 1/c. Обычно ЛАЧХ и ЛФЧХ строятся в общей прямоугольной системе координат для удобства расчетов САУ.

ЛФЧХ φ(ω) для ФНЧ с ОФП (1.3) описывается тем же уравнением (1.9), что и для ФЧХ, но ЛФЧХ строится в логарифмической шкале частот совместно с ЛАЧХ (рис. 1.4).

90⁰ дб ω_c= 1/T

30

0,01 0,1 1 10 100 1000 1/c

-2 ­-1 0 1 2 3 lg ω/ω₀

Рис. 1.4. Вид ЛАЧХ и ЛФЧХ для фильтра низких частот (ФНЧ).