Средняя гармоническая взвешенная. Рассмотрим вариант, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель.
Валовой сбор и урожайность зерновых культур
Область |
Валовой сбор, тыс. т |
Урожайность, ц/га |
Курганская Свердловская Тюменская Челябинская |
1088,3 603,5 1171,5 1050,7 |
10,9 12,1 17,5 8,8 |
Средняя урожайность любой сельскохозяйственной культуры по нескольким территориям, агрофирмам, крестьянским хозяйствам и т.п. может быть определена только на основе следующего исходного соотношения:
Общий валовой сбор мы получим простым суммированием валового сбора по областям. Данные же о посевной площади в таблице отсутствуют, но их можно получить, разделив валовой сбор по каждой области на урожайность. С учетом этого определим искомую среднюю по формуле средней гармонической взвешенной, предварительно переведя для сопоставимости тонны в центнеры:
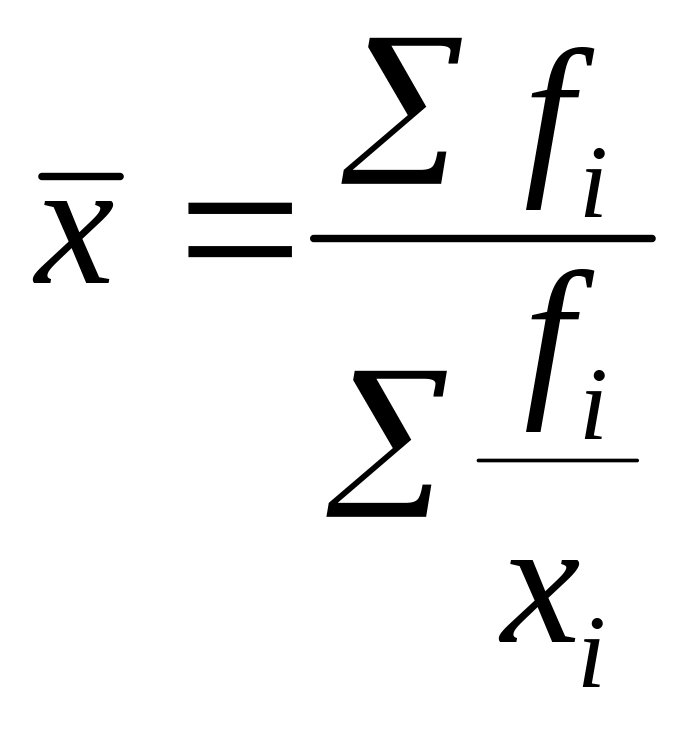
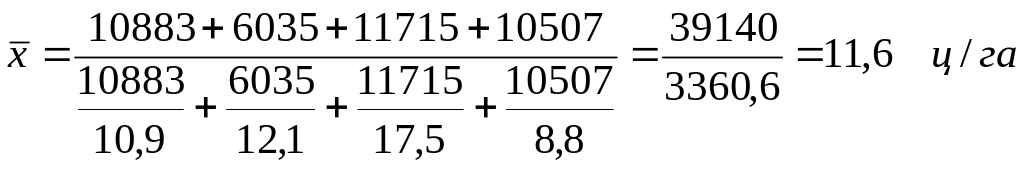
Таким образом, общая посевная площадь зерновых культур составила 3360,6 тыс.га, а средняя урожайность - 11,6 ц с 1 га.
Средняя гармоническая невзвешенная используется значительно реже, имеет следующий вид:
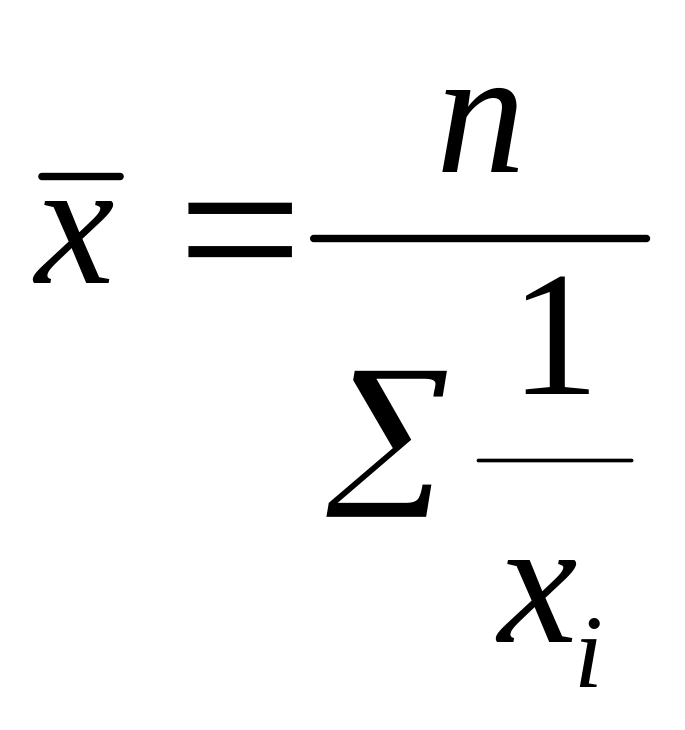
3. Средняя геометрическая. Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
- средняя
геометрическая невзвешенная:
- средняя
геометрическая взвешенная:
4. Средняя квадратическая. Используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения.
-
средняя
квадратическая невзвешенная:
-
средняя
квадратическая взвешенная:
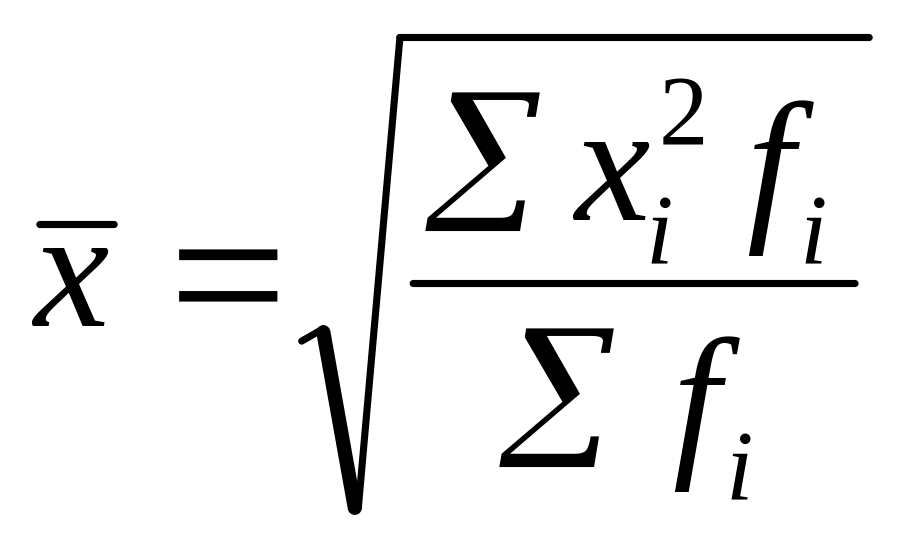
В статистической практике также находят применение степенные средние 3-го и более высоких порядков.
Известно, что степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. И чем больше показатель степени k, тем больше и величина соответствующей средней:
Это свойство степенных средних возрастать с повышением показателя степени называется мажорантностью средних.