Глава 10

Алгоритми нахождення на графах найкоротших шляхів

Завдання відшукання на графі найкоротшого шляху має численні практичні додатки. З рішенням подібної завдання % доводиться зустрічатися в техніці зв'язку (наприклад, при телефонізації населених пунктів), на транспорті (при виборі оптимальних маршрутів доставки вантажів), в мікроелектроніці (при проектуванні топології мікросхем) і т.д. Шлях між вершинами р і 3 графа вважається найкоротшим, якщо вершини г і 3 з'єднані мінімальним числом ребер (випадок не зваженого графа) або якщо сума ваг ребер, що з'єднують вершини г і з мінімальний (для зваженого графа). Важливим показником алгоритму є його ефективність. Стосовно до поставленої задачі ефективність алгоритму може залежати в основному від двох параметрів графа: числа його вершин і числа ваг його ребер. Розглянемо три алгоритму для визначення найкоротшого відстані між вершинами графа: побудова дерева рішень, метод динамічного програмування і метод Дейкстри.

10.1.

Побудова дерева рішень

Метод побудови дерева рішень зазвичай використовується для знаходження найкоротшого шляху в орієнтованому графі, при цьому від вихідного графа переходять до матриці суміжності. Потім переглядають рядка матриці едомської, і граф послідовно «розшаровується» дерево рішень. Приклад 1. Знайти найкоротший шлях від вершини 1 до вершини у графі 6, зображену на рис. 10.1.

В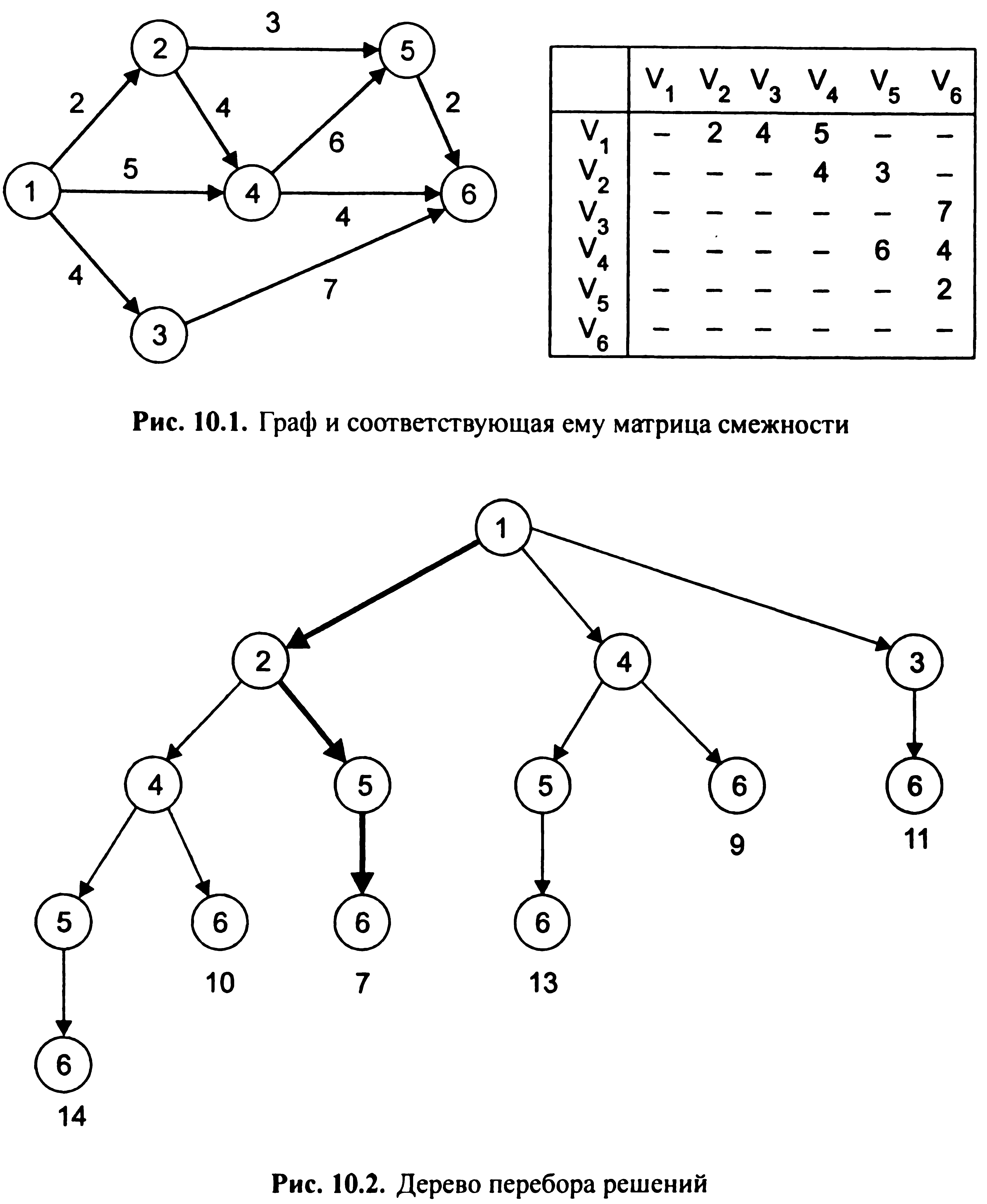 матриці суміжності ваг даного графа символ «прочерк» означає відсутність зв'язку між відповідними вершинами.

Повне дерево перебору, побудоване за цим алгоритмом, зображене на рис. 10.2. З рис. 10.2 неважко бачити, що найкоротший шлях з вершини 1 у вершину 6 дорівнює 7 і має вигляд(1 - 2 - 5 - 6). Приклад 2. Знайти найкоротший шлях від вершини 1 до вершини б в орієнтованому графі, зображену на рис. 10.3.

П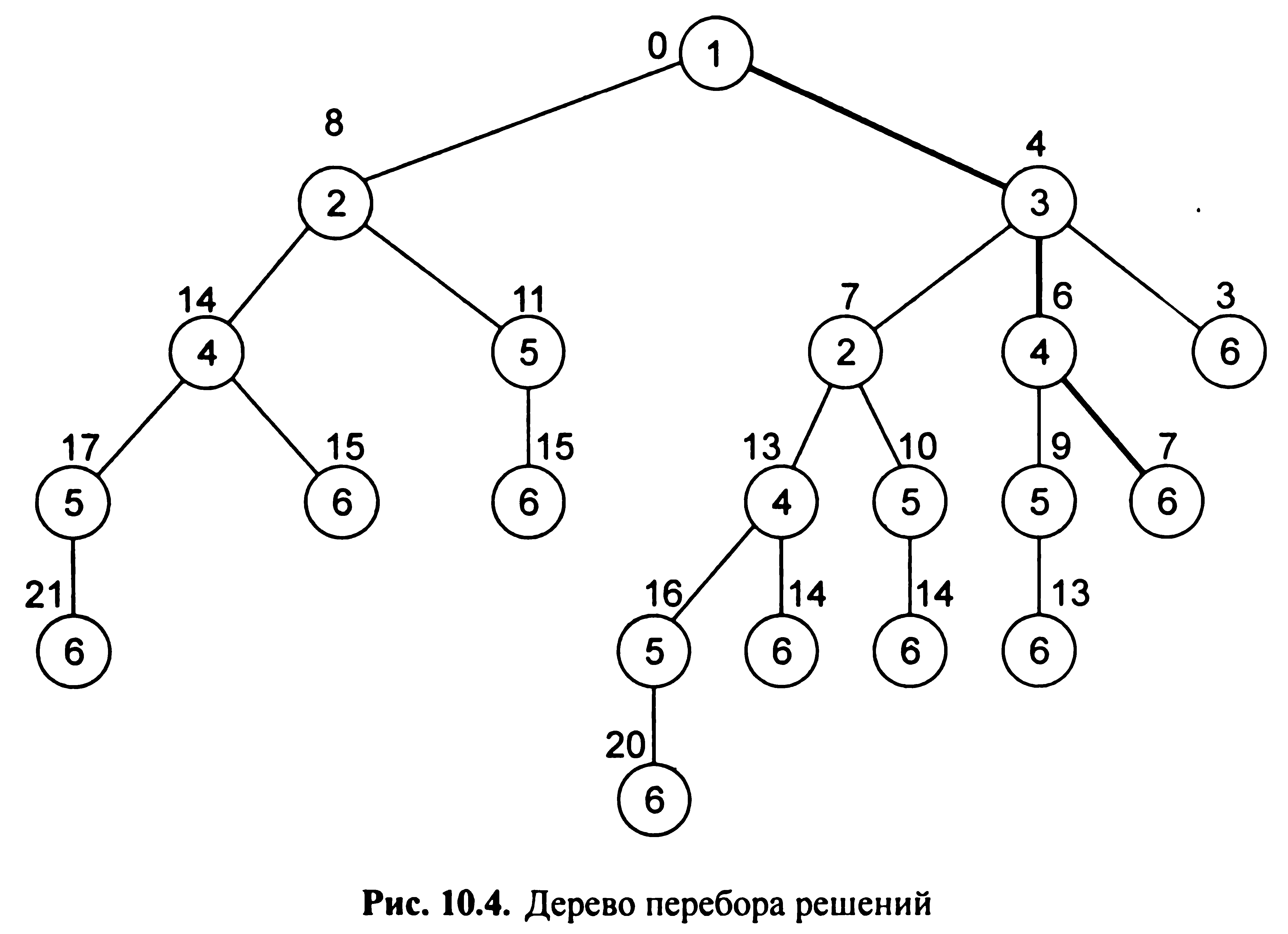 ослідовно переглядаємо рядка матриці едомської і будуємо дерево рішень. Повне дерево перебору зображено на рис. 10.4

Дерево рішень показує всі можливі шляхи. Є дев ’ ять варіантів шляхів від першої до шостої вершини. Найкоротший шлях дорівнює V1 - Vз - V4 - V6.

10.2.

Метод динамічного програмування

Метод динамічного програмування заснований на покрокової оптимізації цільової функції, де в якості цільової функції може бути вартість, ресурсні витрати, фінансово-економічні витрати, а також найкоротші шляхи. Розглянемо приклад топологічної оптимізації. Приклад 1. Нехай дана карта місцевості (мал. 10.5). Розбиваємо карту місцевості координатної сітки. Крок сітки вибирається виходячи з умови точності. Вузли координатної сітки вважаємо вершинами графа.

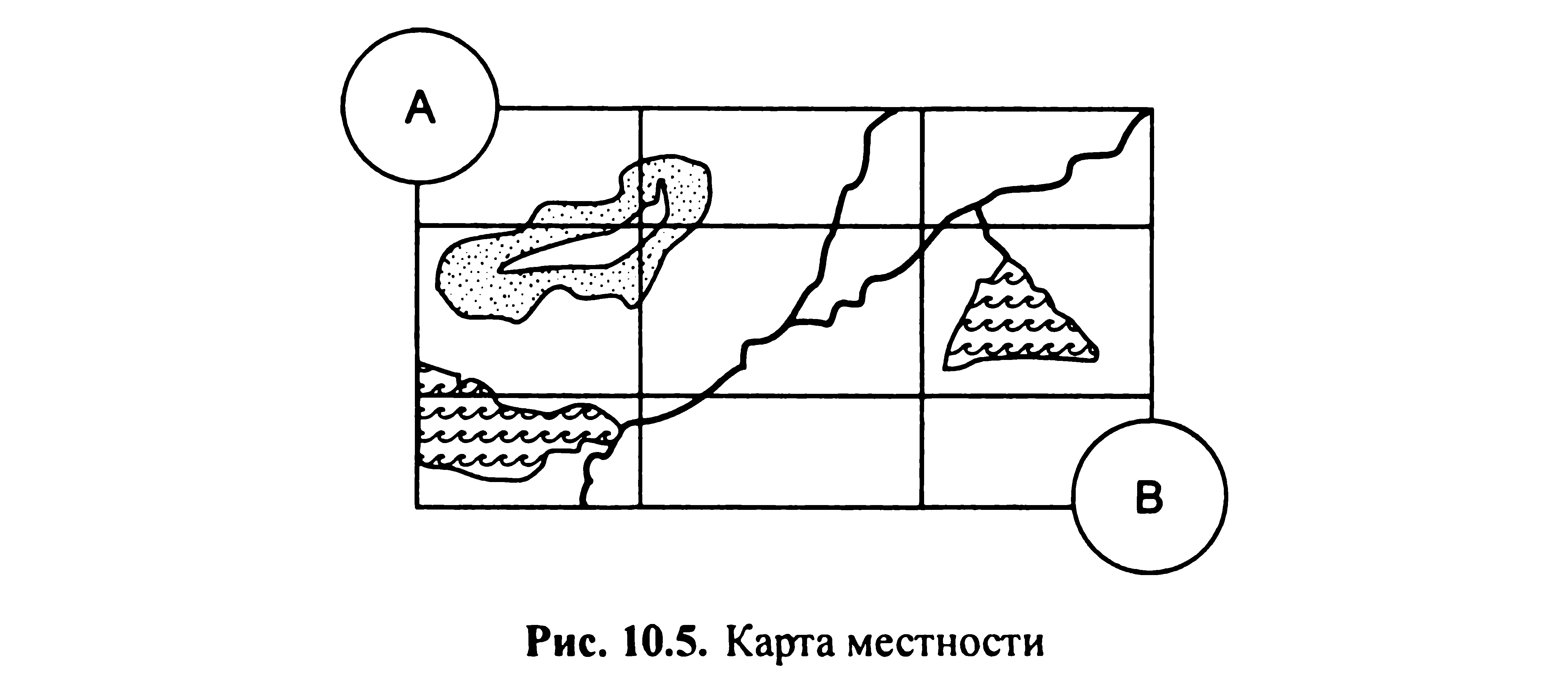
Проставляємо ваги ребер виходячи з того, яка мета переслідується. Побудова шляху здійснюється з кінцевої вершини в початкову виходячи з таких пріоритетних напрямків: вниз і вправо (при русі до кінцевої вершині). На першому етапі руху до кінцевої вершини У вимушені, тобто вниз і вправо (мал. 10.6, а). На наступних кроках напрямок руху визначається оптимізацією довжин шляхів (мал. 10.6, б). В результаті виконання операцій визначається довжина шляху між вершинами (22 одиниці) і траєкторія руху (по стрілках) - мал. 10.6, в. Метод динамічного програмування розглядає багатостадійні процеси прийняття рішення. При постановці завдання

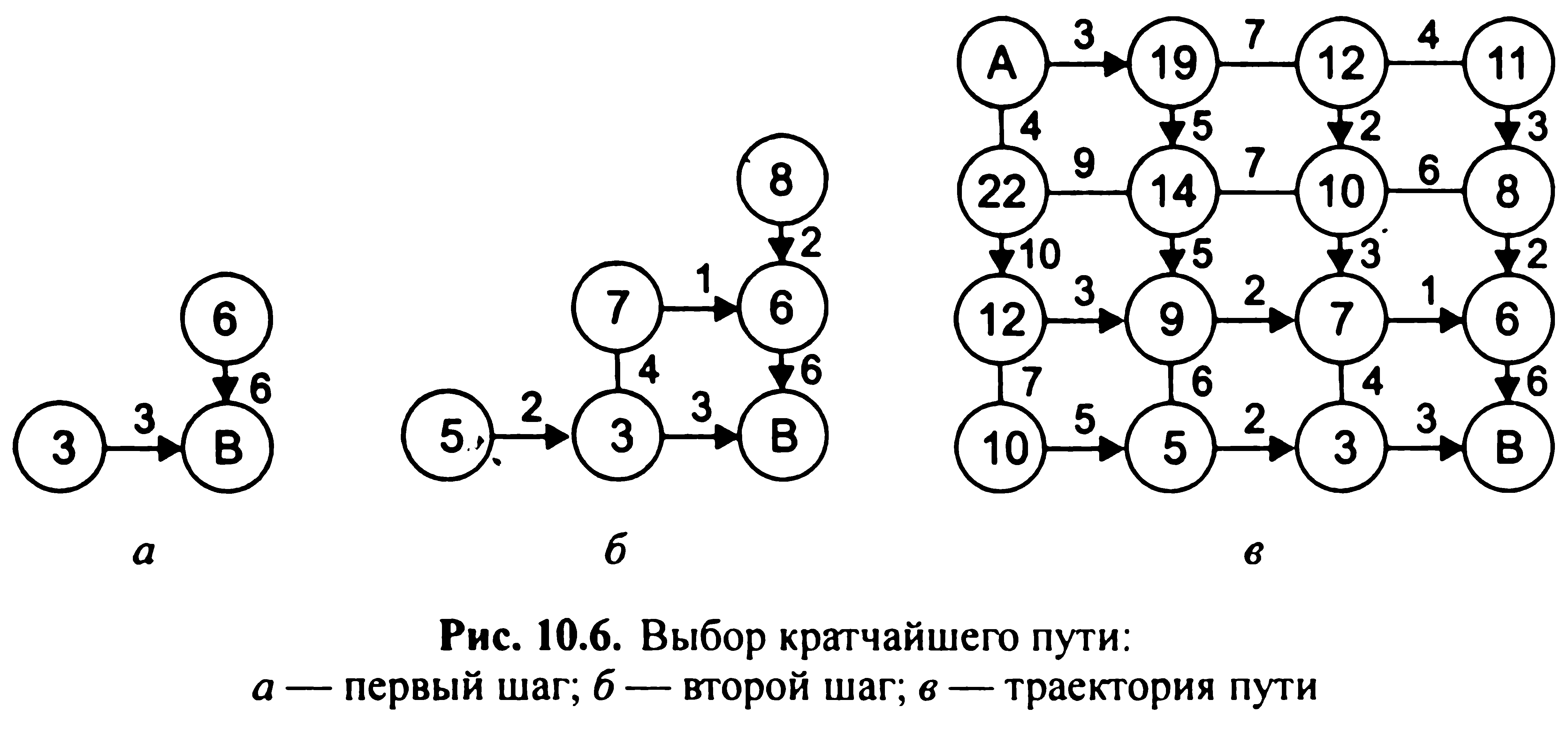
динамічного програмування формується деякий критерій. Процес розбивається на стадії (кроки), в яких приймаються рішення, які призводять до досягнення спільної мети. Таким чином, метод динамічного програмування - метод покрокової оптимізації. Введемо функцію що визначає мінімальну довжину шляху з початкової в вершину i. Позначимо через Sij довжину шляху між вершинами i та j, a fj - найменшу довжину шляху між вершиною j і початкової вершиною. Вибираючи як i таку вершину, яка мінімізує суму Sij+fj отримуємо рівняння

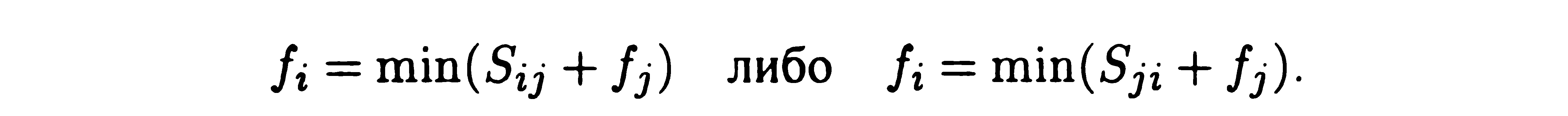
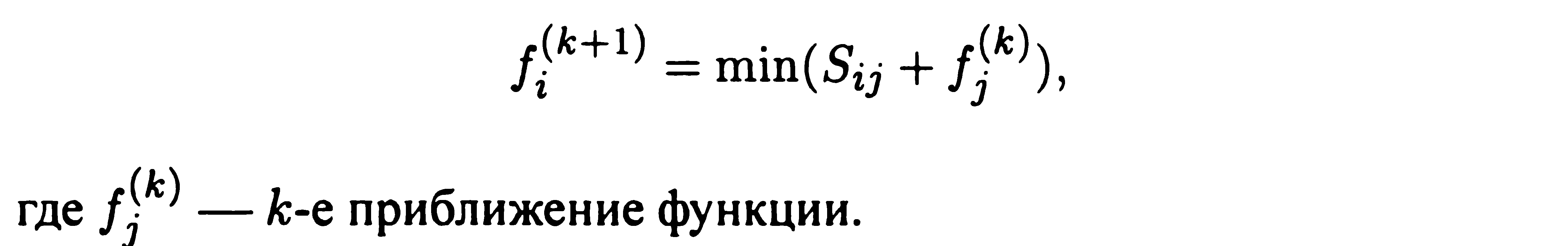Труднощі рішення даного рівняння полягає в тому, що невідома функція входить в обидві частини рівності. У такій ситуації доводиться вдаватися до класичним методом послідовних

наближень (ітерацій), використовуючи рекурентну формулу:

М ожливий інший підхід до рішення поставленої задачі за допомогою методу стратегій. При русі з початкової точки i в кінцеву k виходить наближення — довжина щляху між точками i,k.

Наступне наближення - пошук рішення в класі дволанкових ламаних. Подальші наближення шукаються у класі триланкових, четырехзвенных та інших ламаних. Приклад 2. Знайти, використовуючи метод динамічного програмування, найкоротший шлях між вершинами 1 і 6 у графі на рис. 10.7.

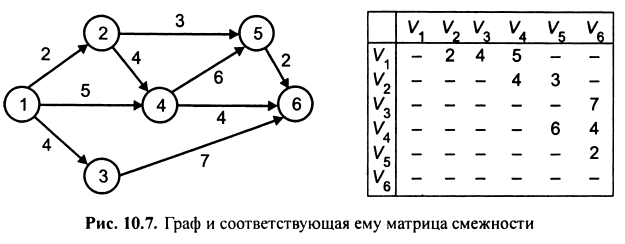
З останніх співвідношень знаходимо, що мають місце такі мінімальні значення: F6= 5, f5 = 7. Таким чином, в результаті виконання першого етапу алгоритму знайдено, що найкоротший шлях з вершини 1 у вершину 6 дорівнює 7. На другому етапі алгоритму буде знайдена послідовність вершин, через які проходить обчислений мінімальний шлях. Для цього необхідно знайти послідовність тих функцій, яким відповідає вибраний мінімум. Для функції f6 мінімум обчислювався через значення функції f5. У свою чергу, мінімум функції f5 був обчислений через мінімальне значення функції f2, а функції f2 - через мінімальне значення функції f1. Отже, «відпрацювання назад» від кінцевої вершини 6 шуканого шляху до його початкової вершини 1 дозволяє вказати послідовність прохідних при цьому вершин графа-(1 - 2 - 5 - 6).

Приклад 3. Визначити найкоротший шлях з вершини 1 у вершину 10 для графа, представленого на рис. 10.8

Рис. 10.8. Зважений орієнтований граф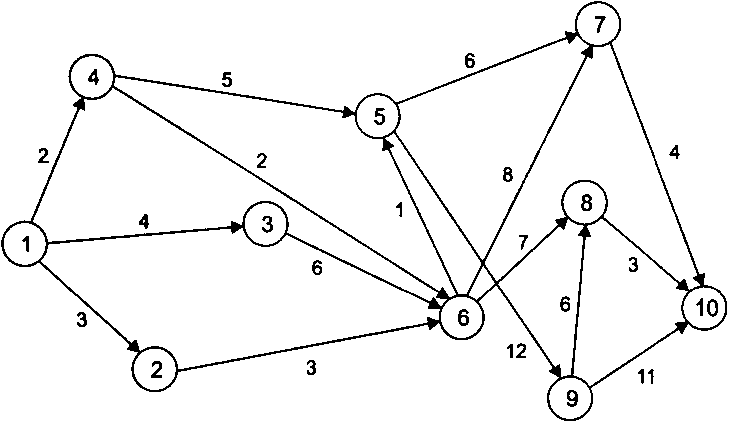

Початкові умови: f1 = 0.

Знаходимо послідовно значення функції fi (в умовних одиницях) для кожної вершини орієнтованого графа:

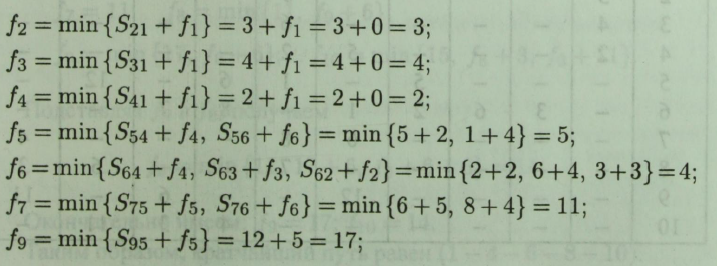
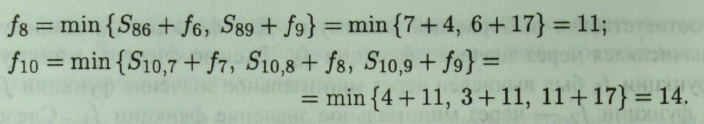
Д овжина найкоротшого шляху становить 14 умовних одиниць. Для вибору оптимальної траєкторії руху слід здійснити перегляд функцій fi в зворотномупорядку, тобто з f10. Нехай fi = f10. В даному випадку

О тримуємо, що 3 + f8 = 14, тобто fi = f8. Значить, з вершини 10 слід перейти до вершини 8. Маємо fi = f8. Розглянемо функцію

т.е. fi = f6 и т.д.

Таким чином, отримуємо найкоротший шлях від вершини 1 до вершини 10:

(1 – 4 – 6 - 8 - 10).

Розглянутий метод визначення найкоротшого шляху може бути поширений і на неорієнтовані графи.

Приклад 4. Для графа (рис. 10.8) знайти найкоротший шлях від вершини 1 до вершини 10, розглядаючи граф як неорієнтований. Матриця суміжності ваг графа в цьому випадку має вигляд:

	1	2	3	4	5	6	7	8	9	10
1	—	3	4	2	—	—	—	—	—	-
2	3	—	—	—	—	3	—	—	—	—
3	4	—	—	—	—	6	—	—	—	-
4	2	—	—	—	5	2	-	—	—	—
5	—	—	—	5	—	1	6	—	12	—
6	—	3	6	2	1	—	8	7	-	—
7	—	—	—	—	6	8	—	—	—	4
8		—	—	—	—	7	—	—	6	3
9	—	—	—	—	12	—	—	6	—	11
10	—	—	-	-	—	-	4	3	11	—

Запишемо вираз для функції f *:

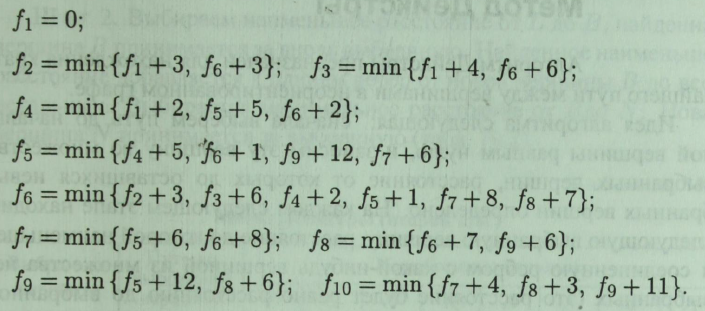
Зазначені цільові функції являють собою систему лінійних алгебраїчних рівнянь (в прикладі є 10 рівнянь і 10 невідомих).

Розглянемо один з варіантів її вирішення, враховуючи, що f1 = 0. Тоді маємо:

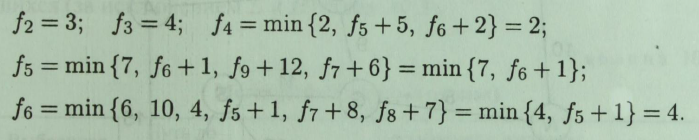
Підставивши вираз для f6 в f5, отримаємо

Тоді

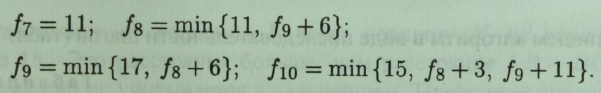
Підставляючи f9 в f8, отримуємо

Остаточно маємо: f9 = 17; f10 = 14.

Таким чином, найкоротший шлях дорівнює (1-4-6 - 8 - 10).

10.3. Метод Дейкстри

Алгоритм Дейкстри призначений для знаходження найкоротшого шляху між вершинами в неорієнтованому графі.

Ідея алгоритму наступна: спочатку виберемо шлях до початкової вершини рівним нулю, і заносимо цю вершину в безліч обраних вершин, відстань від яких до решти невибраних вершин визначено. На кожному наступному етапі знаходимо наступну вибрану вершину, відстань до якої найменше і сполучену ребром з якою-небудь вершиною з множини не-обраних (це відстань буде рівна відстані до обраної вершини плюс довжина ребра).

Приклад 1. Знайти найкоротший шлях на графі від вершини L до вершини D (рис. 10.9).

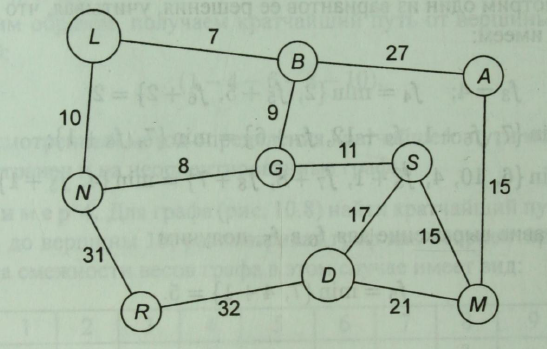
Рис. 10.9. Зважений неорієнтовані граф

Запишемо алгоритм у вигляді послідовності кроків (табл. 10.1).

Крок 1. Визначаються відстані від початкової вершини L до всіх інших.

Крок 2. Вибираємо найменшу відстань від L до В, знайдена вершина В приймається за знову обрану. Знайдене найменша відстань додається до довжин ребер від нової вершини В до всіх інших. Вибирається мінімальна відстань від B до N. Нова вершина N приймається за обрану (табл. 10.2).

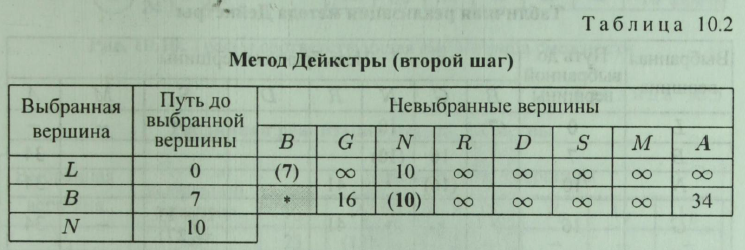
Для наочності надалі замість знака оо будемо ставити знак «-».

Крок 3. Визначаються відстані від вершини N до всіх залишилися (за винятком L і В) (табл. 10.3).

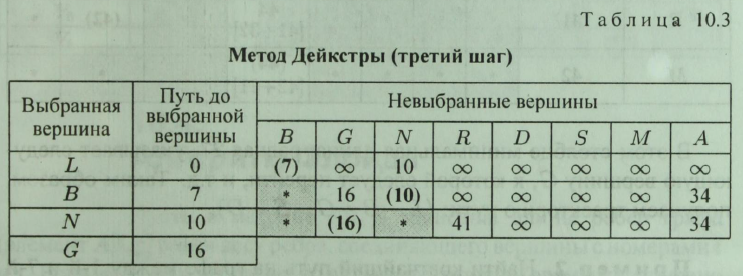
Відстань від вершини L через вершину N до вершини G дорівнює 18. Це відстань більше, ніж відстань LB + BG = 16, тому воно не враховується в подальшому. Продовжуючи аналогічні побудови, побудуємо табл. 10.4 (величини, зазначені в квадратних дужках, не враховуються). Таким чином, знайдена дли на найкоротшого шляху між вершинами L і D (44 умовні одиниці).

Траєкторія шляху визначається наступним чином. Здійснюємо зворотний перегляд від кінцевої вершини до початкової. Переглядаємо стовпець, відповідний вершині, знизу вгору і фіксуємо

перша поява мінімальної величини. У стовпці, відповідному вершині D, вперше мінімальна довжина 44 з'явилася знизу в четвертому рядку. У цьому рядку вказана вершина S, до якої слід перейти, тобто наступним потрібно розглядати стовпець, відповідний вершині S.

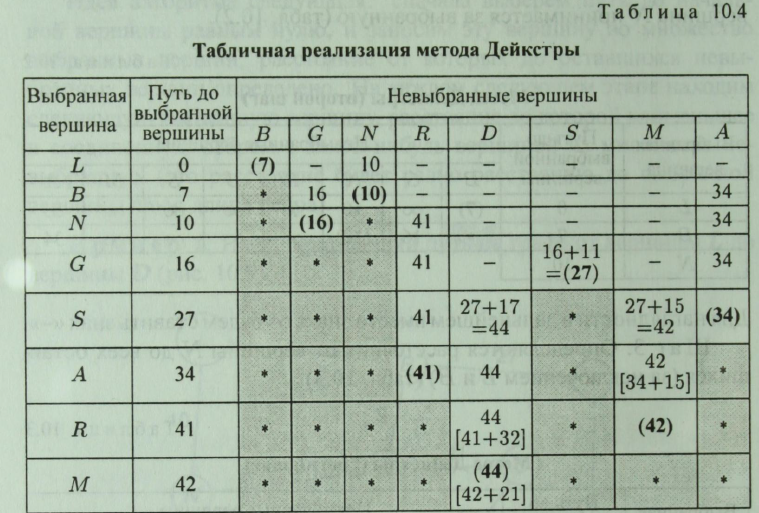
У цьому стовпці мінімальна довжина, рівна 27, вказує наступну вершину G, до якої слід перейти, і т.д. Таким чином, отримуємо траєкторію шляху: (LBGSD).

Приклад 2. Знайти найкоротший шлях на графі між 1-й і 7-й вершинами (рис. 10.10).

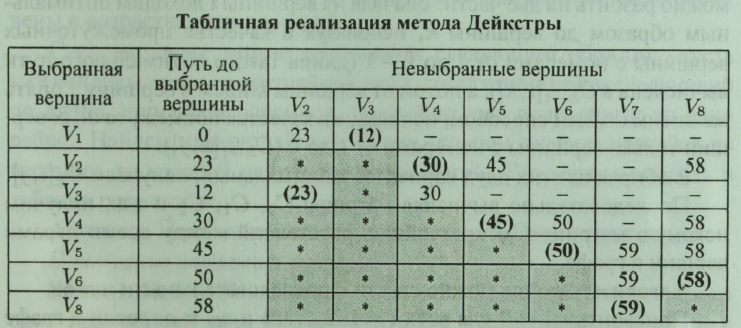
Визначаємо наступну вибрану вершину, відстань до якої найменше, і сполучену ребром з однією з вершин, що належать безлічі невибраних. Це відстань буде рівна відстані до обраної вершини плюс довжина ребра (табл. 10.5).

Здійснюємо зворотний перегляд від кінцевої вершини до початкової. Переглядаємо стовпець, відповідний вершині, знизу вгору і фіксуємо перша поява мінімальної величини.

Найкоротший шлях при цьому буде рівний (V7 - V5 - V2 - Vi).

Таблица 10.5

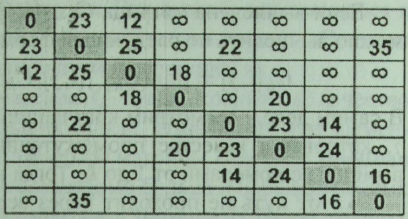
Рис. 10.10. Граф и соответствующая ему матрица смежности

10.4. Алгоритм Флойда

Нехай в матриці A [i, j] записані довжини ребер графа (елемент А [i, j] дорівнює вазі ребра, що з'єднує вершини з номерами i і j. Якщо ж такого ребра немає, то у відповідному елементі записано деякий дуже велике число. Побудуємо нові матриці Ck [i, j] (к = 0, ..., N). Елемент матриці Ck [i, j] буде дорівнювати мінімально можливій довжині такого шляху iз i в j, що в якості проміжних вершин у цьому шляху використовуються вершини з номерами від 1 до k, тобто розглядаються шляхи, які можуть проходити через вершини з номерами від 1 до k, але свідомо не проходять через вершини з номерами від до k + 1 до N. У матрицю записується довжина найкоротшого з таких шляхів. Якщо таких шляхів не існує, записується той же велике число, яким позначається відсутність ребра.

Якщо обчислена матриця , то елементи матриці Ck [i, j] можна обчислити за такою формулою

У самому справі, розглянемо найкоротший шлях з вершини i у вершину j, який у якості проміжних вершин використовує тільки вершини з номерами від 1 до k. Тоді можливо два випадки:

• цей шлях не проходить через вершину з номером k. Тоді його проміжні вершини - це вершини з номерами від 1 до до k - 1. Але тоді довжина цього шляху вже обчислена в елементі

• цей шлях проходить через вершину з номером оскільки Але тоді його можна розбити на дві частини: спочатку з вершини i доходимо оптималь ним чином до вершини k, використовуючи в якості проміжних вершини з номерами від 1 до k - 1 (довжина такого оптимального шляху обчислена в ), а потім від вершини k йдемо в вершину j знову ж оптимальним способом, використовуючи в якості проміжних вершин тільки вершини з номерами від 1 до k .

Вибираючи з цих двох варіантів мінімальний, отримуємо Ck [i, j].

Послідовно обчислюючи матриці і т.д., отримаємо шукану матрицю CN найкоротших відстаней між усіма парами вершин у графі.

Алгоритм Флойда можна звести до послідовності кроків.

Присвоїти для всіх і , якщо в графі відсутня дуга

Присвоєння початкових значень.

Крок 1. Присвоїти k = 0.

Крок 2. k = k + 1.

Крок 3. Для всіх , таких, що , і для всіх , таких,

що

Перевірка на закінчення.

Ш а р 4. Якщо k = n, то матриця дає довжини всіх найкоротших шляхів. Зупинка. Інакше перейти до кроку 2.

10.5. Алгоритм Йена

Нехай граф заданий матрицею . Вершина S обрана як початкова. Знайдемо довжини k найменших шляхів до кожної вершини від вершини s (ребра в одному шляху можуть повторюватися неодноразово),

за умови, що ці шляхи існують. Результат буде зберігатися в матриці В розміром , де N - кількість вершин. Елемент масиву B [i, j] дорівнює j-му по довжині шляху до вершини i.

Для кожної вершини в масиві C будемо зберігати кількість вже знайдених до неї найменших шляхів. Спочатку всі елементи масиву С дорівнюють нулю. Всі елементи матриці В робимо рівними небудь великий константі, завідомо більшою всіх можливих шляхів. Під час виконання алгоритму в матриці В будемо зберігати кращі k шляхів до кожної вершини, знайдені під час виконання, при цьому перші C[i] шляхів для вершини i вже знайдені остаточно (елементи матриці В - B [i, 1], B [i , 2], ..., B [i, k] для всіх i впорядковані у зростаючому порядку).

Отже, можна діяти наступним чином: нехай уже знайдені якісь найкоротші шляхи, тоді щоб знайти наступний по довжині, спробуємо подовжити кожен з вже отриманих на одне ребро. Знайдемо найліпший з них, причому закінчується на вершину, до якої знайдено менше до шляхів. Його можна вносити в таблицю результату.

Алгоритм Йена можна звести до послідовності кроків.

Присвоєння початкових значень.

Крок 1. Знайти . Присвоїти k = 2. Якщо існує тільки один найкоротший шлях , включити його в список і перейти до кроку 2. Якщо таких шляхів кілька, але менше, ніж К, включити один і них в список , а інші в список . Перейти до кроку 2. Якщо існує К або більше найкоротших шляхів , то задача вирішена. Зупинка.

Знаходження відхилень.

Крок 2. Знайти усі відхилення найкоротшого шляху для всіх виконуючи для кожного i кроки з 3-го по 6-й.

Крок 3. Перевірити, чи збігається подпуть, утворений першими i вершинами будь-якого з шляхів . Якщо так, то привласнити з ; інакше нічого не змінювати. (При виконанні алгоритму вершина позначається s.)

Крок 4. Знайти найкоротші шляхи , виключаючи з розгляду вершини . Якщо існує кілька найкоротших шляхів, то взяти в якості один з них.

Крок 5. Побудувати і помістити Р в список .

Крок 6. Замінити елементи матриці ваг, змінені на кроці їх початковими значеннями і повернутися до кроку 3.

Вибір найкоротших відхилень.

Крок 7. Знайти найкоротший шлях в списку . Позначити цей шлях і перемістити його з в . ЯКЩО k = К, то зупинка. Список - список k-найкоротших шляхів.

Якщо k <К, то привласнити , перейти до кроку 2. Якщо в мається більш ніж один найкоротший шлях , то помістити в будь-який з них і продовжувати обчислення до тих пір, поки збільшене на h число шляхів, що вже знаходяться в , не співпаде з K або не перевищить його. Тоді - зупинка.

10.6.Алгоритм Беллмана – Форда

Нехай в матриці A [i, j] записані довжини ребер графа. Знайдемо найкоротший відстані від заданої вершини s до всіх інших вершин графа. Алгоритм Беллмана - Форда вирішує цю задачу навіть при наявності ребер негативного ваги. Позначимо через найменшу вартість проїзду з s в і менш ніж з до пересадками:

Шуканим відповіддю є для всіх i = 1 .. n.

Щоб знайти не тільки довжини найменших шляхів до всіх вершин, але й самі ці шляхи, використовуємо наступний прийом. Паралельно з обчисленням масиву х будемо обчислювати матрицю D [i, j]. Якщо між вершинами s і j існує шлях, то в елементі масиву D [j, 0] буде зберігається кількість вершин в цьому шляху, а ланцюжок вершин, складена з елементів з D [j, 1] по D [j, D [j, 0]], буде цим самим шляхом. Шлях до вершини s містить єдину вершину (D [s, 0] = 1;D [s, l] = s). Для обчислення матриці D буде потрібно доповнити текст процедури:

Обозначим через наименьшую стоимость проезда из s в i менее чем с к пересадками. Тогда

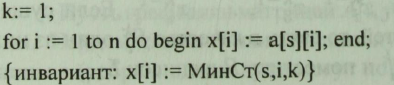
выполняется такое соотношение:

Контрольні питання

1. У чому особливість побудови дерева рішень? «

2. Що показує дерево рішень?

3. Яким чином використовується метод оптимізації для визначення найкоротшого шляху по карті місцевості?

4. У рішенні яких прикладних задач використовуються алгоритми визна ¬ ділення в графі найкоротших відстаней між заданими верші ¬ нами?

5. Чи може бути застосований алгоритм Дейкстри до визначення кратчай ¬ дової відстані в орієнтованому графі?

6. Як працює алгоритм Дейкстри?

7. Як працює алгоритм динамічного програмування застосуй ¬ тельно до задачі визначення в графі найкоротших відстаней між вершинами?

8. У чому особливість алгоритму Флойда?

9. У чому особливість алгоритму Йєна?

10. Вкажіть основний принцип побудови алгоритму Беллмана - Форда.