
Сортування вибором
Сортування вибором полягає в тому, що спочатку в невпорядковане списку вибирається і відділяється від інших найменший елемент. Після цього початковий список виявляється зміненим. Змінений список приймається за вихідний і процес продовжується до тих пір, поки всі елементи не будуть обрані. Очевидно, що вибрані елементи утворюють впорядкований список. Наприклад, потрібно знайти мінімальний елемент списку {5, 11, 6, 4, 9, 2, 15, 7}. Процес вибору показаний на рис. 5.2, де в кожному рядку виписані порівнювані пари. Вибрані елементи з меншою вагою обведені кружком. Неважко бачити, що число порівнянь відповідає на малюнку числу рядків, а число переміщень - кількістю змін вибраного елемента.
{5,11,6,
4, 9, 2,15,7}
511
Рис. 5.2. Сортировка
выбором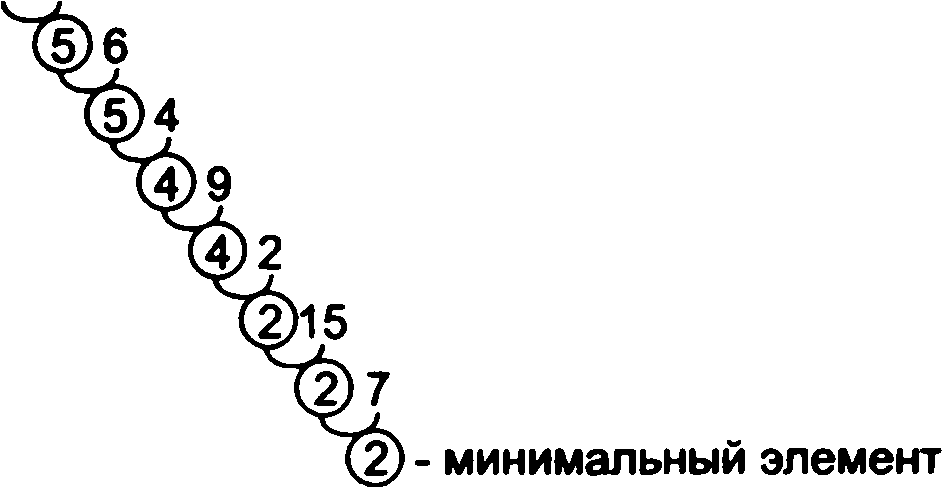
Обраний у вихідному списку мінімальний елемент розміщується на призначеному йому місці кількома способами. • Мінімальний елемент після р-го перегляду переміщується на г-е місце нового списку (i=1,2,...,n), а у вихідному списку на місце обраного елемента записується якесь дуже велике число, що перевершує за розмірами будь-який елемент списку. При цьому довжина заданого списку залишається постійною. Змінений таким чином список можна приймати за вихідний. • Мінімальний елемент записується на i-е місце вихідного списку (i = 1,2,..., n), а елемент з i-го місця на місце обраного. При цьому очевидно, що вже впорядковані елементи (а вони будуть розташовані, починаючи з першого місця) виключаються з подальшої сортування, тому довжина кожного наступного списку (списку, який бере участь у кожному подальшому перегляді) повинна бути на один елемент менше попереднього. • Обраний мінімальний елемент, як і в попередньому випадку, переміщається на i-е місце заданого списку, а щоб це i-е місце звільнилося для запису чергового мінімального елемента, ліва від обраного елемента частину списку переміщається вправо на одну позицію так, щоб заповнилося місце, зайняте до цього вибраним елементом. Складність методу сортування вибором порядку O(n2).
Сортування вставкою та сортування злиттям
У цьому методі з невпорядкованою послідовності елементів вибирається по черзі кожен елемент, порівнюється з попереднім, вже впорядкованим, і поміщається на відповідне місце. Сортування вставкою. Таке сортування розглянемо на прикладі заданої невпорядкованою послідовності елементів: {40, 11, 83, 57, 32, 21, 75, 64}. Процедура сортування відображена на рис. 5.3, де кружком на кожному етапі обведений аналізований елемент, стрілкою зверху зазначено місце переміщення аналізованого елемента, в рамку укладені впорядковані частини послідовності. На 1-м етапі порівнюються два початкових елемента. Оскільки другий елемент менше першого, він переміщається на місце першого елемента, що зрушується вправо на одну позицію. Інша частина послідовності залишається без зміни. На 2-м етапі з невпорядкованою послідовності вибирається елемент і порівнюється з двома впорядкованими раніше елементами. Так як він більше попередніх, то залишається на місці. Потім аналізуються четвертий, п'ятий і наступні елементи до тих пір, поки весь список не буде впорядкованим, що має місце на останньому 7-м етапі.
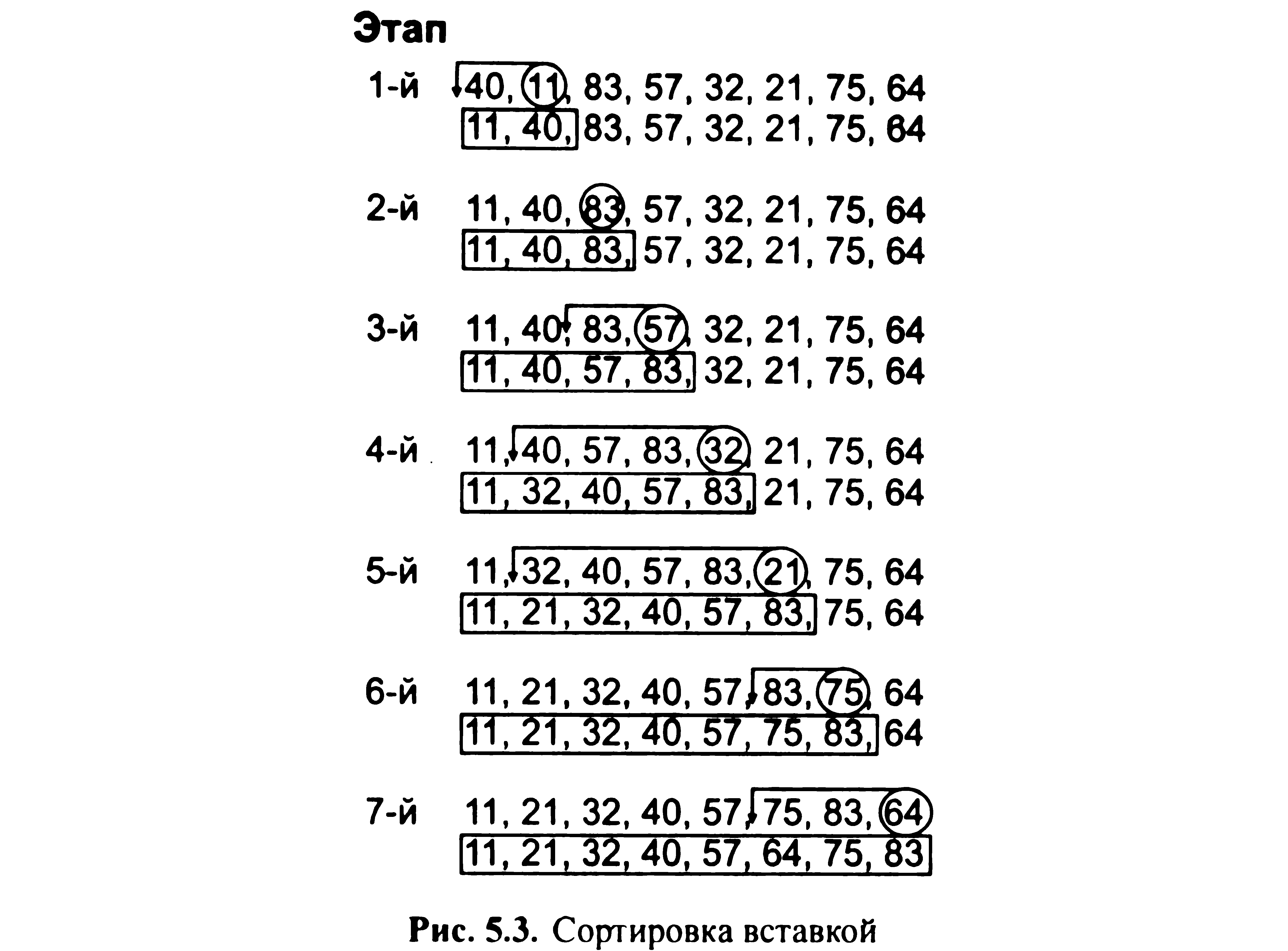
Сортировка слиянием. Разновидностью сортировки вставкой является метод фон Неймана, или сортировка слиянием. Идея метода состоит в следующем: сначала анализируются первые элементы обоих массивов. Меньший элемент переписывается в новый массив. Оставшийся элемент последовательно сравнивается с элементами из другого массива. В новый массив после каждого сравнения попадает меньший элемент. Процесс продолжается до исчерпания элементов одного из массивов. Затем остаток другого массива дописывается в новый массив. Полученный новый массив упорядочен таким же образом, как исходные.
Нехай є два відсортованих в порядку зростання масиву р[1], р[2],..., p[n] і q[2],..., q[n] і є порожній масив r[ 1], r[2],..., r[2n], який ми хочемо заповнити значеннями масивів р і q в порядку зростання. Для злиття виконуються наступні дії: порівнюються p[1] менше із значень записується в r[1]. Припустимо, що це значення р[1]. Тоді р[2] порівнюється q[1], і менше із значень заноситься до p[2]. Припустимо, що це значення. Тоді на наступному кроці порівнюються значення p[2] і q[2] і т.д., поки ми не досягнемо кордонів одного з масивів. Тоді залишок іншого масиву просто дописується в «хвіст» масиву r. Приклад злиття двох масивів показаний на рис. 5.4. Складність методу сортування вставкою порядку O(п2).
Сортування обміном та шейкерне сортування
Сортування обміном. Це метод, в якому елементи списку послідовно порівнюються між собою і міняються місцями в тому випадку, якщо попередній елемент більше подальшого. Потрібно, наприклад, провести сортування списку методом стандартного обміну, або методом «бульбашки»: {40, 11, 83, 57, 32, 21, 75, 64}. Позначимо квадратними дужками зі стрілками обмінювані елементи, а |__| - порівнювані елементи. Перший етап сортування показаний на рис. 5.5, а другий етап - на рис. 5.6. Неважко бачити, що після кожного перегляду списку всі елементи, починаючи з останнього, займають свої остаточні позиції, тому їх не слід перевіряти при наступних переглядах. Кожен подальший перегляд виключає чергову позицію зі знайденим максимальним елементом, тим самим скорочуючи список. Після першого перегляду в останній позиції опинився більший елемент, рівний 83 (виключаємо його з подальшого розгляду). Другий перегляд виявляє максимальний елемент, що дорівнює 75 (див. мал. 5.6). Процес сортування продовжується до тих пір, поки не будуть сформовані всі елементи кінцевого списку або не виконується умова Айверсона. Умова Айверсона: якщо в ході сортування при порівнянні елементів не було зроблено жодної перестановки, то безліч вважається впорядкованим (умова Айверсона виконується тільки при кроці d= 1).
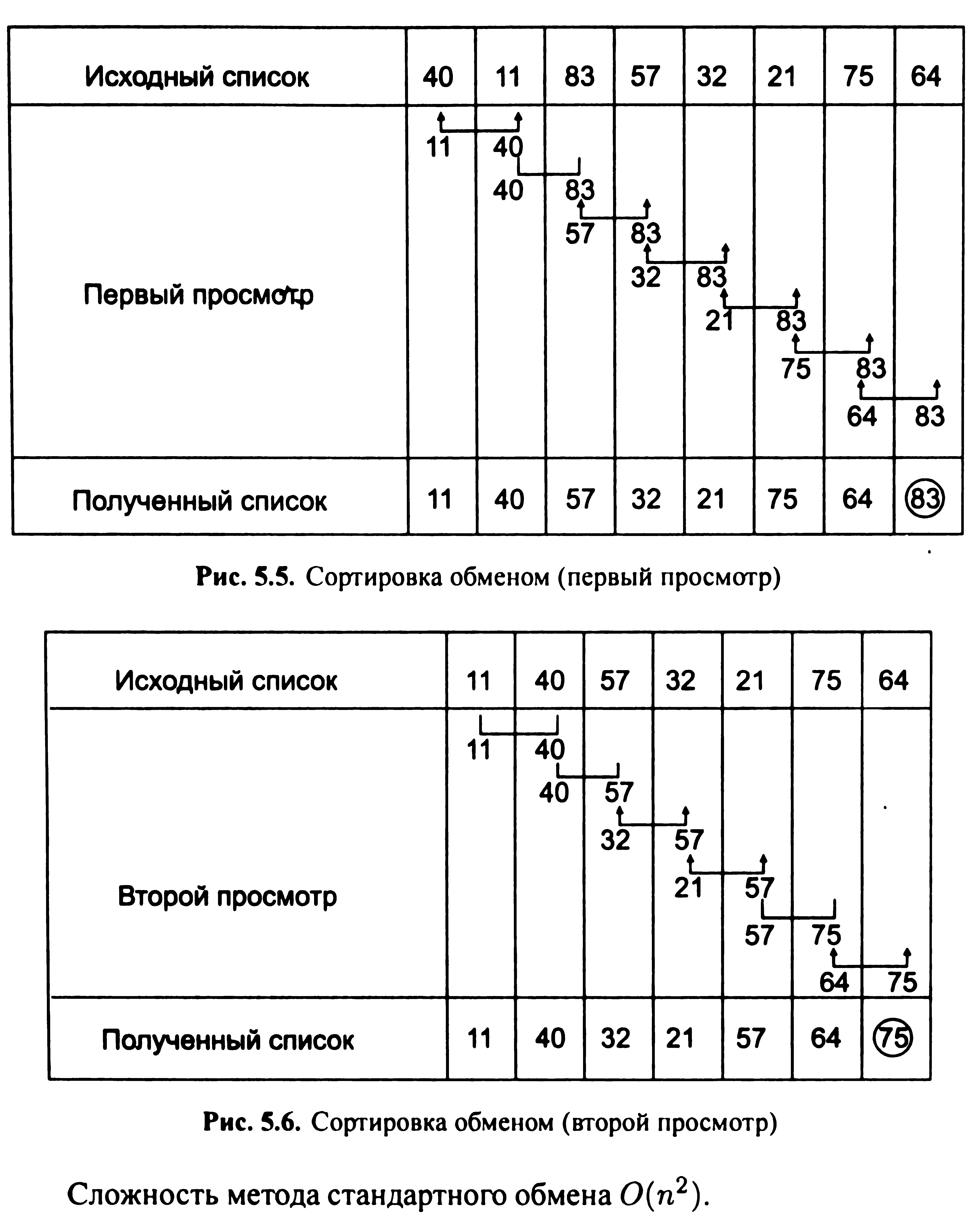
Шейкерне сортування. Очевидний прийом поліпшення алгоритму стандартного обміну - запам'ятовувати, були чи не були перестановки в процесі деякого проходу. Якщо в останньому проході перестановок не було, то алгоритм можна закінчувати. Це поліпшення, однак, можна знову ж поліпшити, якщо запам'ятовувати не тільки сам факт, що обмін мав місце, але і положення (індекс) останнього обміну. Ясно, що всі пари сусідніх елементів вище цього індексу k
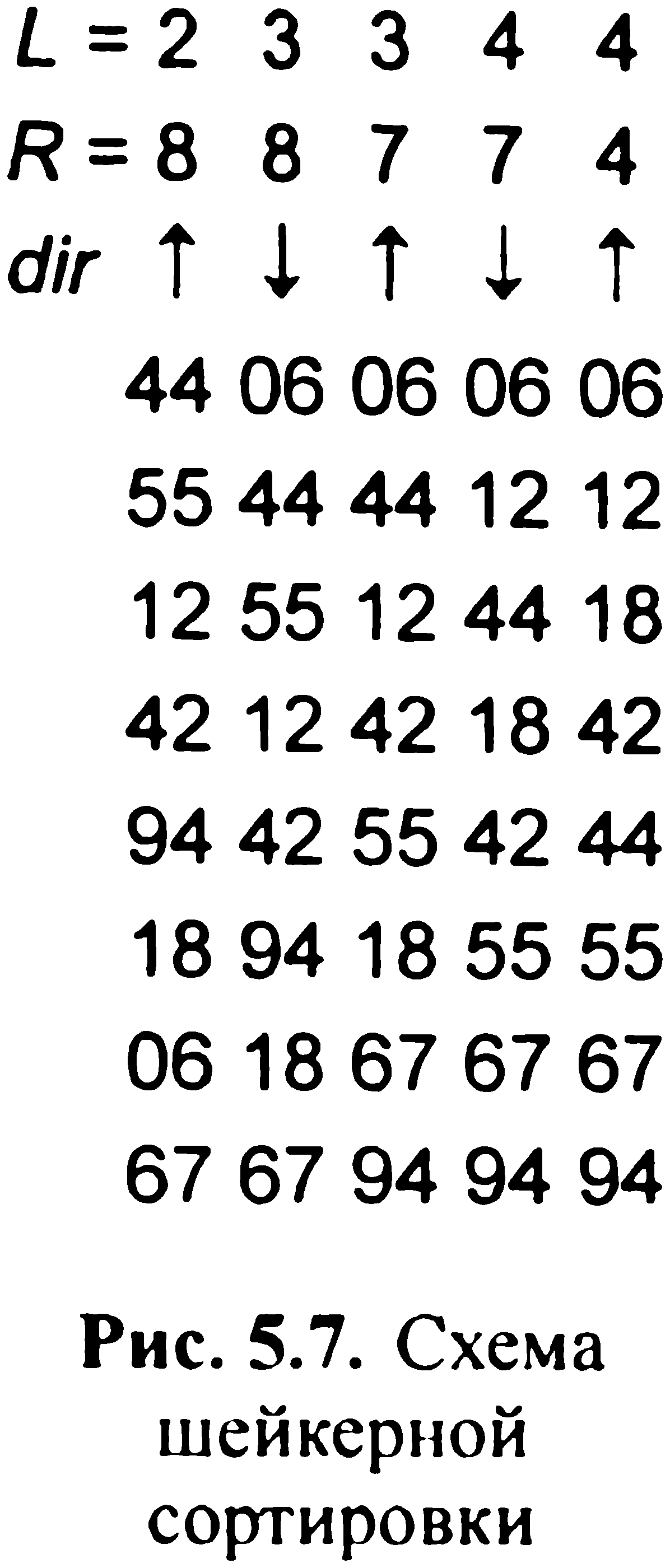
вже впорядковані. Тому перегляди можна закінчувати на цьому індексі, а не йти до заздалегідь визначеного нижньої межі для р. Наприклад, масив{12, 18, 42, 44, 55, 67, 94, 06} за допомогою вдосконаленої «бульбашкової» сортування можна впорядкувати за один перегляд, а для сортування масиву{94, 06, 12, 18, 42, 44, 55, 67} потрібно сім переглядів. Це призводить до думки: чергувати напрямок послідовних переглядів. Модифікацією сортування стандартним обміном є шейкерная, або човникова, сортування. На рис. 5.7 наведена схема шейкерного сортування восьми ключів.
Сортування Шелла
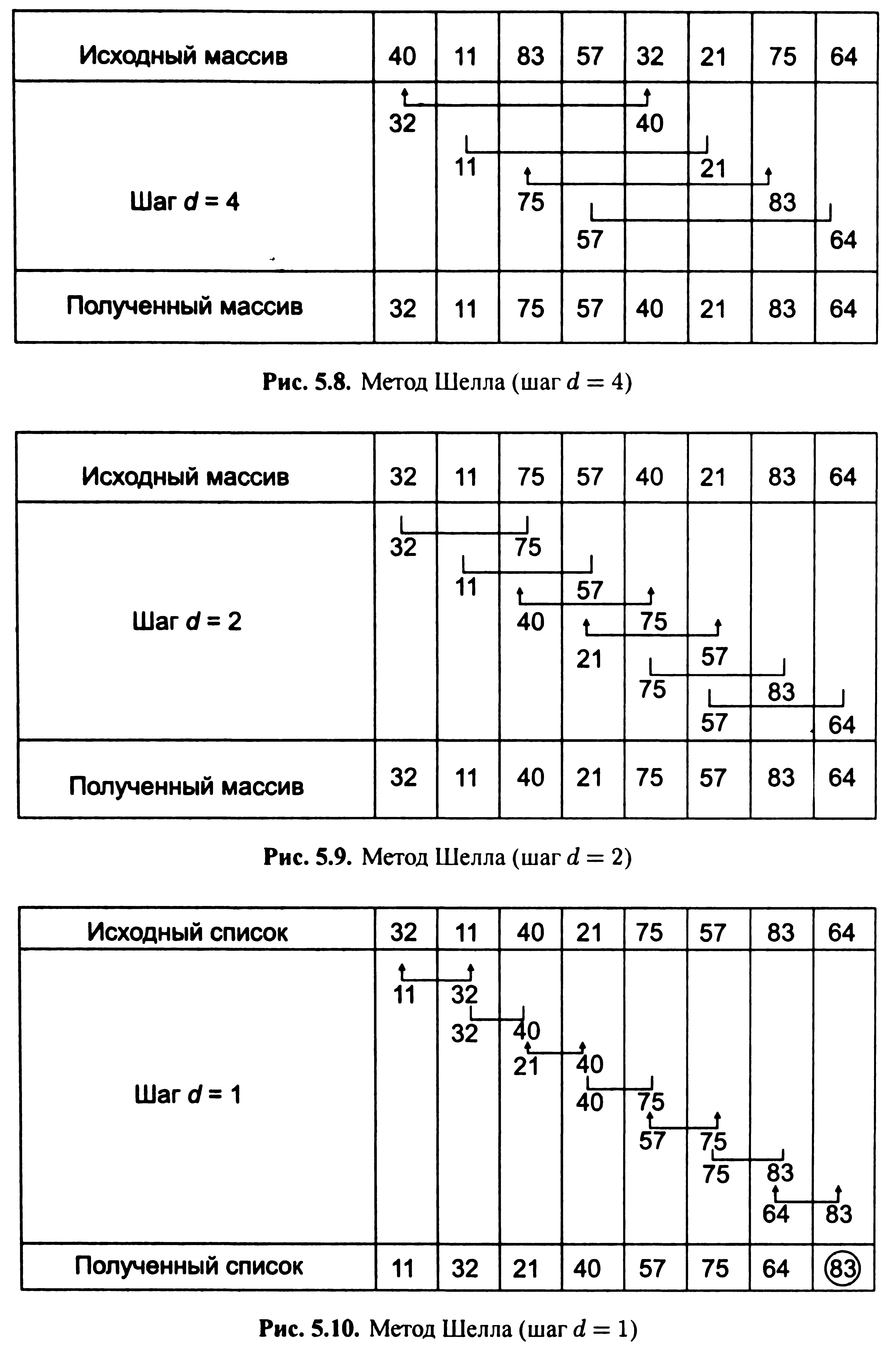
У методі Користувача порівнюються не сусідні елементи, а елементи, розташовані на відстані d(де d - крок між сравниваемыми елементами). Якщо d- [n/2], то після кожного перегляду крок d, зменшується вдвічі. На останньому перегляді він скорочується до d - 1. Наприклад, нехай дано список, у якому кількість елементів парне: {40, 11, 83, 57, 32, 21, 75, 64}. Список довжини п розбивається на n/2 частин, тобто d = [n/2] = 4, де [ ] - ціла частина числа. При першому перегляді порівнюються елементи, віддалені один від одного на d = 4 (мал. 5.8), тобто k1 і k5, k2 і k6 і т.д. Якщо ki > ki+d, то відбувається обмін між позиціями i (i + d). Перед другим переглядом вибирається крок d = [d/2] = 2 (рис. 5.9). Потім вибираємо крок d= [d/2] = 1 (рис. 5.10), тобто маємо аналогію з методом стандартного обміну.
![]()
Швидке сортування (сортування Хоара)
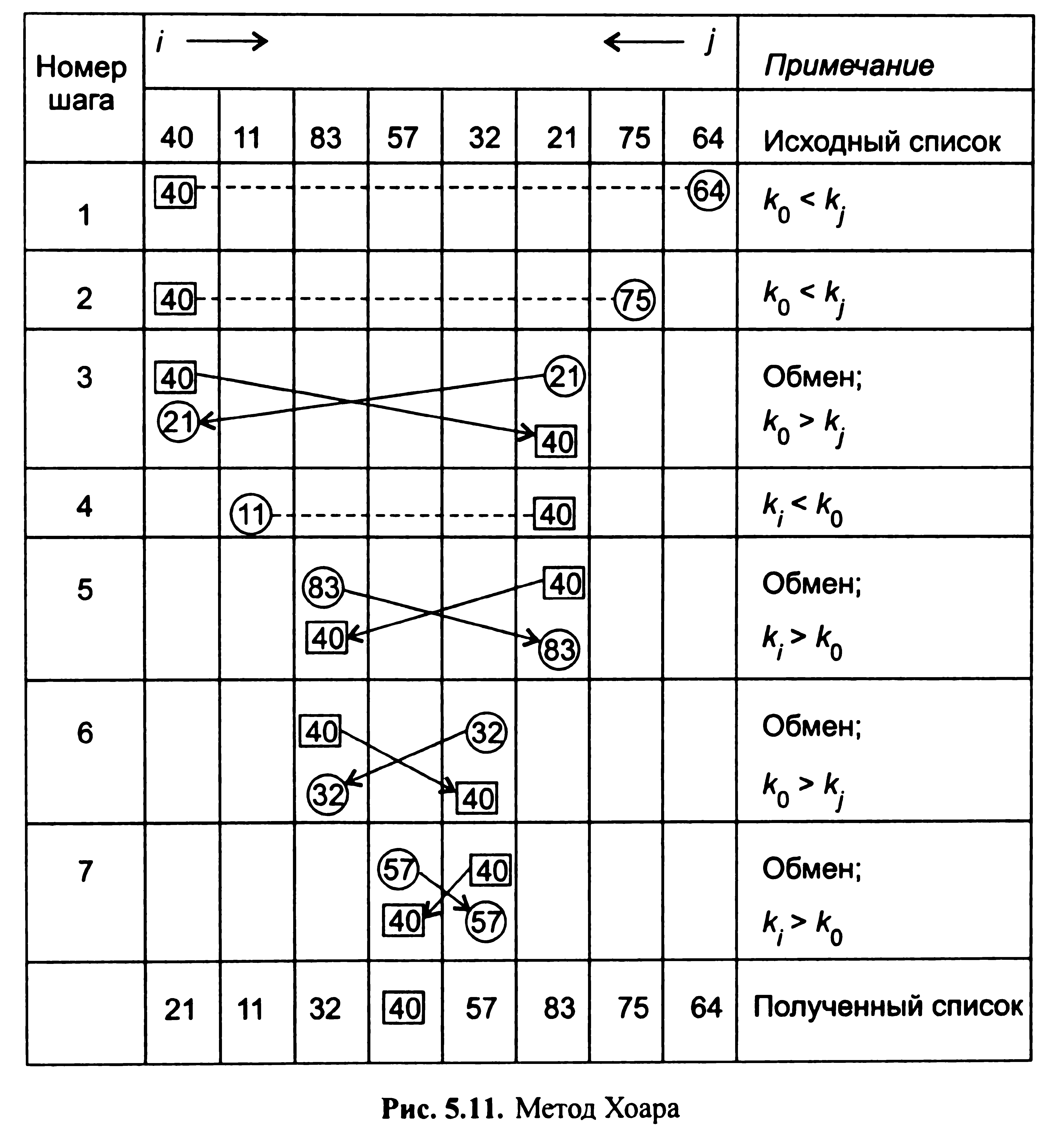
У методі швидкого сортування фіксується якийсь ключ (базовий), щодо якого всі елементи з великою вагою переміщуються вправо, а з меншим - ліворуч. При цьому весь список елементів ділиться щодо базового ключа на дві частини. Для кожної частини процес повторюється. Пояснимо метод на прикладі. На рис. 5.11 представлені етапи швидкого сортування Хоара. У першому рядку вказана вихідна послідовність.

Турнірне сортування
Елементи
вихідного безлічі представляються
листям дерева. Їх попарное порівняння
дозволяє визначити мінімальний
(максимальний) елемент. Метод турнірній
сортування заснований на повторюваних
пошуках найменшого ключа серед п
елементів, серед решти п - 1 елементів і
т.д. Наприклад, зробивши n/2 порівнянь,
можна визначити в кожній парі ключів
менший. За допомогою n/4 порівнянь - менший
з пари вже обраних менших і т.д.
Проробивши
n - 1 порівнянь, можна побудувати дерево
вибору (мал. 5.12) і ідентифікувати його
корінь як найменший ключ.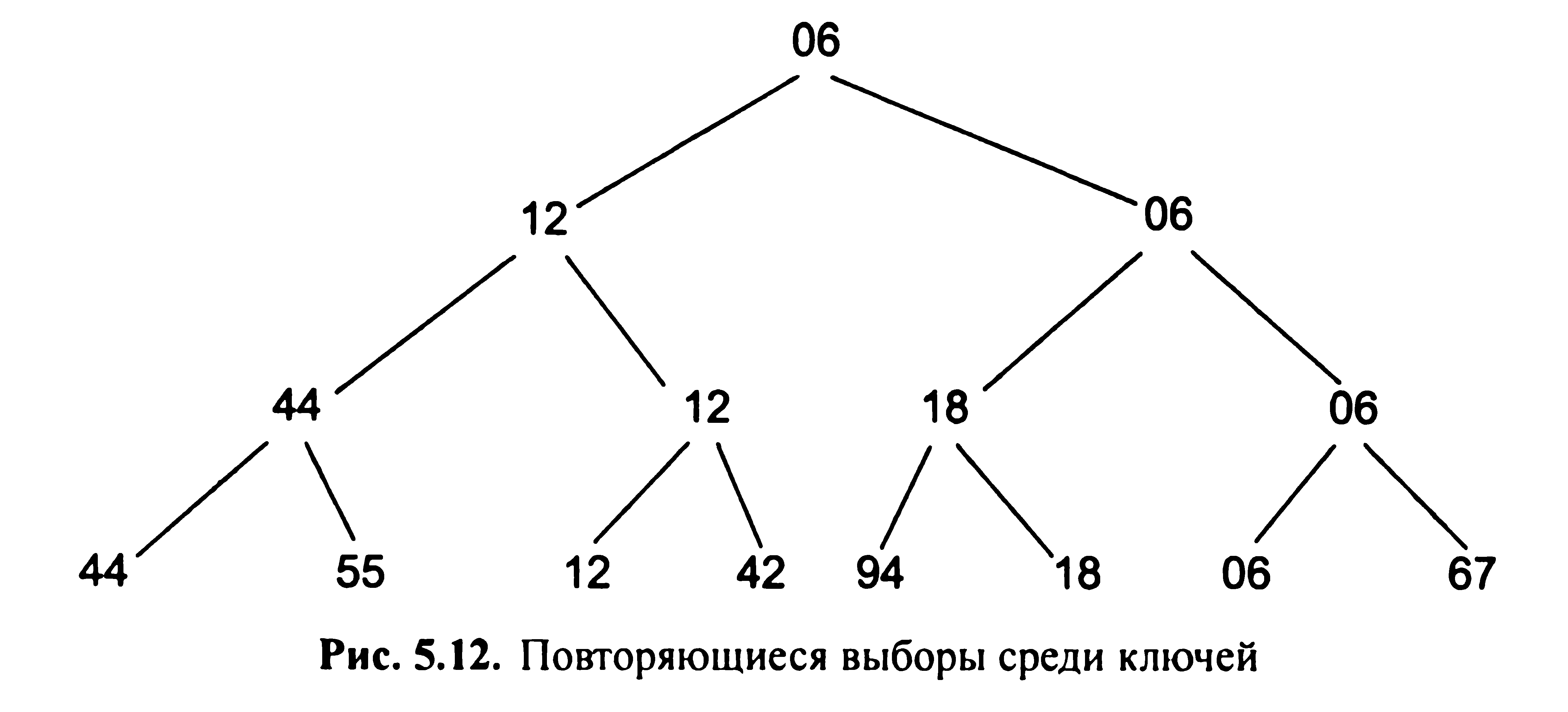
Следующий этап сортировки — спуск вдоль пути, отмеченного наименьшим элементом, и исключение его из дерева путем замены либо на пустой элемент (дырку) в самом низу, либо на элемент из соседней ветви в промежуточных вершинах (рис. 5.13).
Рис.
5.13. Исключение наименьшего ключа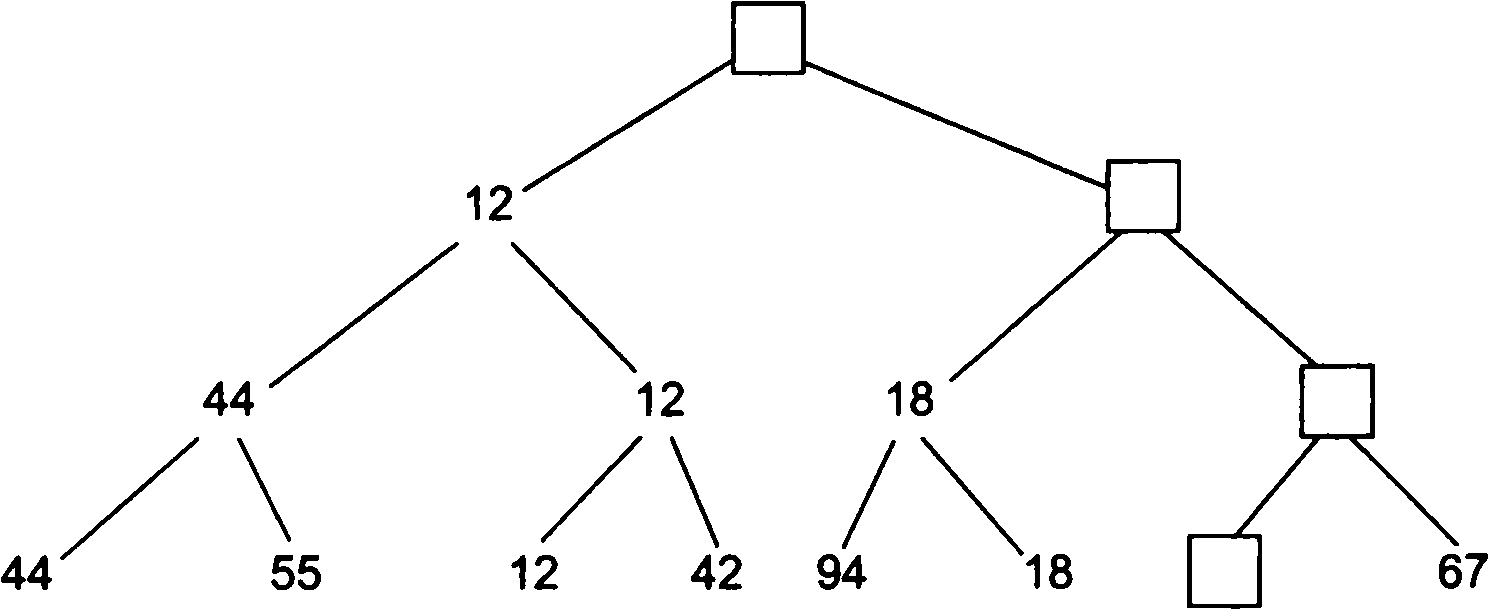
Е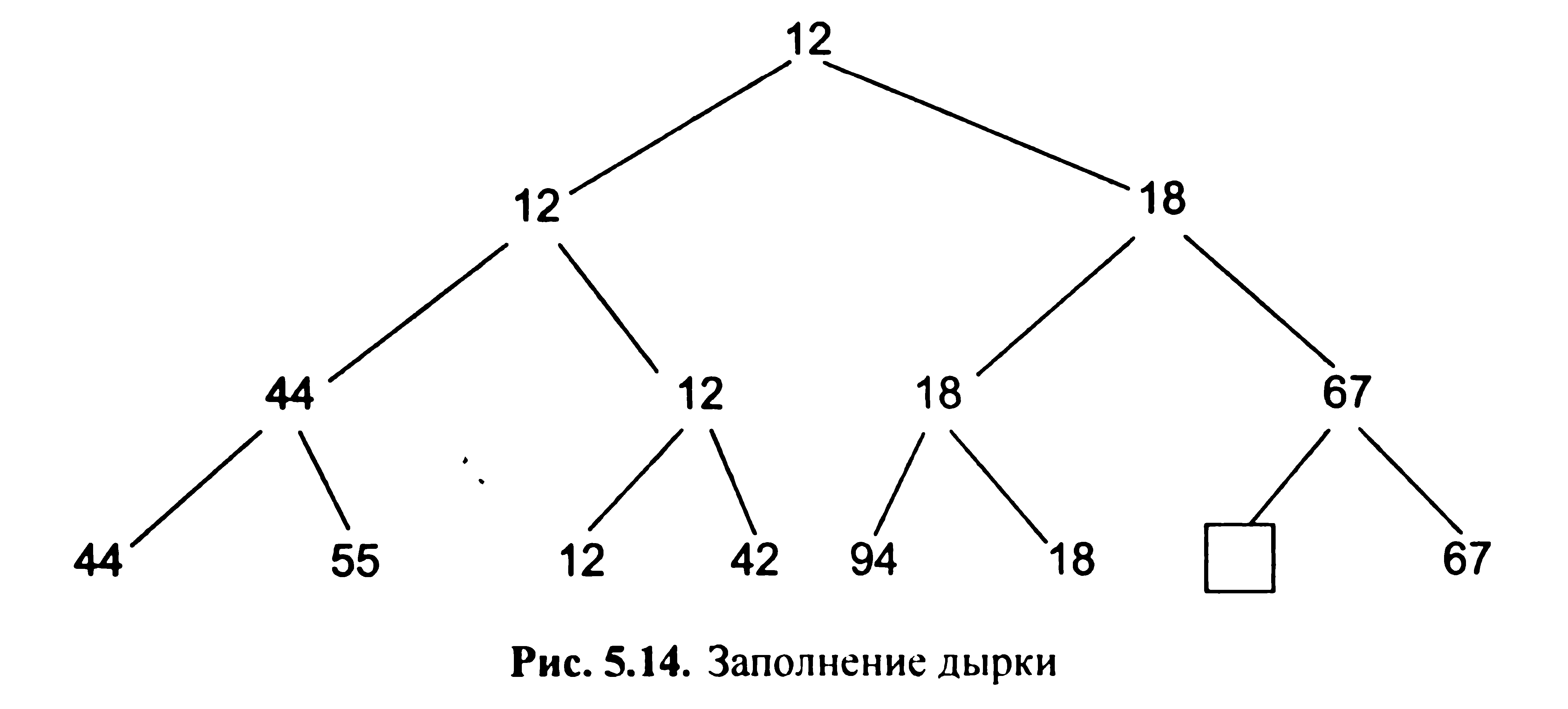 лемент,
передвинувшийся в корінь дерева, знову
буде найменшим (тепер вже другим ключем
(мал. 5.14), і його можна виключити. Після
п таких кроків дерево стане порожнім
(тобто в ньому залишаться одні дірки),
і процес сортування закінчується.
Свою
назву турнірна сортування отримала,
тому що вона використовується при
проведенні змагань, турнірів і
олімпіад.
Приклад
1. Дано вихідне безліч {а1, а2, а3, а4, а5, а6,
а7, а8}. Здійснити турнірну сортування.
лемент,
передвинувшийся в корінь дерева, знову
буде найменшим (тепер вже другим ключем
(мал. 5.14), і його можна виключити. Після
п таких кроків дерево стане порожнім
(тобто в ньому залишаться одні дірки),
і процес сортування закінчується.
Свою
назву турнірна сортування отримала,
тому що вона використовується при
проведенні змагань, турнірів і
олімпіад.
Приклад
1. Дано вихідне безліч {а1, а2, а3, а4, а5, а6,
а7, а8}. Здійснити турнірну сортування.
П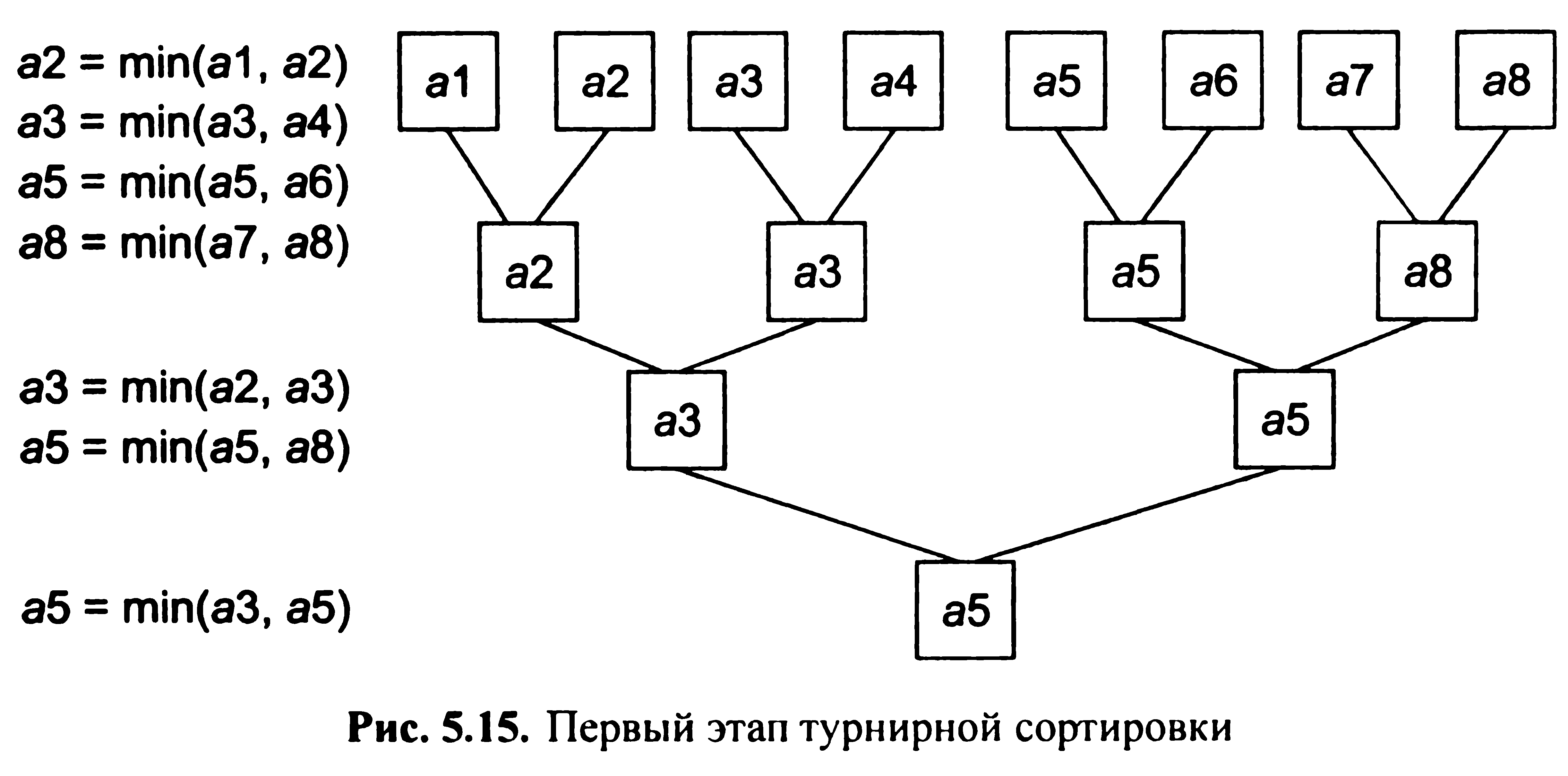 роводиться
попарное порівняння вершин дерева (мал.
5.15). Знайдений мінімальний елемент
замінюється спеціальним символом М і
поміщається в результуюче безліч (мал.
5.16).
роводиться
попарное порівняння вершин дерева (мал.
5.15). Знайдений мінімальний елемент
замінюється спеціальним символом М і
поміщається в результуюче безліч (мал.
5.16).
На наступних етапах знайдені мінімальні елементи поміщаються в результуюче безліч (мал. 5.17).
Пирамідальне сортування
Даний тип сортування полягає в побудова пірамідального дерева. Пірамідальне дерево - це бінарне дерево, володіє трьома властивостями:
у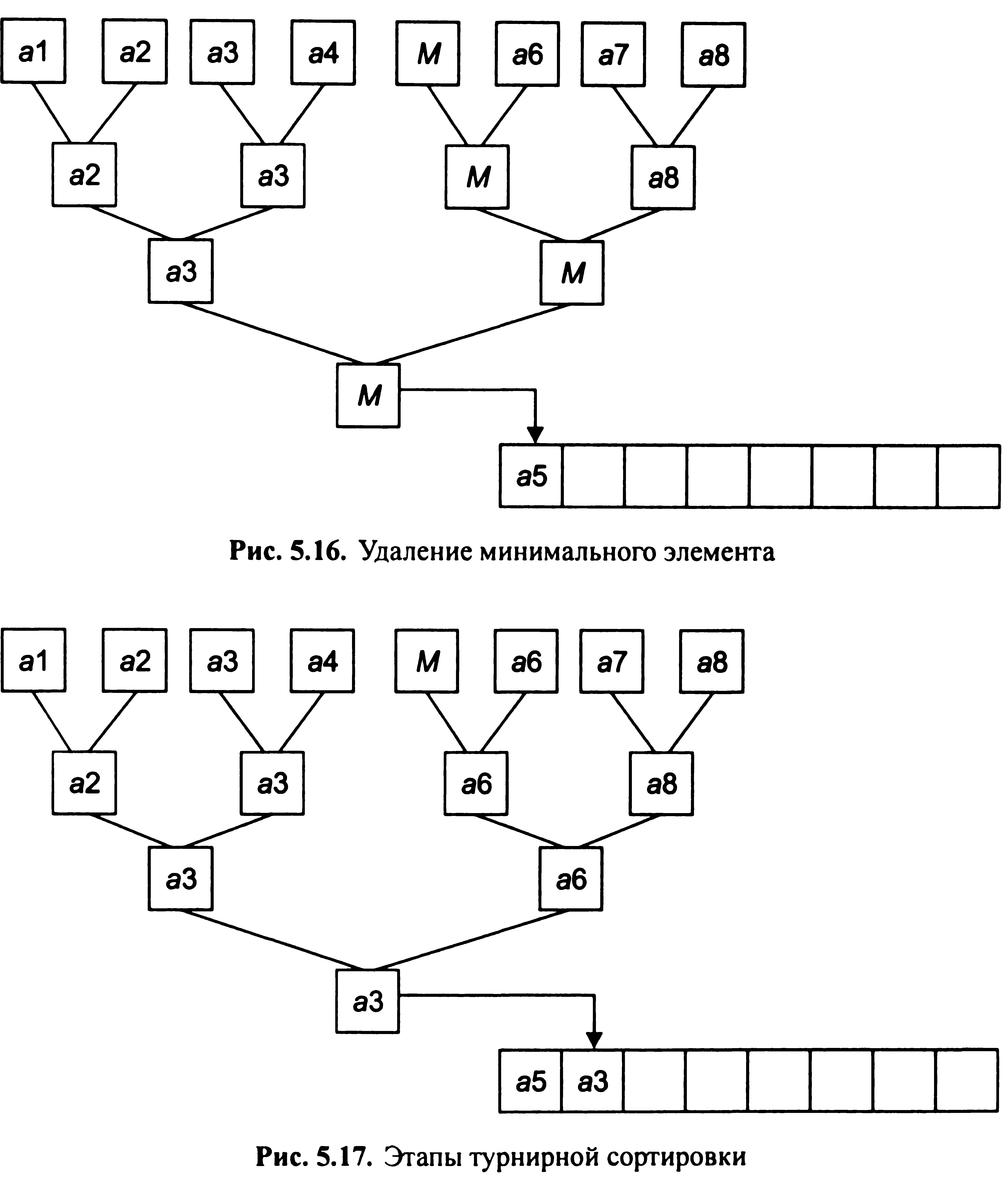 вершині кожної тріади розташовується
елемент з великою вагою;
•
листя бінарного дерева розташовуються
або в одному рівні, або у двох сусідніх
(мал. 5.18);
•
листя нижнього рівня розташовуються
лівіше листя більш високого рівня.
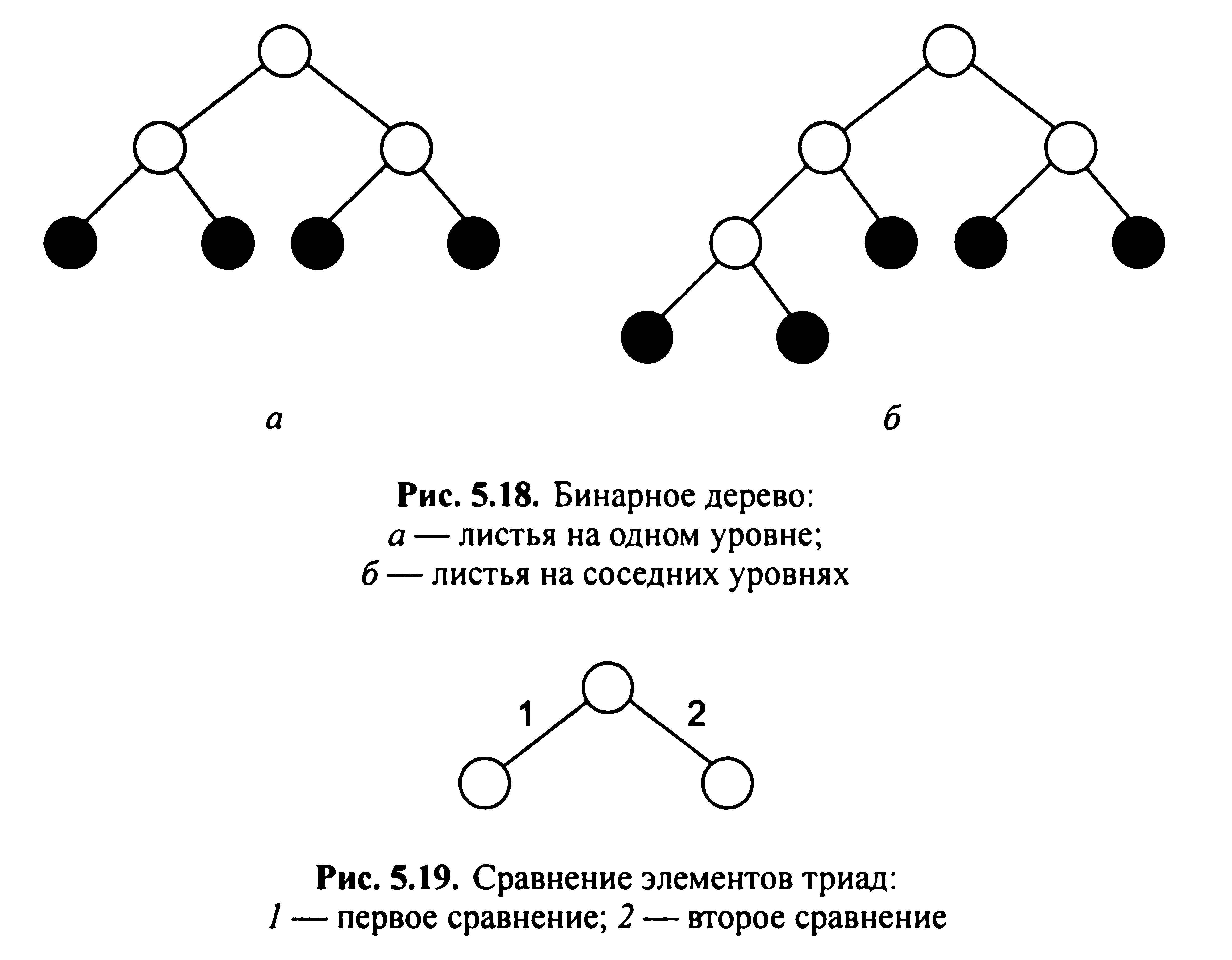
В
ході перетворення елементи тріад
порівнюються двічі (мал. 5.19), при цьому
елемент з великою вагою перейде вгору,
а з меншим - вниз.
вершині кожної тріади розташовується
елемент з великою вагою;
•
листя бінарного дерева розташовуються
або в одному рівні, або у двох сусідніх
(мал. 5.18);
•
листя нижнього рівня розташовуються
лівіше листя більш високого рівня.
В
ході перетворення елементи тріад
порівнюються двічі (мал. 5.19), при цьому
елемент з великою вагою перейде вгору,
а з меншим - вниз.
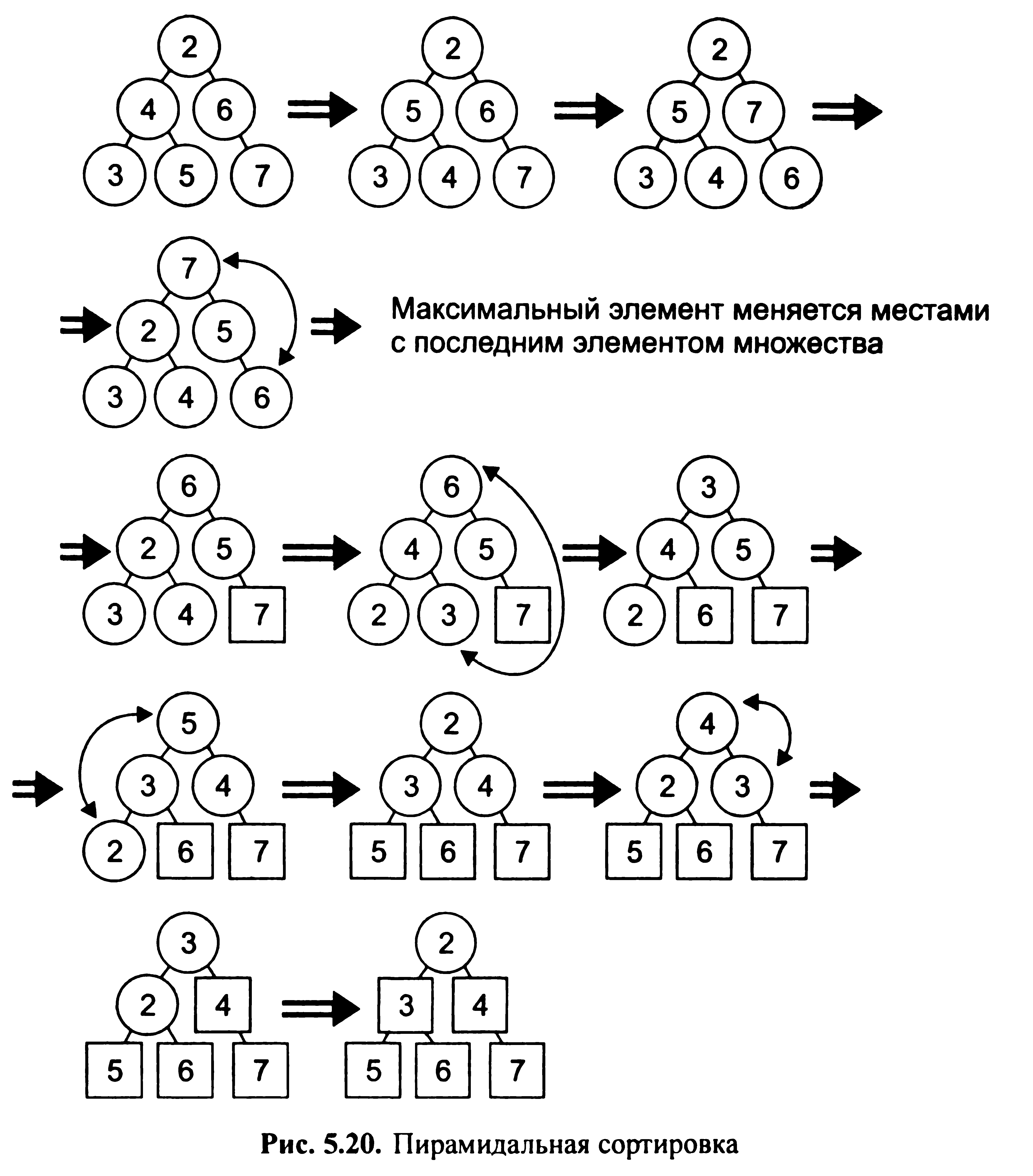
Приклад. Дано вихідне безліч{2, 4, 6, 3, 5, 7}. В ході сортування послідовно порівнюються елементи тріад. При цьому елемент з великою вагою переміщається в корінь дерева. Після завершення етапу сортування елемент, що перебуває в корені дерева, поміщається на місце останнього елемента і надалі не розглядається. Метод пірамідальної сортування показаний на рис. 5.20. В результаті буде отримано впорядкована множина{2, 3, 4, 5, 6, 7}.
Контрольні питання 1. Що розуміється під сортуванням? 2. Які особливості сортування: вставкою, вибором, обміном? 3. Які особливості сортування Користувача і Хоара? 4. Які особливості сортування турнірній і пірамідальної? 5. Яка основна ідея шейкерной сортування? 6. До якої групи методів належить сортування фон Неймана? 7. У чому полягає методика аналізу складності алгоритмів сортування?
Методи пошуку
Предмети (об'єкти), що становлять безліч, називаються його елементами. Елемент безлічі буде називатися ключем і позначатися латинською літерою k1 з індексом, вказує номер елемента. Алгоритми пошуку можна розбити на наступні групи (мал. 6.1).
Рис.
6.1. Методы поиска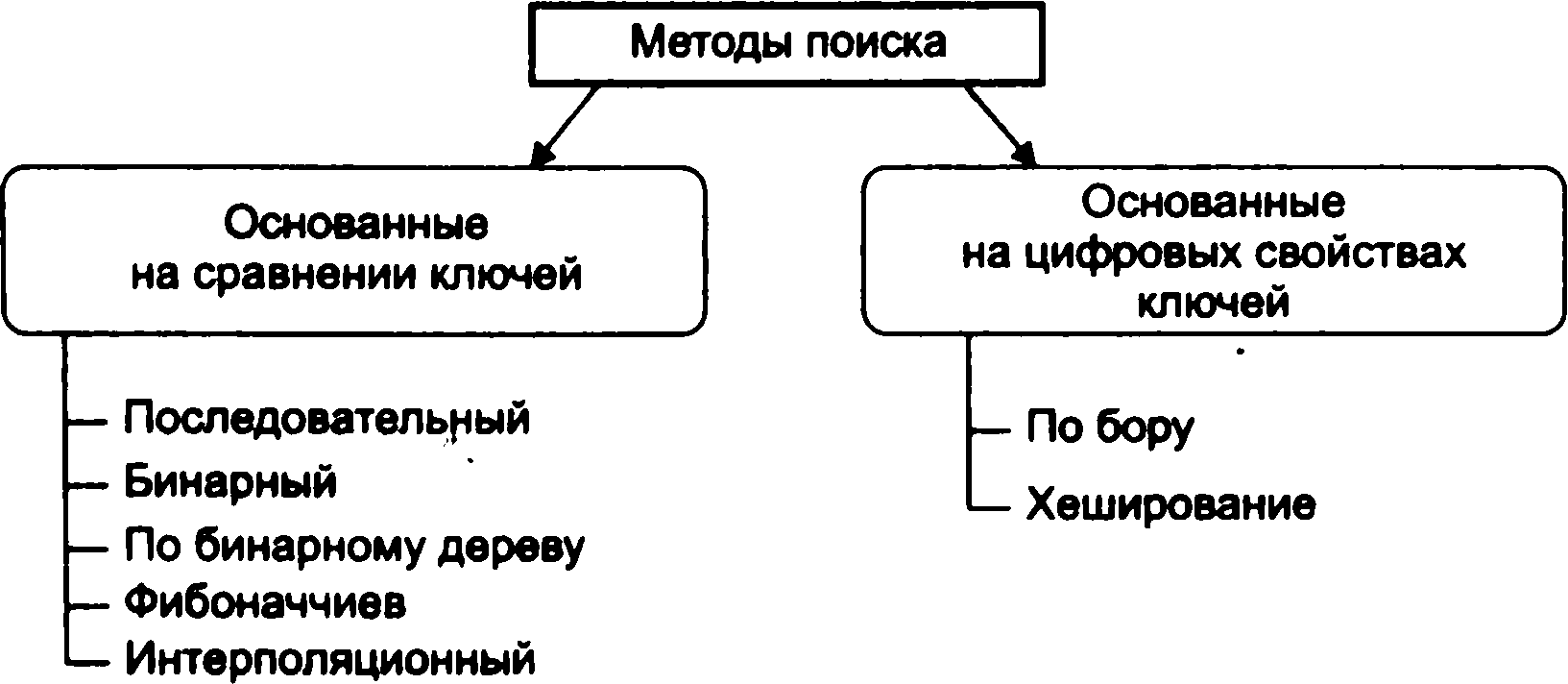
Задача пошуку. Нехай задано множину ключів (k1,k2,k3,...,kn). Необхідно відшукати в безлічі ключ ki. Пошук може бути завершений у двох випадках: • ключ у безлічі відсутня; • ключ знайдений у множині.
Послідовний пошук
У послідовному пошуку вихідне безліч не впорядковано, тобто є довільний набір ключів {Агх, А:з, кп}. Метод полягає в тому, що відшукуваний ключ кх послідовно порівнюється з усіма елементами множини. При цьому пошук закінчується достроково, якщо ключ знайдений. Алгоритм пошуку зводиться до послідовності кроків: Крок S1. [Початкова установка.] Встановити i := 1. Крок S2. [Порівняння.] Якщо k=ki, алгоритм закінчується вдало. Крок S3. [Просування.] Збільшити i на 1. Крок S4. [Кінець файлу?] Якщо i ≤ N. то повернутися до кроку S2. В іншому випадку алгоритм закінчується невдало.
Бінарний пошук
У
бінарному пошуку вихідне безліч повинно
бути впорядковано за зростанням, іншими
словами, кожний наступний ключ більше
попереднього, тобто k1≤ k2≤k3 ≤k4 ≤ ... ≤
kn-1≤ кп.
Відшукуваний
ключ порівнюється з центральним елементом
множини, якщо він менше центрального,
то пошук триває в лівому підмножині, в
іншому випадку - в правому.
Медіаною
послідовності з п елементів вважається
елемент, значення якого менше або
дорівнює) половини п елементів і більше
(або дорівнює) іншої половини. Завдання
пошуку медіани прийнято пов'язувати з
сортуванням, так як медіану завжди можна
знайти наступним способом: відсортувати
п елементів і потім вибрати середній
елемент.
В
алгоритмі. Хоара для знаходження медіани
використовується операція поділу, що
застосовується при швидкій сортування,
з L = 1, R = п а д[k], обраними як поділ значення
х. Виходять значення індексів i j.
1)
розділяє значення х було занадто мало,
в результаті кордон між двома частинами
нижче шуканого значення k. Процес поділу
слід повторити для е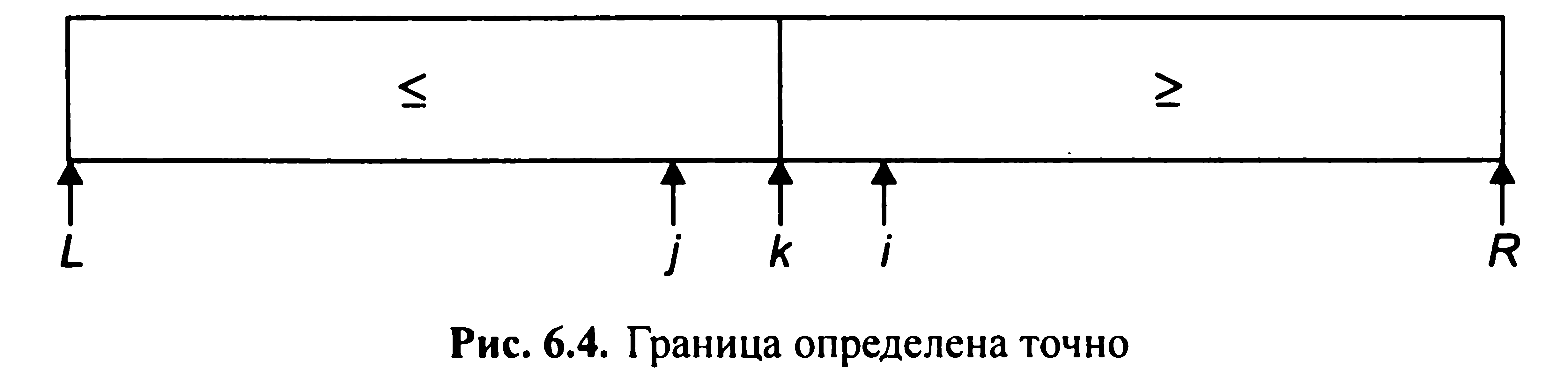 лементів
а[i],..., а[R] (рис. 6.2);
лементів
а[i],..., а[R] (рис. 6.2);
3) значення k лежить в інтервалі j < k < i: елемент а[k] розділяє масив в заданій пропорції і, отже, є шуканим (мал. 6.4). Процес розподілу повторюється до появи останнього випадку. Центральний елемент знаходиться за формулою Nэл-та = [n/2] + 1, де квадратні дужки означають, що від ділення береться тільки ціла частина, дробова частина відкидається. У методі бінарного пошуку аналізуються тільки центральні елементи підмножин. Приклад 1. У безлічі елементів відшукати ключ, рівний 653. У квадратних дужках виділені безлічі аналізованих елементів. Центральні елементи підмножин підкреслені. Пошук ключа До = 653 здійснюється за чотири кроки:
П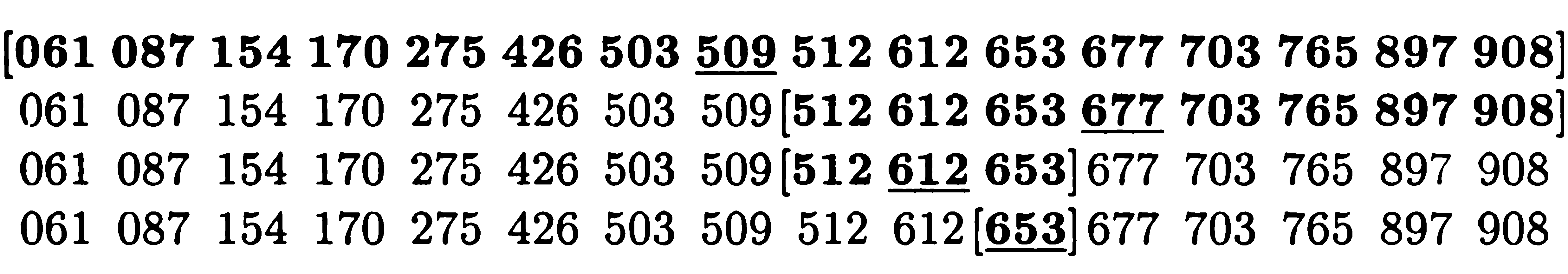 риклад
2. Дано впорядкована множина елементів{7,
8, 12, 16, 18, 20, 30, 38, 49, 50, 54, 60, 61, 69,75, 79, 80, 81,
95,101, 123, 198}.
Знайти
в множині
ключ =61.
риклад
2. Дано впорядкована множина елементів{7,
8, 12, 16, 18, 20, 30, 38, 49, 50, 54, 60, 61, 69,75, 79, 80, 81,
95,101, 123, 198}.
Знайти
в множині
ключ =61.


Фібоначчиєв пошук
У цьому пошуку аналізуються елементи, що знаходяться в позиціях, рівних чисел Фібоначчі. Числа Фібоначчі виходять за наступним правилом: кожне наступне число дорівнює сумі двох попередніх чисел, наприклад: {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...}. Пошук продовжується до тих пір, поки не буде знайдено інтервал між двома ключами, де може розташовуватися відшукуваний ключ. Фибоначчиев пошук призначається для пошуку аргументу До серед розташованих у порядку зростання ключів К1 < К2 < ...<Кп. Для зручності описания передбачається, що п + 1 є число Фібоначчі Підходящої початкової установкою даний метод можна зробити придатним для будь-якого п. F1. [Початкова установка.] Встановити i:=Fk, p:=Fk-1, q:=Fk-2 (В алгоритмі р і q позначають послідовні числа Фібоначчі.) F2. [Порівняння.] Якщо До < Кі, то перейти на якщо До >Ki то перейти на F4; якщо До = Ki, алгоритм закінчується вдало.

Інтерполяційний пошук
В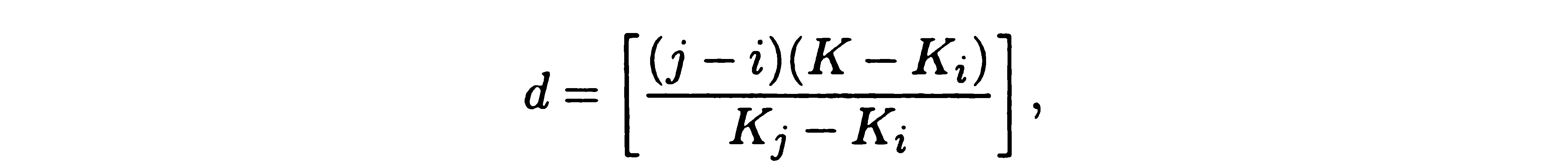 ихідна
множина
повинна
бути впорядкована
за зростанням ваги.
Первинне порівняння здійснюється на
відстані кроку (I, який визначається за
формулою:
ихідна
множина
повинна
бути впорядкована
за зростанням ваги.
Первинне порівняння здійснюється на
відстані кроку (I, який визначається за
формулою:

І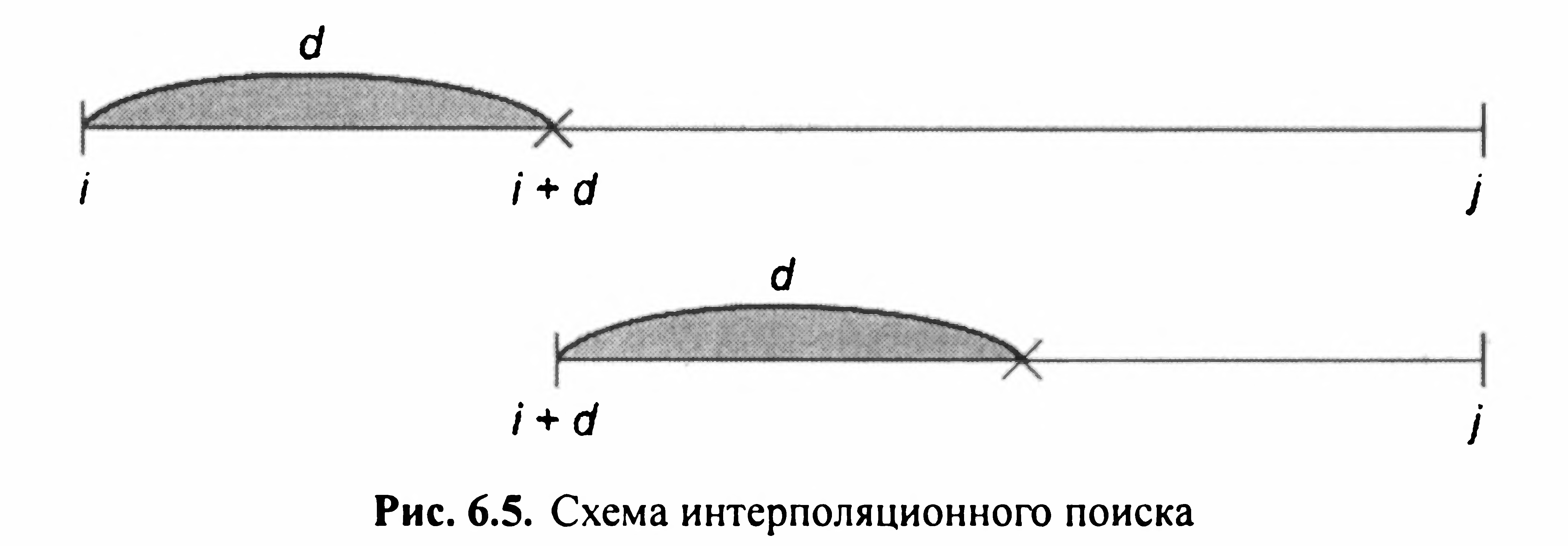 дея
методу полягає в наступному: крок d
змінюється після кожного етапу за
формулою, наведеною вище (мал. 6.5).
дея
методу полягає в наступному: крок d
змінюється після кожного етапу за
формулою, наведеною вище (мал. 6.5).
Алгоритм закінчує роботу при (d = 0, при цьому аналізуються сусідні елементи, після чого приймається остаточне рішення про результати пошуку. Цей метод працює чудово, якщо вихідне безліч являє собою арифметичну прогресію або безліч, наближене до неї. Приклад 1. Дано багато ключів: {2, 9, 10, 12, 20, 24, 28, 30, 37, 40, 45, 50, 51, 60, 65, 70, 74, 76}. Нехай потрібний ключ = 70.
Порівнюємо
ключ, стоящий під шістнадцятим порядковим
номером у даному безлічі з шуканим
ключем: k16
V;
70 = 70; ключ знайдений.
Приклад
2. Дано багато ключів: {4, 5, 10, 23, 24, 30, 47,
50, 59, 60, 64, 65, 77, 90, 95, 98, 102}. Потрібно відшукати
ключ = 90.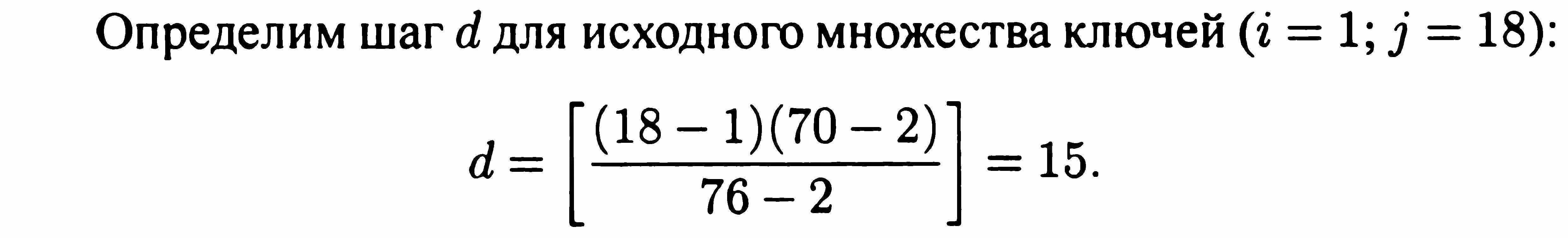

Пошук по бінарному дереву
Дерево
двійкового пошуку для безлічі чисел S
- це розмічене бінарне дерево, кожній
вершині якого зіставлений число з
безлічі S,
причому всі позначки задовольняють
наступного простого правила: «якщо
більше - праворуч, якщо менше -
ліворуч».
Наприклад,
для набору номерів{7, 3, 5, 2, 8, 1, 6, 10, 9, 4,
11} вийде бінарне дерево (мал. 6.6). Для
того щоб правильно врахувати повторення
чисел, можна ввести додаткове поле, яке
буде зберігати кількість записів для
кожного числа.
Бінарне
дерево, відповідне бінарним пошуку
серед га записів, можна побудувати
наступним чином: при n = 0 дерево зводиться
до вузла 0. В іншому випадку кореневим
вузлом є [n/2], ліве піддерево відповідає
бінарним дереву з [n/2] -1 вузлами, а праве
- дереву з [n/2] вузлами і числами у вузлах,
збільшеними на [n/2] (рис. 6.7).
К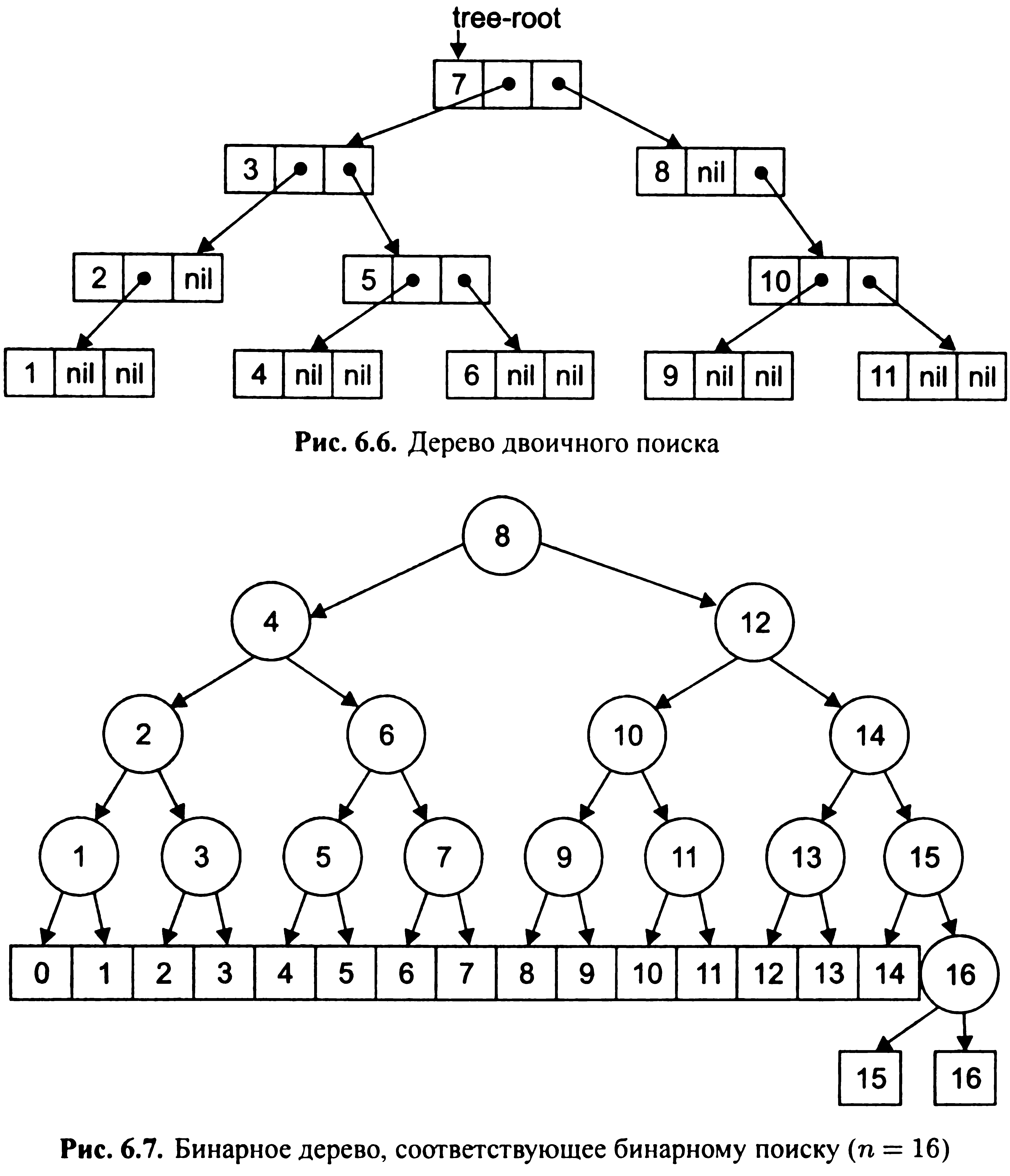 ількість
вузлів, породжених окремим вузлом
(число піддерев даного кореня), називається
його ступенем. Вузол з нульовим ступенем
ількість
вузлів, породжених окремим вузлом
(число піддерев даного кореня), називається
його ступенем. Вузол з нульовим ступенем
називають листом, або кінцевим вузлом. Максимальне значення ступеня всіх вузлів даного дерева називається ступенем дерева. Алгоритм пошуку по бінарним дереву: спочатку аргумент пошуку порівнюється з ключем, що в корені. Якщо аргумент збігається з ключем, пошук завершено, якщо не збігається, то в разі, коли аргумент виявляється менше ключа, пошук триває в лівому поддереве, а у разі, коли більше ключа, - у правому поддереве. Збільшивши рівень на 1, повторюють порівняння, вважаючи поточний вузол коренем. Використання структури бінарного дерева дозволяє швидко вставляти і видаляти записи і проводити ефективний пошук по таблиці. Така гнучкість досягається додаванням у кожну запис двох полів для зберігання посилань. Нехай дано бінарне дерево пошуку (мал. 6.8). Потрібно бінарним дереву відшукати ключ SАG.
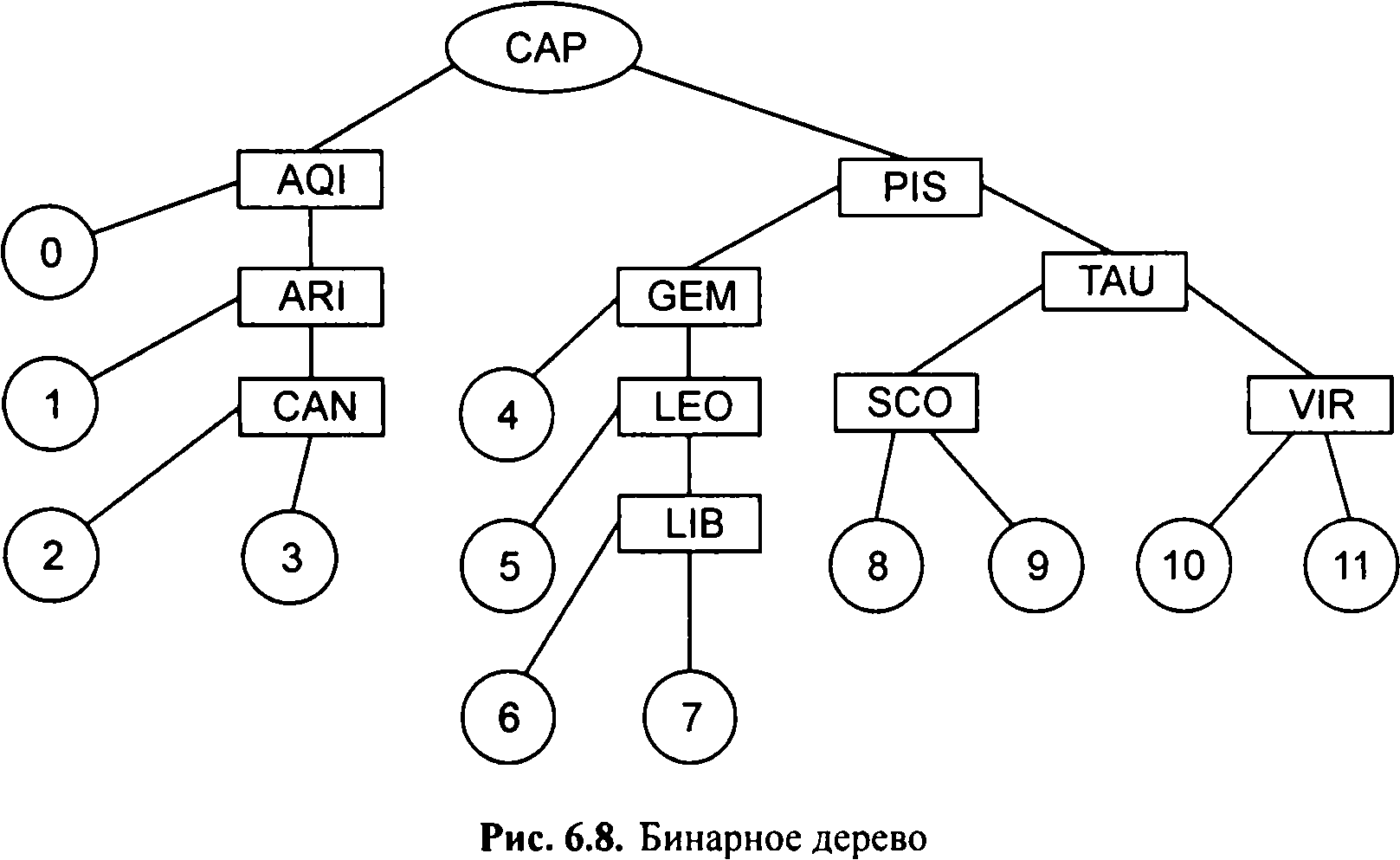
При перегляді від кореня дерева видно, що з першої букви латинського алфавіту назва GАG більше ніж САР. Отже, подальший пошук будемо здійснювати в правій гілки. Це слово більше, ніж Р1S, значить, знову йдемо вправо; воно менше, ніж ТАU, - йдемо вліво; воно менше, ніж SСО, потрапляємо в вузол 8. Таким чином, назва SАG повинно знаходитися у вузлі 8. При цьому вузли дерева мають структуру, представлену в табл. 6.1.

П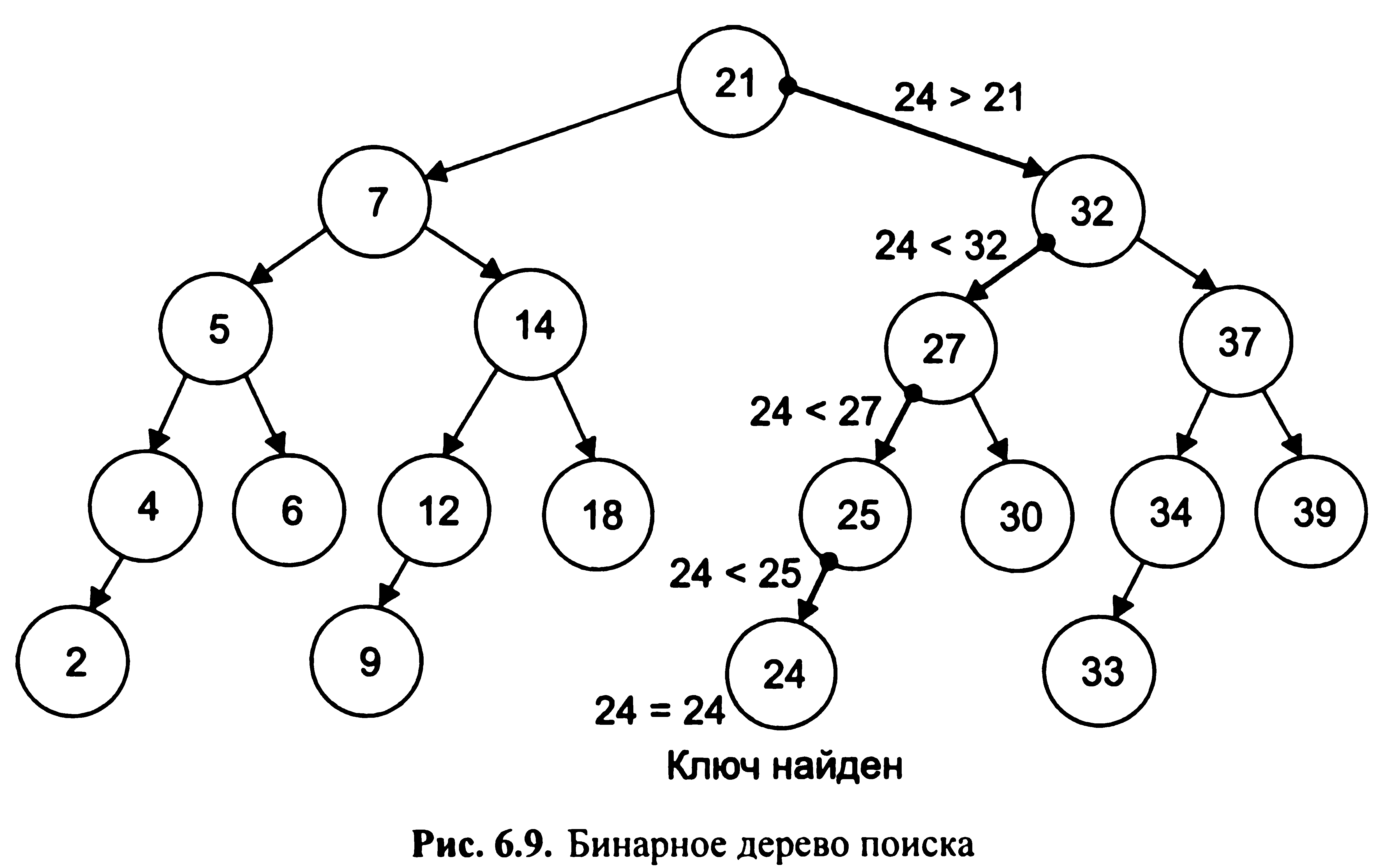 риклад.
Нехай дано вихідна
множина
ключів
{2,
4, 5, 6, 7, 9, 12, 14, 18, 21, 24, 25, 27, 30, 32, 33, 34, 37,
39}.
Вихідна
множина ключів
має бути впорядковано за зростанням.
Від
лінійного списку переходимо до побудови
бінарного дерева пошуку (мал. 6.9). В даному
випадку коренем дерева є центральний
елемент множини
Nэл.та = [п/2]+1, де п - кількість елементів
множини. Вершиною по лівій гілці є
центральний елемент лівого підмножини,
а правою - правого підмножини, і
т.д.
Відшукуваний
ключ = 24.
Вихідна
множина
має 19 елементів. Nэл-та = [19/2] + 1 = 10.
Пошук
ключа К
= 24 по бінарним дереву від кореня до
листя показаний на рис. 6.9.
риклад.
Нехай дано вихідна
множина
ключів
{2,
4, 5, 6, 7, 9, 12, 14, 18, 21, 24, 25, 27, 30, 32, 33, 34, 37,
39}.
Вихідна
множина ключів
має бути впорядковано за зростанням.
Від
лінійного списку переходимо до побудови
бінарного дерева пошуку (мал. 6.9). В даному
випадку коренем дерева є центральний
елемент множини
Nэл.та = [п/2]+1, де п - кількість елементів
множини. Вершиною по лівій гілці є
центральний елемент лівого підмножини,
а правою - правого підмножини, і
т.д.
Відшукуваний
ключ = 24.
Вихідна
множина
має 19 елементів. Nэл-та = [19/2] + 1 = 10.
Пошук
ключа К
= 24 по бінарним дереву від кореня до
листя показаний на рис. 6.9.
П Перетворення довільного дерева в бінарне. Впорядковані дерева ступеня 2 називаються бінарними деревами. Бінарне дерево складається з кінцевого безлічі елементів (вузлів), кожен з яких або порожній, або складається з кореня (вузла), пов'язаного з двома різними бінарними деревами, званими лівим і правим піддерево кореня. Дерева, в яких d > 2, називаються d-арными. Перетворення довільного дерева з впорядкованими вузлами в бінарне дерево зводиться до таких дій. Спочатку в кожному вузлі вихідного дерева викреслюємо всі гілки, крім самих лівих гілок. Після цього в отриманому графі з'єднуємо горизонтальними гілками ті вузли одного рівня, які є «братами» у вихідному дереві. (Пояснимо, що якщо кілька вузлів мають спільного предка, то такі вузли називаються «братами»). В отриманому таким чином дереві лівим нащадком кожного вузла х вважається безпосередньо що знаходиться під ним вузол (якщо він є), а в якості правого нащадка - сусідній праворуч «брат» для х, якщо такий є. На рис. 6.10 показані етапи перетворення таким способом деякого Парного дерева в бінарне.
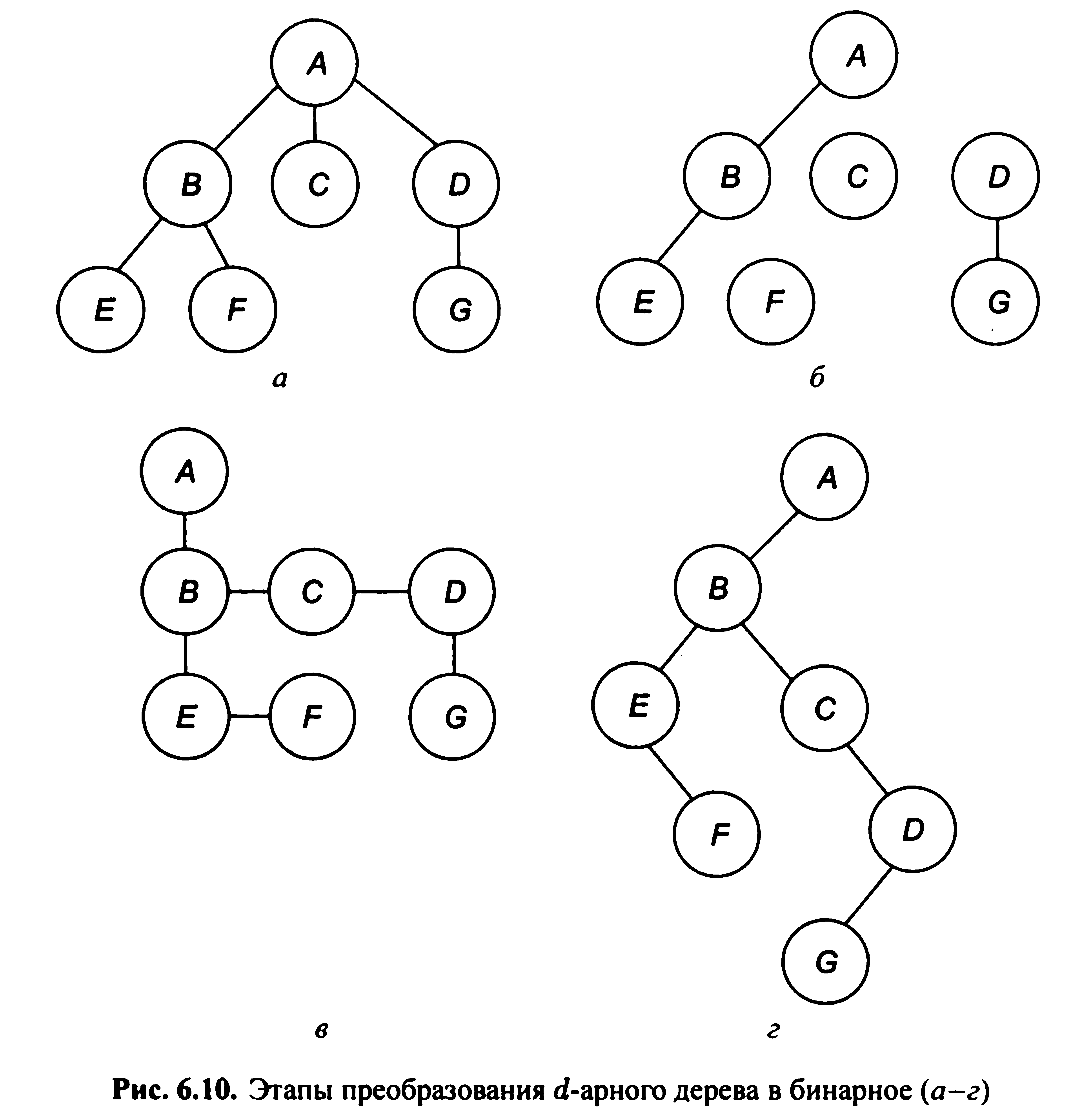
Перехід від довільного дерева до його бінарним еквівалента не тільки полегшує аналіз логічної структури, але також спрощує машинне подання, тобто фізичну структуру дерева. Збалансоване бінарне дерево. Бінарне дерево називається збалансованим (- balanced)9 якщо висота лівого піддерева кожного вузла відрізняється від висоти правого не більше ніж на 1 (рис. 6.11).
Рис.
6.11. Пример сбалансированного дерева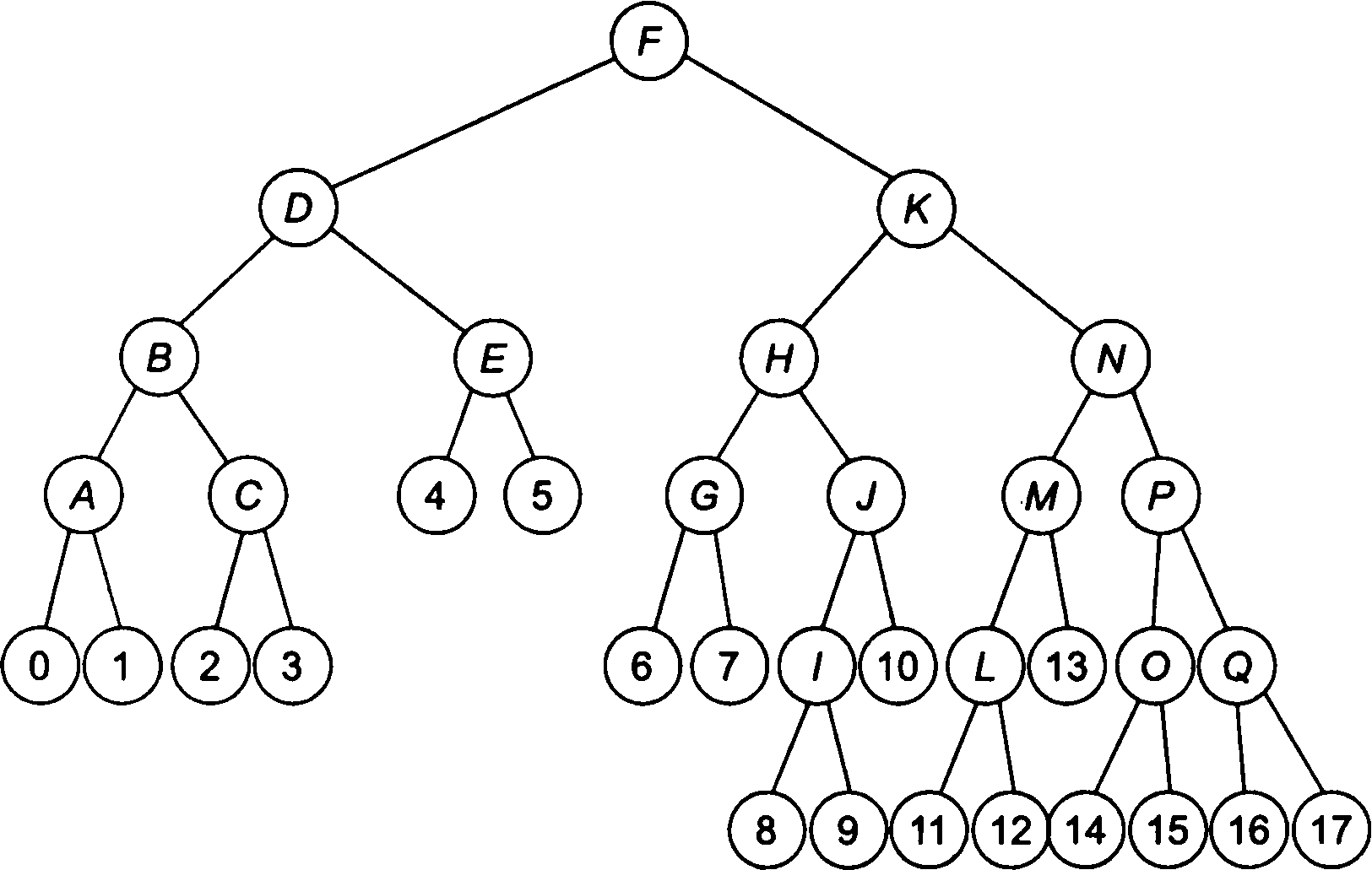
З балансовані
бінарні дерева займають проміжне
положення між оптимальними бінарними
деревами (усі зовнішні вузли яких
розташовані на двох суміжних рівнях) і
довільними бінарними деревами.
Розглянемо
наступну структуру вузлів збалансованого
бінарного дерева (табл. 6.2).
балансовані
бінарні дерева займають проміжне
положення між оптимальними бінарними
деревами (усі зовнішні вузли яких
розташовані на двох суміжних рівнях) і
довільними бінарними деревами.
Розглянемо
наступну структуру вузлів збалансованого
бінарного дерева (табл. 6.2).
- Показник збалансованості вузла, тобто різниця висот правого і лівого піддерева (В = +1; 0; -1). При відновленні балансу дерева по висоті враховується показник (мал. 6.12).

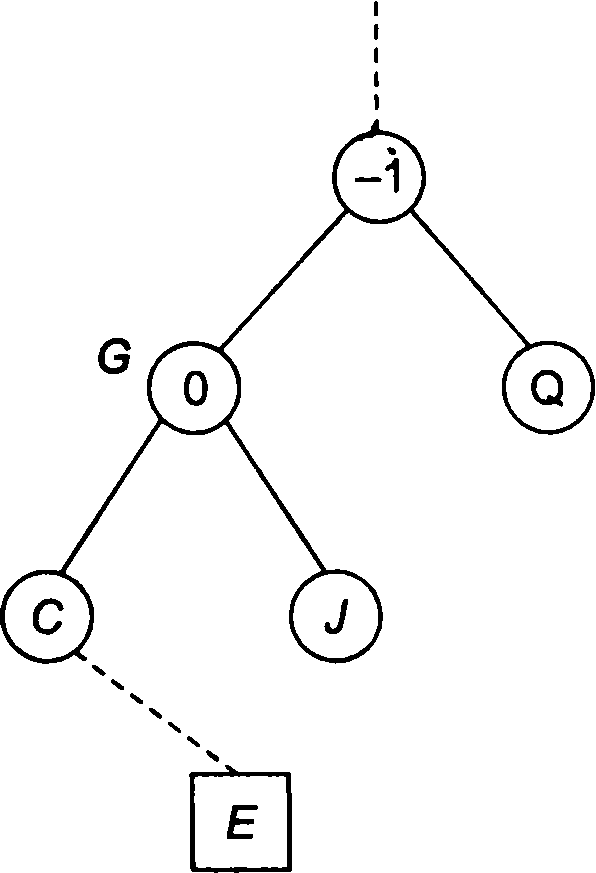
Включаемая
вершина
Рис. 6.12. Деревья с показателями сбалансированности узлов
Символи +1, 0,-1 на рис. 6.12 вказують, що ліве піддерево вище правого, поддеревья рівні по висоті, праве піддерево вище лівого.
6.6.
Пошук по бору
Особливу групу методів пошуку утворює подання ключів у вигляді послідовності цифр і букв. Розглянемо, наприклад, наявні у багатьох словниках буквені висічки. Тоді за першою літерою даного слова можна відшукати сторінки, що містять всі слова, які починаються з цієї букви. Розвиваючи ідею побуквенных висічок, отримаємо схему пошуку, засновану на індексації в структурі бору (термін використовує частину слова вибірка). Бор являє собою m-арное дерево. Кожен вузол до рівня - це безліч всіх ключів, що починаються з певної послідовності з до литер. Вузол визначає m-колійне розгалуження залежно від (h+1)-й літери. Структуру бору можна представити у вигляді таблиці. 6.3.
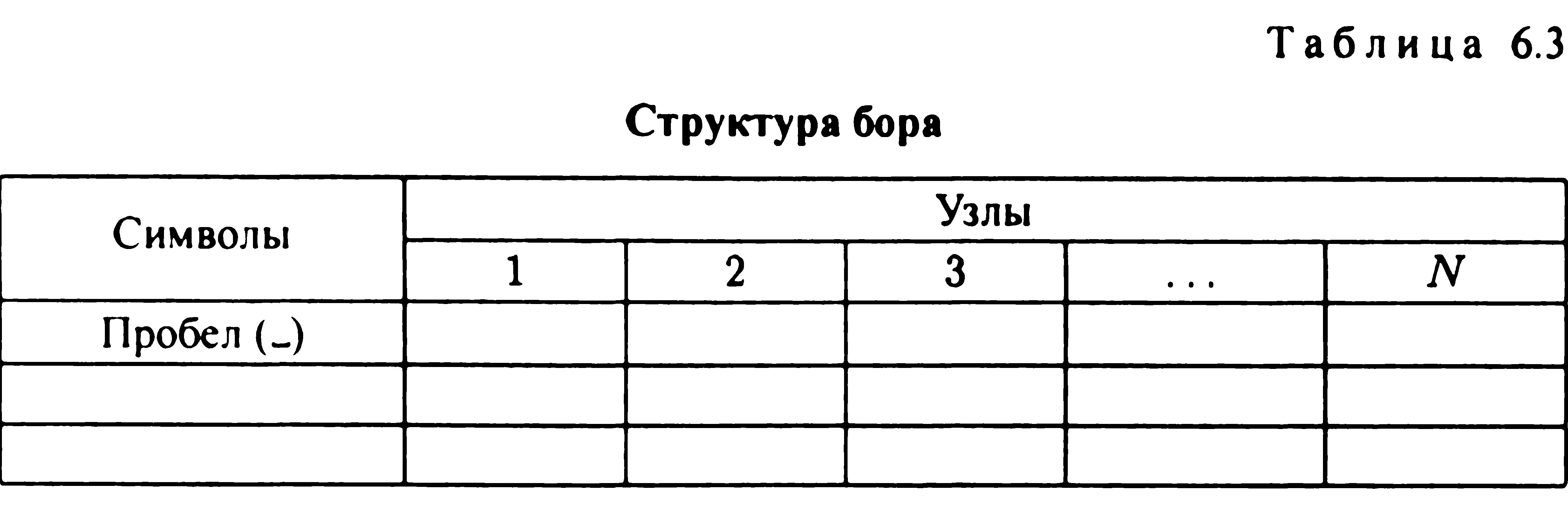
П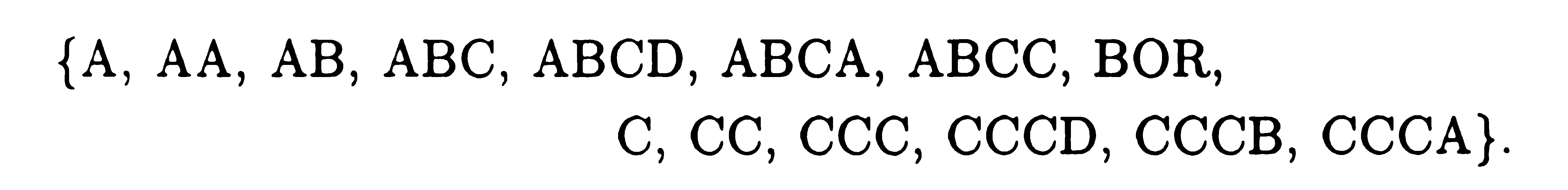 робіл
- обов'язковий символ таблиці.
У
першому вузлі записується перша буква
або цифра ключа. У другому вузлі до неї
додається ще один символ і т.д. Якщо
слово, що починається з певної літери
(цифри), єдине, то воно відразу записується
в першому вузлі.
Приклад
1. Задано множину
робіл
- обов'язковий символ таблиці.
У
першому вузлі записується перша буква
або цифра ключа. У другому вузлі до неї
додається ще один символ і т.д. Якщо
слово, що починається з певної літери
(цифри), єдине, то воно відразу записується
в першому вузлі.
Приклад
1. Задано множину
В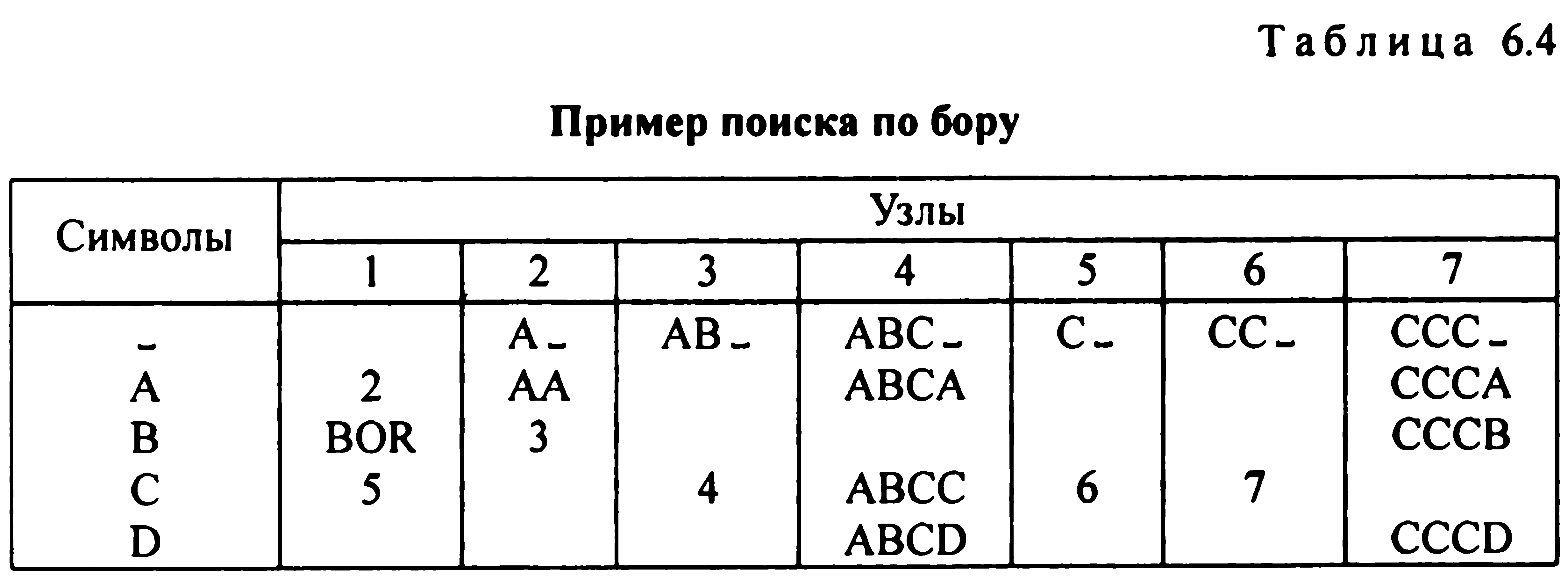 ід
вихідного безлічі перейдемо до побудови
бору. Вихідний алфавіт-{А, В, С, D).
ВОR
- єдине слово на букву, і воно побуквенно
не розбивається.
Вузли
бору являють собою вектори, кожна з
яких являє собою ключ, або посилання
(можливо порожню)- табл. 6.4.
ід
вихідного безлічі перейдемо до побудови
бору. Вихідний алфавіт-{А, В, С, D).
ВОR
- єдине слово на букву, і воно побуквенно
не розбивається.
Вузли
бору являють собою вектори, кожна з
яких являє собою ключ, або посилання
(можливо порожню)- табл. 6.4.
Вузол 1 - корінь, і першу літеру слід шукати тут. Якщо першої виявилася, наприклад, буква В, то з таблиці видно, що йому відповідає слово ВОR. Якщо ж перша літера А, то перший вузол передає управління до вузла 2, де аналогічним чином відшукується друга буква. Вузол 2 вказує, що другими літерами будуть ~ (пробіл), А, В і т.д. Приклад 2. Нехай задано кількість слів: віск, сік, оса, сто, сівши, вік, ост, сотка. Побудуємо m-арное дерево для цього списку (мал. 6.13).
Рис.
6.13. m-арное
дерево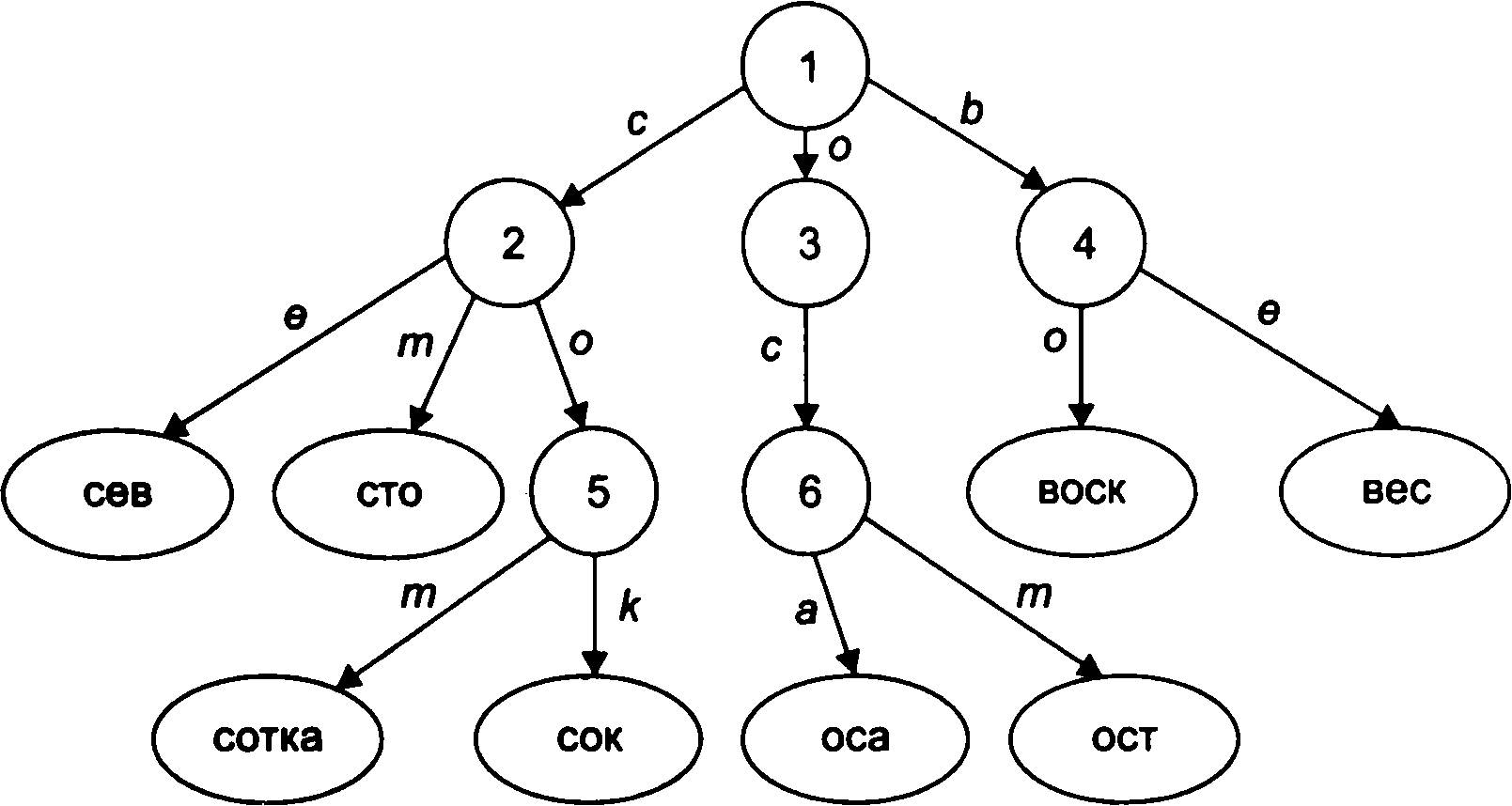
Н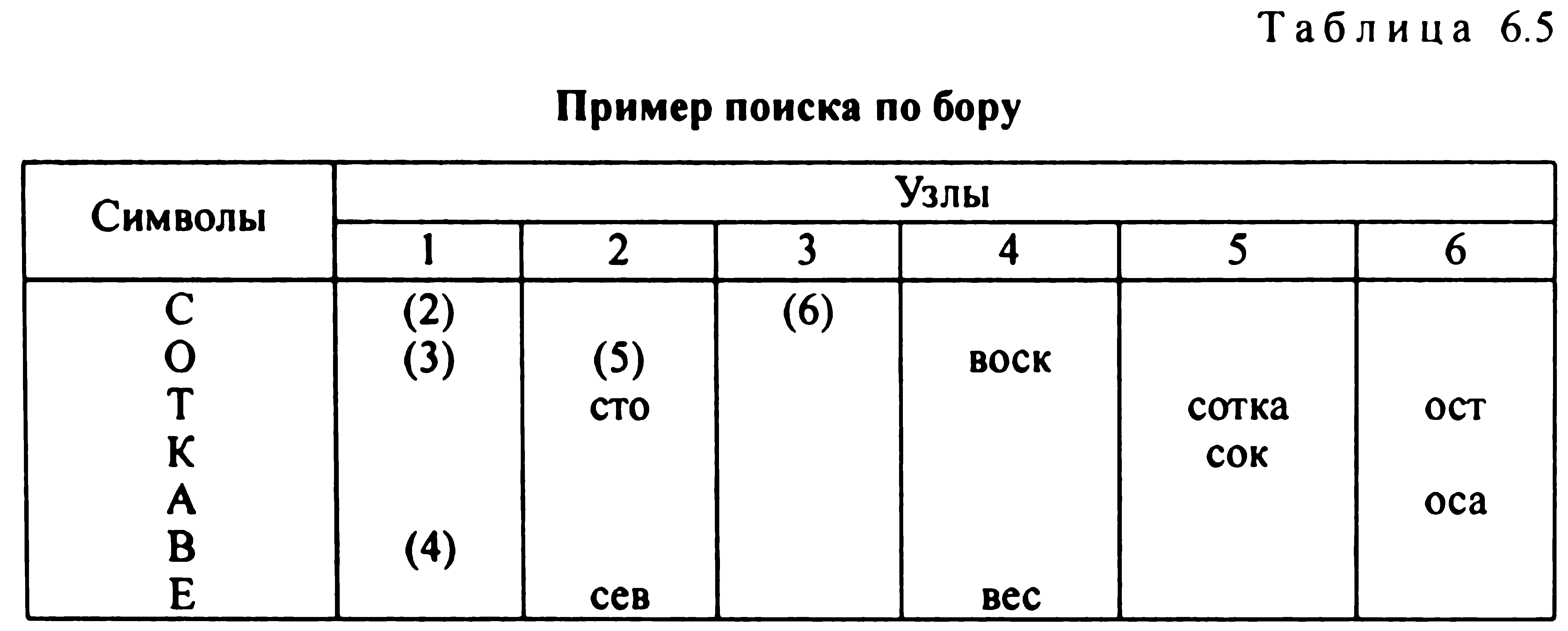 а
основі
аналізу
цього
дерева може бути
побудована
табл. 6.5.
а
основі
аналізу
цього
дерева може бути
побудована
табл. 6.5.
Слід зазначити, що при побудові бору порядок букв у першому стовпці таблиці може бути довільним. Природно, що для кожного конкретного порядку букв заповнення таблиці буде різним. Припустимо, для нашого прикладу в списку слів потрібно знайти слово «ост». Слово починається на літеру «о». Дивимося перетин першого стовпчика з рядком, позначеної на літеру «о». Там записана посилання (3); отже, звертаємося до третій колонці бору. Друга буква слова «ост» - літера «с». На перетині третього стовпці та рядки з буквою «з» записано посилання (6), яка відправляє нас на перегляд шостого стовпчика бору. У цьому стовпці бачимо два слова: «ост» і «оса». Але оскільки третій буквою шуканого слова є літеру «т», то на рядку, позначеної цієї буквою, знаходимо слово «ост».
6.7.
Пошук хешуванням

Рис.
6.14. Устранение коллизий методом цепочек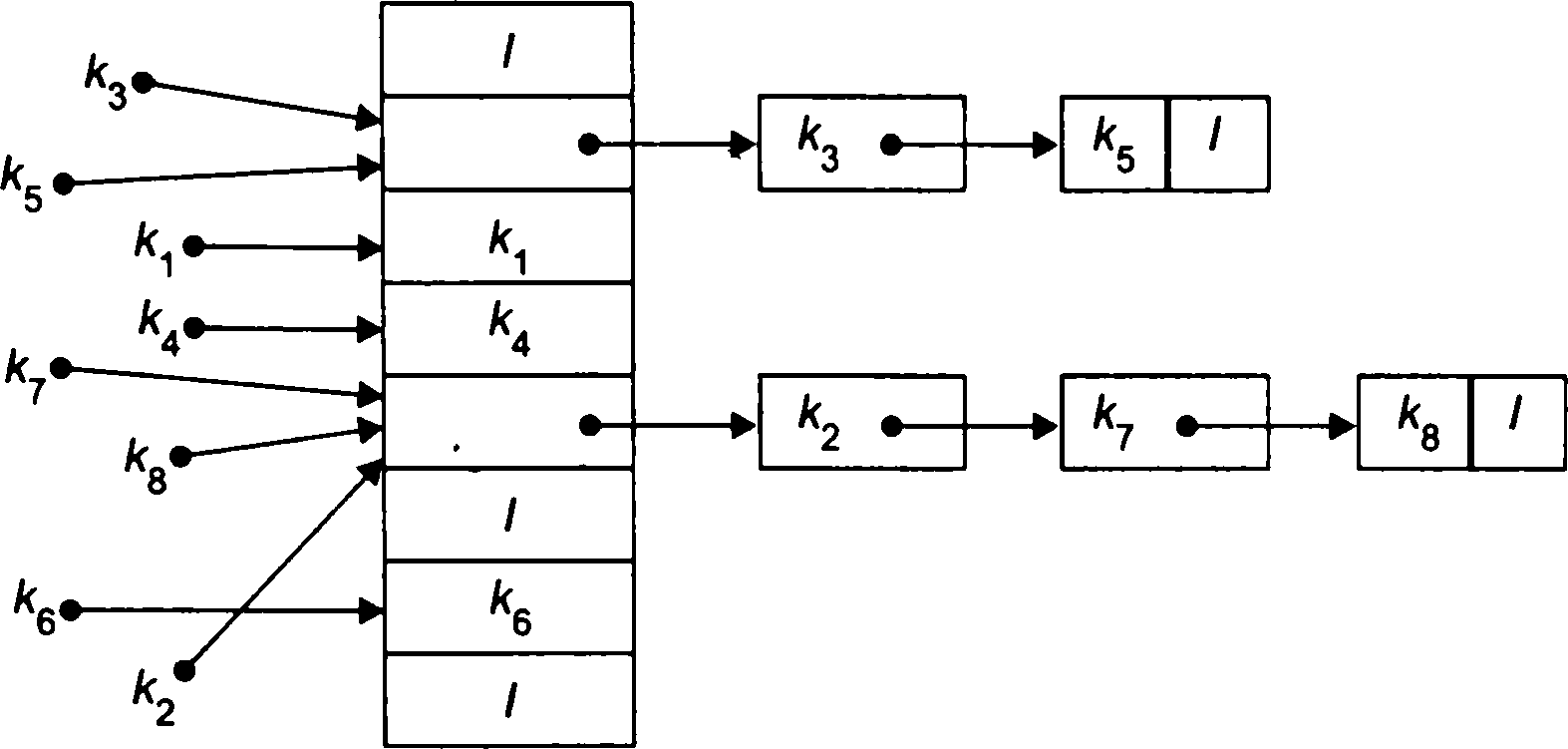
Таблица
6.6
h(k)
Цепочки
ключей
h(k)
Цепочки
ключей
0
6
3
3,9
1
7,13
4
4
2
8
5
5
Попарні порівнянням множини хеш функцій і множини вихідних ключів заповнюємо таблицю. При цьому хеш-функція вказує адресу, за якою слід відшукувати ключ. Наприклад, якщо знаходиться ключ К = 27, тоді h(k) = 27 mod 6 = 3. Це означає, що ключ К = 27 може перебувати тільки у рядку, де h(k) = 3. Так як його там нема, то цей ключ відсутній у вихідному множині. Приклад 2. Дано багато ключів {7, 1, 8, 5, 14, 9, 16, 3, 4}. Знайти ключ К = 14. Хеш-функція дорівнює h(k) = k mod m, де т = [16/2] = 8 (бо 16 - максимальний ключ). Отже, h(k) = {7, 1, 0, 5, 6, 1, 0, 3, 4}. Для вирішення колізій, які присутні в множині хеш функцій, побудуємо табл. 6.7.
Таблица
6.7
h(k)
Цепочки
ключей
h(k)
Цепочки
ключей
0
8,16
5
5
1
1,9
6
14
3
3
7
7
4
4
При заповненні таблиці встановимо відповідність між вихідним безліччю і безліччю хеш функцій. Пошук здійснюється по таблиці: К = 14; h(k) = 14 mod 8 = 6. Це означає, що ключ К= 14 може бути тільки в рядку зі значенням h(k) = 6.
6.8.
Алгоритми пошуку словесної інформації
В даний час наявність надпродуктивних мікропроцесорів і дешевизна електронних компонентів дозволяють робити значні успіхи в алгоритмичній моделюванні. Розглянемо декілька алгоритмів обробки слів.

Іншими словами, потрібно визначити початку Z слова х[1]...х[i + 1], які одночасно є його кінцями. З них слід вибрати найбільш довге (мал. 6.15).
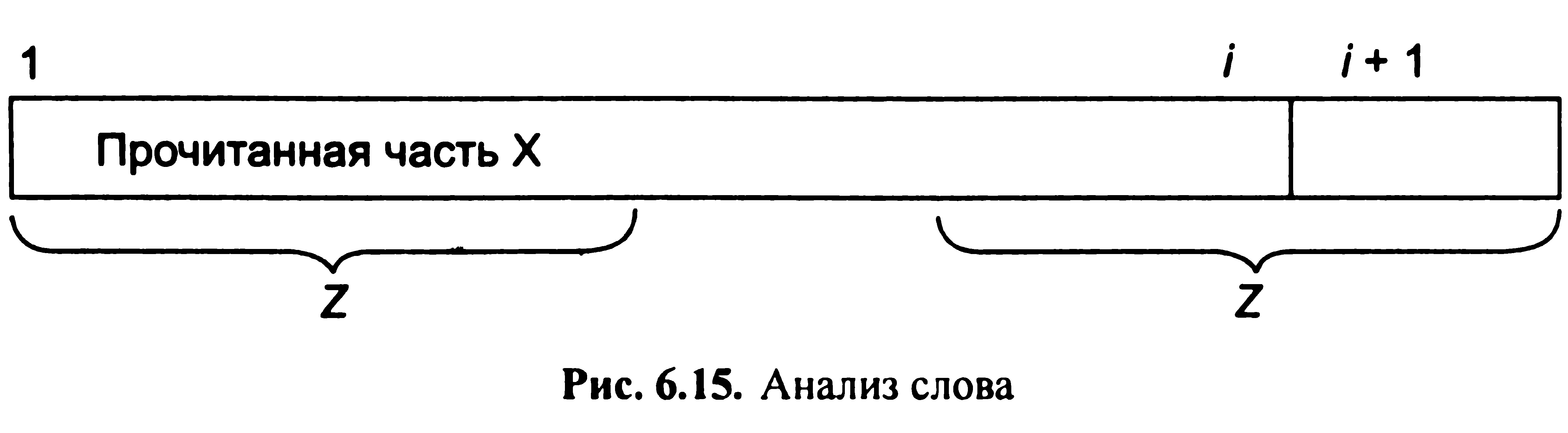
Отримуємо такий спосіб відшукання слова Z. Розглянемо всі початку слова х[1].. .х[i], що є одночасно його кінцями. З них виберемо підходящі - ті, за якими слідує буква х[i + 1]. З відповідних виберемо найдовше. Приписавши в його кінець х[i+1], отримаємо шукане слово Z. Тепер пора скористатися зробленими приготуваннями і згадати, що всі слова, які є одночасно початками і кінцями даного слова, можна отримати повторними застосуваннями до нього функції l. Отримаємо наступний фрагмент програми.

Уявімо алгоритм, який дозволяє перевірити, чи є слово X = x[1]. ..х[n] подсловом слова = [1]...[т]. Рішення. Обчислюємо таблицю l[1]... 1[n], як раніше.

Алгоритм Боєра - Мура (БМ). Цей алгоритм робить те, що на перший погляд здається неможливим: у типовій ситуації він читає лише невелику частину всіх букв слова, в якому шукається заданий зразок. Нехай, наприклад, відшукується зразок abcd. Подивимося на четверту літеру слова: якщо, приміром, це буква е, то немає ніякої необхідності читати перші три букви. (Насправді, у зразку букви е ні, тому він може початися не раніше п'ятої літери.) Наведемо найпростіший варіант цього алгоритму, який не гарантує швидкого роботи у всіх випадках. Нехай х[1]...х[n] - зразок, який треба шукати. Для кожного символу S знайдемо саме праве його входження в слово X, тобто найбільше k, при якому х[k] = s. Ці відомості будемо зберігати в масиві роs[s]; якщо символ s зовсім не зустрічається, то буде зручно припустити роs[s] = 0. Рішення.

Алгоритм Рабіна. Цей алгоритм заснований на простий ідеї. Уявімо собі, що в слові довжиною т шукається зразок довжиною n. Виріжемо віконце розміром п і будемо рухати його з вхідного речі. При цьому перевіряємо, чи не співпадає слово у віконці з заданим зразком. Порівнювати по буквах довго. Замість цього фіксуємо певну функцію, визначену на словах довжиною п. Якщо значення цієї функції на слові у віконці і на зразку різні, то збігу немає. Тільки якщо значення однакові, потрібно перевіряти збіг по буквах. Виграш при такому підході полягає в наступному. Щоб обчислити значення функції на слові у віконці, потрібно прочитати всі букви цього слова. Так вже краще їх відразу порівняти з зразком. Проте можливий виграш, так як при зрушенні віконця слово не змінюється повністю, а лише додається літера в кінці і забирається на початку. Замінимо всі букви в слові і зразку їх номерами, що представляють собою цілі числа. Тоді зручною функцією є сума цифр. (При зміні віконця потрібно додати нове число і відняти зникла.) Виберемо деяке число р (бажано просте) та деякий вирахування х по модулю р. Кожне слово довжиною п представимо як послідовність цілих чисел (замінивши букви кодами). Ці числа будемо розглядати як коефіцієнти багаточлена ступеня п - 1 і обчислимо значення цього многочлена по модулю р в точці х. Це і буде одна з функцій сімейства (для кожної пари р їх виходить, таким чином, свою функцію). Зсув віконця на 1 відповідає вирахуванню старшого члена (хn-1 слід розрахувати заздалегідь), множення на х і додаванню вільного члена. Таке міркування говорить на користь того, що збіги не дуже вірогідні. Нехай число р фіксовано і до того ж просте, а X і У - два різних слова довжиною п. Тоді їм відповідають різні многочлени (припускаємо, що коди всіх букв різні - це можливо, якщо р більше числа букв алфавіту). Збіг значень функції означає, що в точці х ці два різних багаточлена збігаються, тобто їх різниця звертається до 0. Різниця є многочлен ступеня п - 1 і має не більше п - 1 коренів. Таким чином, якщо п багато менше р, у випадкового х мало шансів потрапити в невдалу точку.
Контрольні питання 1. Що розуміється під пошуком? 2. Які особливості послідовного і бінарного пошуку? 3. Які особливості інтерполяційного і фибоначчиевого пошуку? 4. Які особливості пошуку по бінарним дереву? 5. Які особливості пошуку по бору і хешированием? 6. У чому полягає методика аналізу складності алгоритмів пошуку? 7. У чому полягає особливість алгоритмів пошуку словесної інформації? 8. Що таке колізія? 9. Який метод використовується для вирішення колізій? 10. Що визначає показник збалансованості вузла дерева? 11. Назвіть алгоритми пошуку словесної інформації.
