Зміст Передмова ……………………………………………………………………………..7 Частина 1. Основи алгоритмізації …………………………………………………9 Глава 1. Структурна організація даних …………………………………………..9 1.1. Основні поняття структур даних………………………………………………9 1.2. Класифікація структур даних за ознакою мінливості …………………….12 1.3. Лінійні і нелінійні структури даних……………………………………………...13 Контрольні питання…………………………………………………………………….. 19 Глава 2. Моделі об'єктів і процесів ……………………………………………………20 2.1. Моделі структурні і функціональні ……………………………………………….22 2.2. Моделі натурні та інформаційні ……………………………………………………23 2.3. Класифікація моделей ……………………………………………………………….25 2.4. Етапи моделювання ………………………………………………………………….26 2.5. Властивості алгоритму ………………………………………………………………27 2.6. Види алгоритмів та їх реалізація …………………………………………………...28 2.7. Базові канонічні структури алгоритмів .................................................................. 34 2.8. Повне побудова алгоритму ………………………………………………………….38 2.9. Головні принципи створення ефективних алгоритмів …………………………42 Контрольні питання …………………………………………………………………………44 Глава 4. Функція складності ………………………………………………………………….49 4.1. Види функції складності алгоритмів …………………………………………………..52 4.2. Тимчасова функція складності …………………………………………………………53 4.3. Аналіз функції складності по програмі ………………………………………………...53 4.4. Оцінка алгоритму бінарного пошуку ……………………………………………………55 4.5. Теоретична та практична функції складності …………………………………………56

Контрольні питання …………………………………………………………………….58 Частина 2. Алгоритми обробки структур даних . . . ………………………………59 Глава 5. Методи сортування …………………………………………………………..59 5.1. Сортування вибором ……………………………………………………………….60 5.2. Сортування вставкою і сортування злиттям ... ……………………………….61 5.3. Сортування обміном і шейкерне сортування ... ……………………………..63 5.4.Сортування Користувача ……………………………………………………………66 5.5. Швидке сортування (сортування Хоара) ………………………………………...68 5.6. Турнірна сортування 69 5.7. Пірамідальна сортування 71 Контрольні питання 73 Глава 6. Методи пошуку 74 6.1. Послідовний пошук 75 6.2. Бінарний пошук 76 6.3. Фибоначчиев пошук 78 6.4. Інтерполяційний пошук 79 6.5. Пошук за бінарним дереву 81 6.6. Пошук за бору 87 6.7. Пошук хешированием 90 6.8. Алгоритми пошуку словесної інформації 92 Контрольні питання 96 Глава 7. Ітеративні і рекурсивні алгоритми .... 97 7.1. Ітеративний алгоритм 98 7.2. Рекурсивні алгоритм 100 7.3. Рекурсивні структури даних 103 7.4. Види обходу бінарних дерев 107 Контрольні питання 109 Глава 8. Основні визначення теорії графів 110 8.1. Ізоморфізм графів 113 8.2. Ступінь вершини графа 115 8.3. Поняття підграфа 119 8.4. Цикли на графі 119 8.5. Цикломатичне число графа 124 8.6. Подання графів PC 127 Контрольні питання 130 Глава 9. Алгоритми побудови кістяка (що покриває) дерева мережі 131 9.1. Метод Крускала 134 9.2. Метод Прима 141 Контрольні питання 144 Розділ 10. Алгоритми знаходження на графах найкоротших шляхів 145 10.1. Побудова дерева рішень 145 10.2. Метод динамічного програмування 148 10.3. Метод Дейкстри . 154 10.4. Алгоритм Флойда 157 10.5. Алгоритм Ієна 158 10.6. Алгоритм Беллмана - Ford 160 Контрольні питання 161 Глава 11. Евристичні алгоритми 162 11.1. Хвильовий алгоритм 162 11.2. Двопроміневий алгоритм 165 11.3. Четырехлучевой алгоритм 167 11.4. Маршрутний алгоритм 168 11.5. Геометрична модель задачі про лабіринті .... 170 11.6. Алгоритми складання розкладу 173 11.7. Завдання упаковки 175 11.8. Завдання про джипі 178 11.9. Завдання про кодовому замку 181 Контрольні питання 183 Глава 12. Метод галузей і границь. Завдання комівояжера . 184 12.1. Розшифровка криптограмм 186 12.2. Завдання про радіоактивне кулі 189 12.3. Завдання комівояжера 190 12.4. Приклади розв'язання задачі комівояжера 195 Контрольні питання 210 Розділ 13. Моделювання з використанням генераторів випадкових чисел 211 13.1. Числові характеристики випадкових величин . . . 211 13.2. Метод середини квадрата 212 13.3. Лінійний конгруэнтный метод 213 13.4. Полярний метод генерації випадкових чисел . . . 215 Контрольні питання 216 Глава 14. Машина Тьюринга 216 14.1. Структура машини Тьюринга 218 14.2. Функціональні таблиці та діаграми 219 14.3. Приклади запису алгоритмів 222 14.4. Композиція машин Тьюринга 224 Контрольні питання 227 Глава 15. Елементи математичної логіки 227 15.1. Алгебра висловлювань 228 15.2. Закони математичної логіки 235 15.3. Рішення логічних завдань 236 15.4. Логічної основи PC 258 15.5. Логічний синтез обчислювальних схем 261 15.6. Подання логічної функції у вигляді графа . 263 15.7. Перевірка правильності висновків з серії посилок 264 Контрольні питання 266

Лекція 1.

Тема: ОСНОВИ АЛГОРИТМІЗАЦІї

Основні поняття структур данних

Комп'ютер оперує тільки з одним видом даних - з окремими бітами, або двійковими цифрами, і працює з цими даними тільки у відповідності з незмінним набором алгоритмів, які визначаються системою команд центрального процесора. Завдання, що вирішуються за допомогою комп'ютера, рідко виражаються мовою бітів. Як правило, дані мають форму чисел, литер, текстів, символів і більш складних структур типу послідовностей, списків і дерев. Ще різноманітніше алгоритми, які використовуються для вирішення різних завдань; фактично алгоритмів не менше, ніж обчислювальних завдань.

Структура даних, розглянута без урахування її подання в машинної пам'яті, називається абстрактною, або логічної. Поняття «фізична структура даних» відображає спосіб фізичного подання даних у машинній пам'яті. Внаслідок відмінності між логічної і відповідної їй фізичної структурами в комп'ютерній системі існують процедури, які здійснюють відображення логічної структури в фізичну, і навпаки. Наприклад, доступ до елемента двомiрного масива на логічному уроь*,з реалізується зазначенням номерів рядка та стовпчика в прямокутної таблиці, на перетині яких розташований відповідний елемент. На фізичному рівні до елемента масиву доступ здійснюється за допомогою функції адресації, яка при відомому початковому адресу масиву в машинної пам'яті перетворює номера рядка та стовпчика на адресу відповідного елементу масиву. Таким чином, кожну структуру даних можна характеризувати її логічним (абстрактним) і фізичним (конкретним) уявленнями, а також сукупністю операцій на цих двох рівнях подання структури (мал. 1.1). Дуже часто, кажучи про тій чи іншій структурі даних, мають на увазі її логічне подання, так як фізична подання зазвичай приховується від програміста. Так як фізична структура даних реалізується в машинної пам'яті, що має обмежений обсяг, то при вивченні такої структури повинна враховуватися проблема розподілу і управління пам'яттю. Структури даних, застосовувані в алгоритмах, можуть бути надзвичайно складними. В результаті вибір правильного подання даних часто служить ключем до вдалому програмування і може більшою мірою позначатися на ефективності програми, ніж деталі використовуваного алгоритму. Під структурою даних у загальному випадку розуміють безліч елементів даних і безліч зв'язків між ними. Таке визначення охоплює всі можливі підходи до структуризації даних, але

Рис. 1.1. Уровни представления структуры данных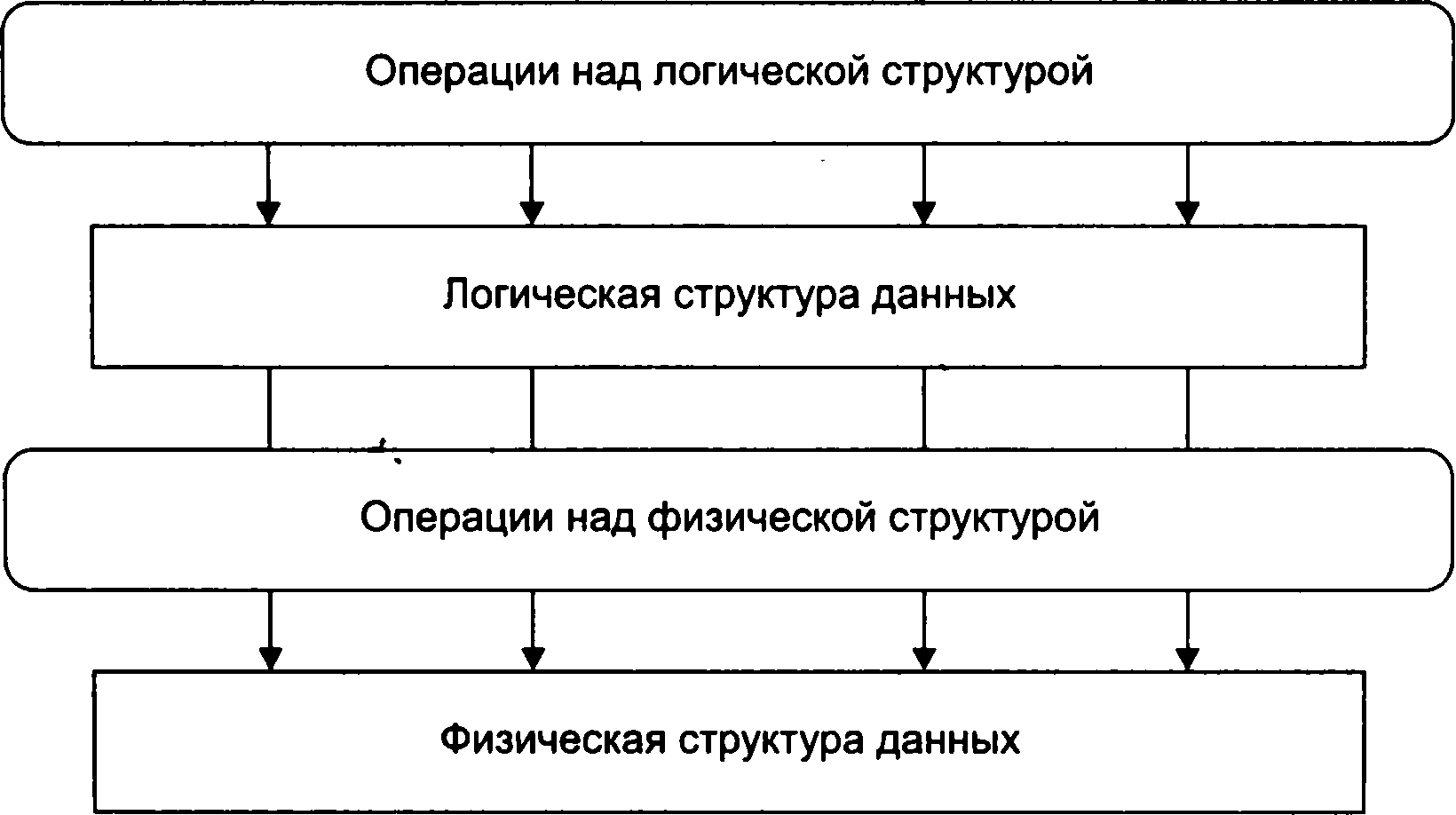

у кожній конкретній задачі використовуються ті або інші його аспекти. Тому вводиться додаткова класифікація структур даних, напрямки якої відповідають різним аспектам їх розгляду. Перш ніж приступати до вивчення конкретних структур даних, дамо їх загальну класифікацію за кількома ознаками. Поняття «фізична структура даних» відображає спосіб фізичного подання даних у пам'яті PC і називається ще структурою зберігання, внутрішньою структурою або структурою пам'яті. Розгляд структури даних без урахування її подання в пам'яті комп'ютера називається абстрактною, або логічною структурою. У загальному випадку між логічної і відповідної їй фізичної структурами існує різниця, ступінь якого залежить від самої структури та особливостей того середовища, в якому вона повинна бути відображена. Внаслідок цього існують відмінності процедури, які здійснюють відображення логічної структури в фізичну і, навпаки, фізичної структури в логічний. Ці процедури забезпечують, крім того, доступ до фізичним структурам і виконання над ними різних операцій, причому кожна операція розглядається стосовно до логічної або фізичної структури даних. Розрізняють прості (базові, примітивні) структури (типи) даних та інтегровані (структуровані, композитні, складні). Простими називаються такі структури даних, які не можуть бути розділені на складові частини, більші, ніж біти. Для фізичної структури важливим є та обставина, що в даній машинної архітектурі і в даній системі програмування завжди можна заздалегідь знати, який буде розмір вибраного простого типу і яка структура його розміщення в пам'яті. З логічної точки зору прості дані є неподільними одиницями. Інтегрованими називаються такі структури даних, складовими частинами яких є інші структури даних - прості або, у свою чергу, інтегровані. Інтегровані структури даних конструюються програмістом з використанням засобів інтеграції даних, що надаються мовами програмування. Залежно від відсутності або наявності явно заданих зв ’ язків між елементами даних слід розрізняти незв'язні структури (вектори, масиви, рядки, стеки, черги) і зв'язні структури (зв'язні списки).

Классифікація структур даних по признаку мінливості

Важлива ознака структури даних - її мінливість, тобто зміна числа елементів і (або) зв'язків між елементами структури. У визначенні мінливості структури не відображено факт зміни значень елементів даних, оскільки в цьому випадку всі структури даних мали б властивість мінливості. За ознакою мінливості розрізняють структури базові, статичні, підлозі статичні, динамічні та файлові. Класифікація структур даних (СД) за ознакою мінливості наведена на рис. 1.2. Базові структури даних, статичні, полустатические і динамічні характерні для оперативної пам'яті і часто називаються оперативними структурами. Файловые структури відповідають структур даних для зовнішньої пам'яті. Вектор (одновимірний масив) - структура даних з фіксованим числом елементів одного і того ж типу.

Рис. 1.2. Классификация структур данных по признаку изменчивости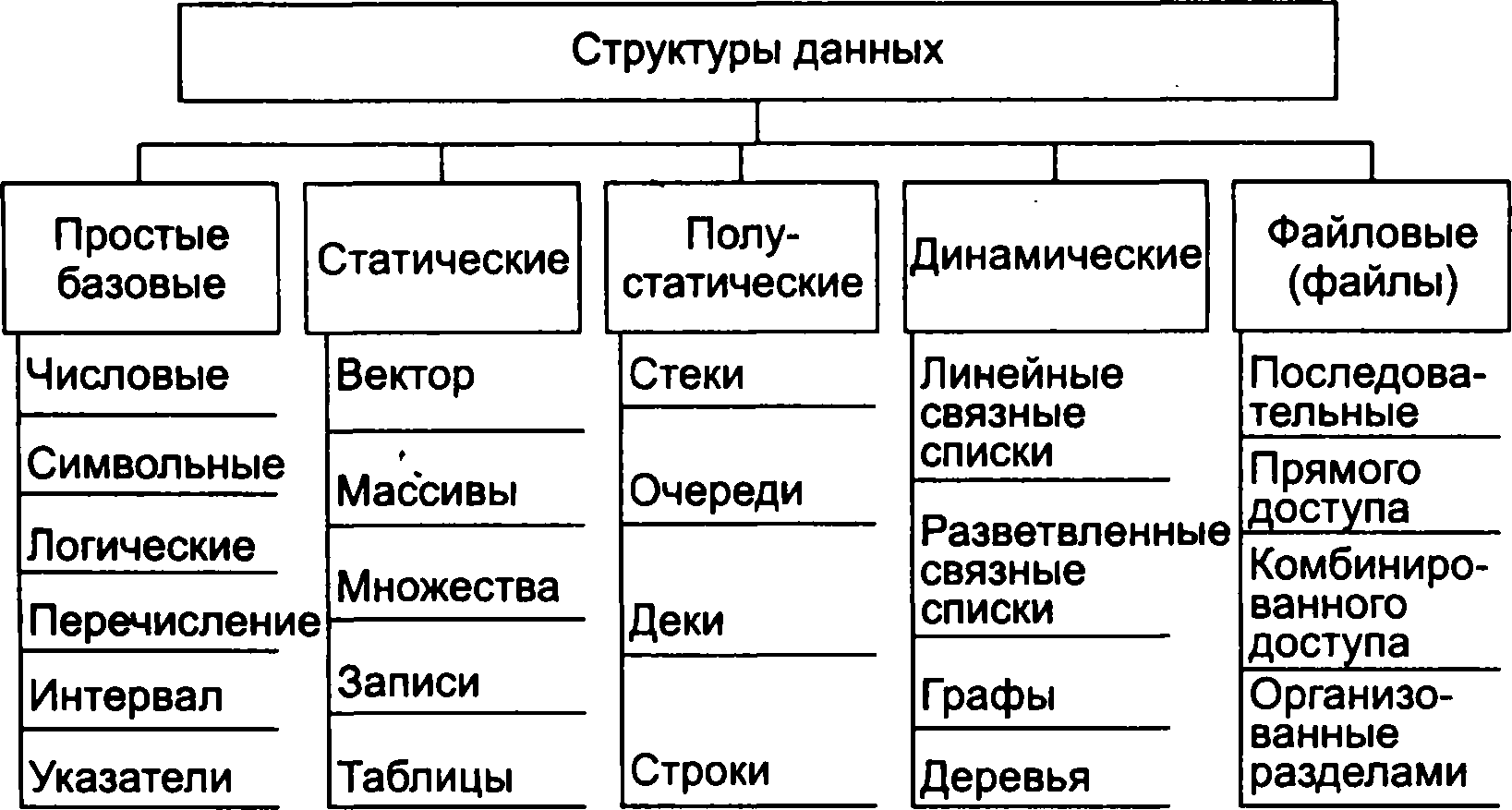

Масив - послідовність елементів одного типу, званого базовим. Множина - така структура, яка являє собою набір неповторюваних даних одного і того ж типу. Запис - кінцеве впорядкована множина полів, що характеризуються різним типом даних. Таблиця - послідовність записів, які мають одну і ту ж організацію. Списком називається впорядкована множина, що складається з змінного числа елементів, до яких застосовуються операції включення, виключення. Список, що відображає ставлення сусідства між елементами, називається лінійним.

1.3.Лінейні та нелінейнійні структури даних

Н агадаємо, що структури даних представляють собою стосунки, задані на множинах даних. Нехай X - безліч даних, У - множина значень даних:

Якщо на множині μ(х) задано відношення S(х) ≥ μ(х) то будемо називати це відношення структурою даних, а - областю визначення структури даних. Структура даних називається простий, якщо між значеннями даних зв'язку відсутні, тобто. S(x) = 0 і μ(х) ≠ 0. Розглянемо різні класифікації структур даних для того, щоб визначити вигляд структур даних, найбільш адекватно що представляють інформацію, а також місце, яке вони займають у загальній системі класифікації структур даних. Важлива ознака структури даних - характер впорядкованості її елементів. За цією ознакою структури можна ділити налинейно-упорядо - чег ле, або лінійні, і нелінійні структури (мал. 1.3).

Рис. 1.3. Линейные и нелинейные структуры данных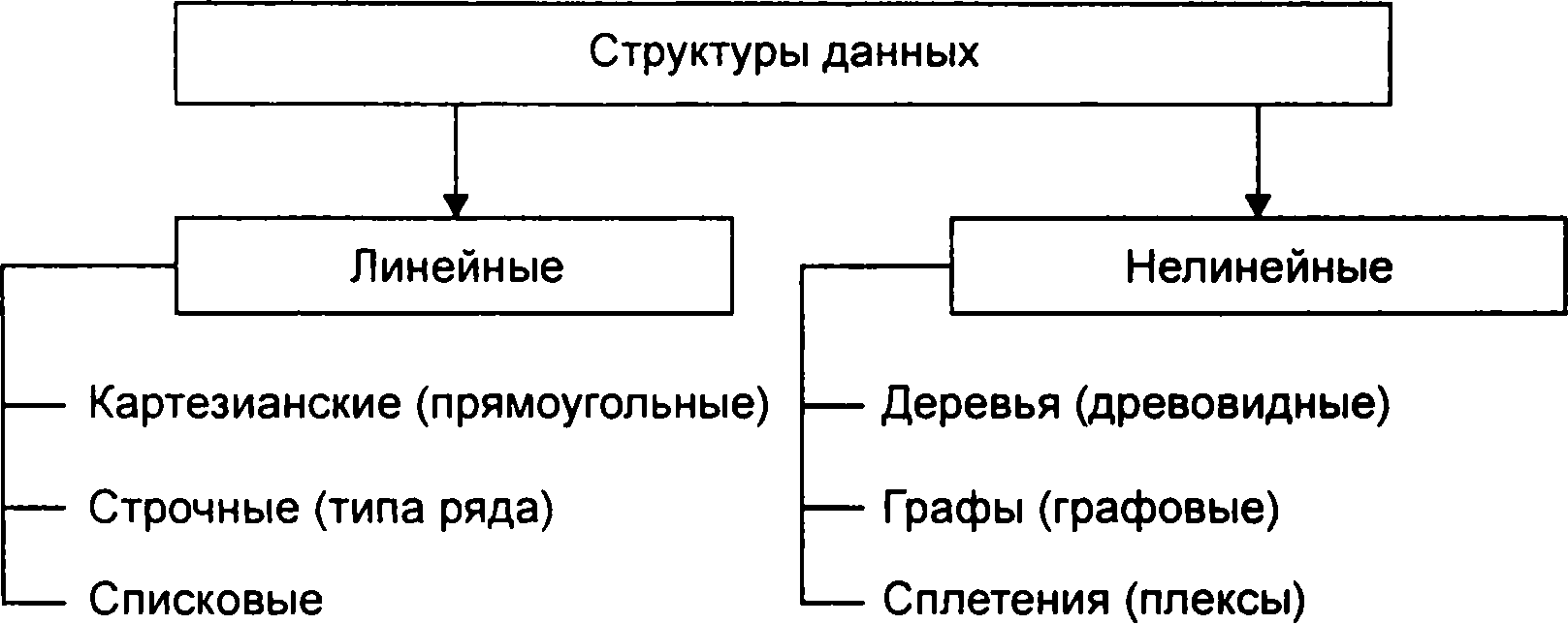

З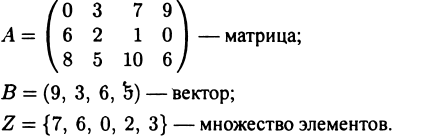 алежно від характеру взаємного розташування елементів пам'яті PC лінійні структури можна розділити на структури з послідовним розподілом їх елементів пам'яті (вектори, рядки, масиви, стеки, черги) і структури з довільним пов'язаних розподілом елементів пам'яті (однозв'язні, двозв'язані і інші списки). Лінійні структури даних. Лінійні структури даних (СД) - це структури, в яких зв'язку між елементами не залежать від виконання якого-або умови. Лінійні структури поділяються на три типи: картезианские, рядкові і списковые. • Картезианские, або прямокутні, структури названі так за способом запису даних у вигляді прямокутних таблиць. Наприклад:

• Рядкові структури - одномірні, динамічно змінні структури даних, що розрізняються способами включення і виключення елементів (мал. 1.4).

Рис. 1.4. Строчные структуры данных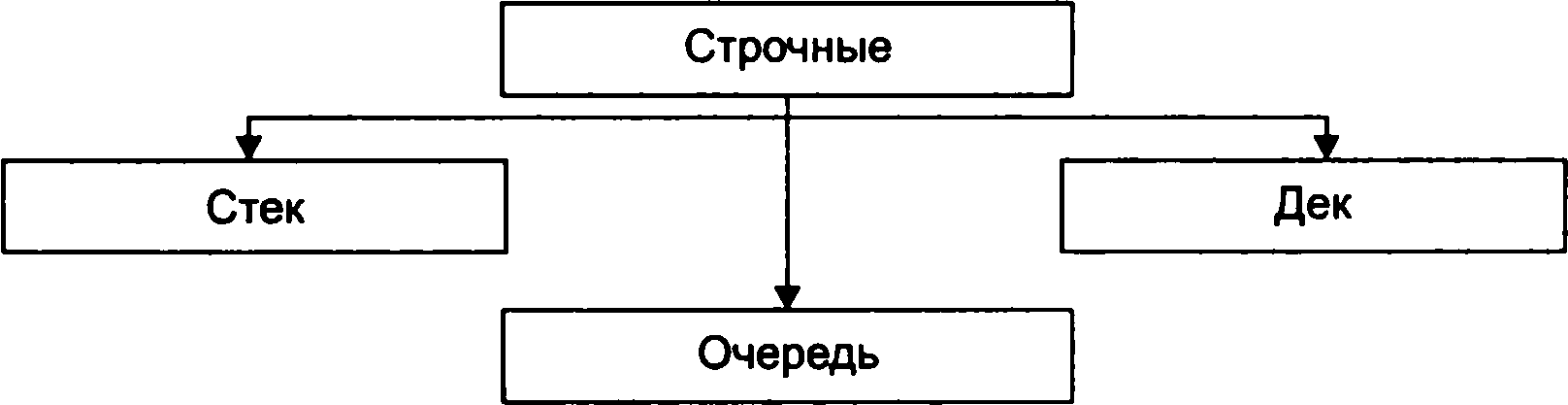

Стек - це послідовність, в якій включення і виключення елемента здійснюється з одного боку послідовності (мал. 1.5).

Рис. 1.5. Схема доступа к элементам стека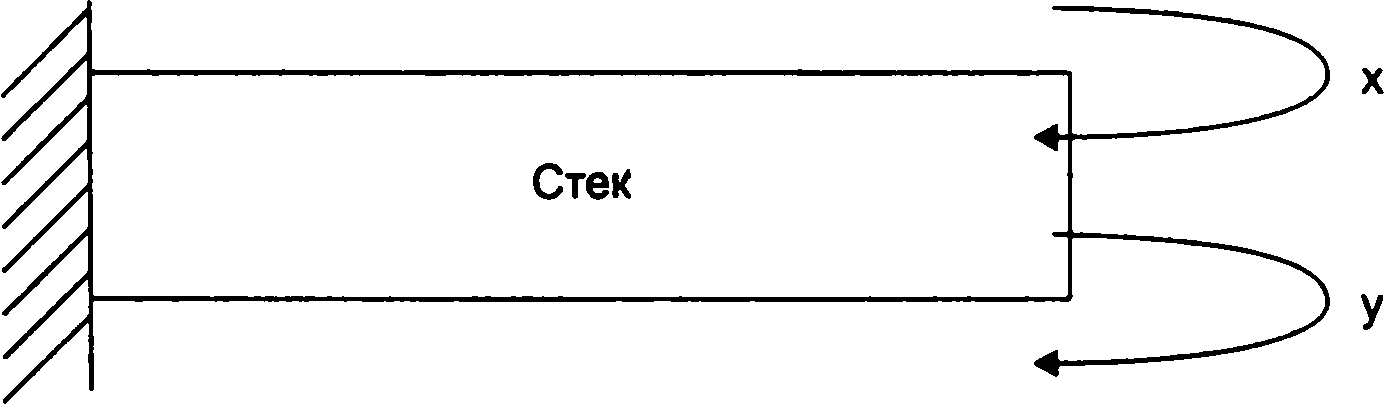

Нехай, наприклад, дано безліч елементів {2, 5, 7, 1,9,3} і задано алгоритм роботи стека (X, X, X, Y, X, Y, Y). Тоді після роботи алгоритму в стеку залишиться число 2. Відомі приклади стека - гвинтівковий патронний магазин, залізничний роз'їзд для сортування вагонів (мал. 1.6).

Вход Выход

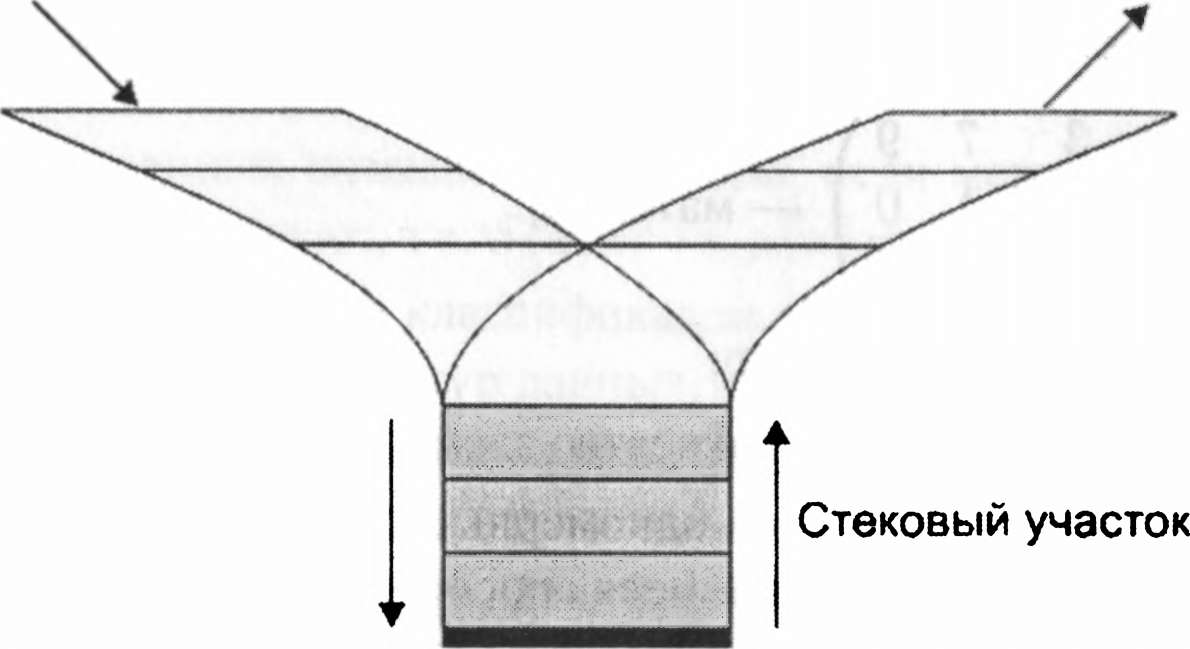
Рис. 1.6. Стек на железных дорогах

Черга - послідовність, в яку включають елементи з одного боку, а виключають - з іншого (мал. 1.7). Структура функціонує за принципом FIFO (першим прийшов - першим обслуговується).

Рис. 1.7. Схема доступа к элементам очереди

Дек - лінійна структура (послідовність), в якій операції включення і виключення елементів можуть виконуватися як з одного, так і з іншого кінця послідовності (мал. 1.8).

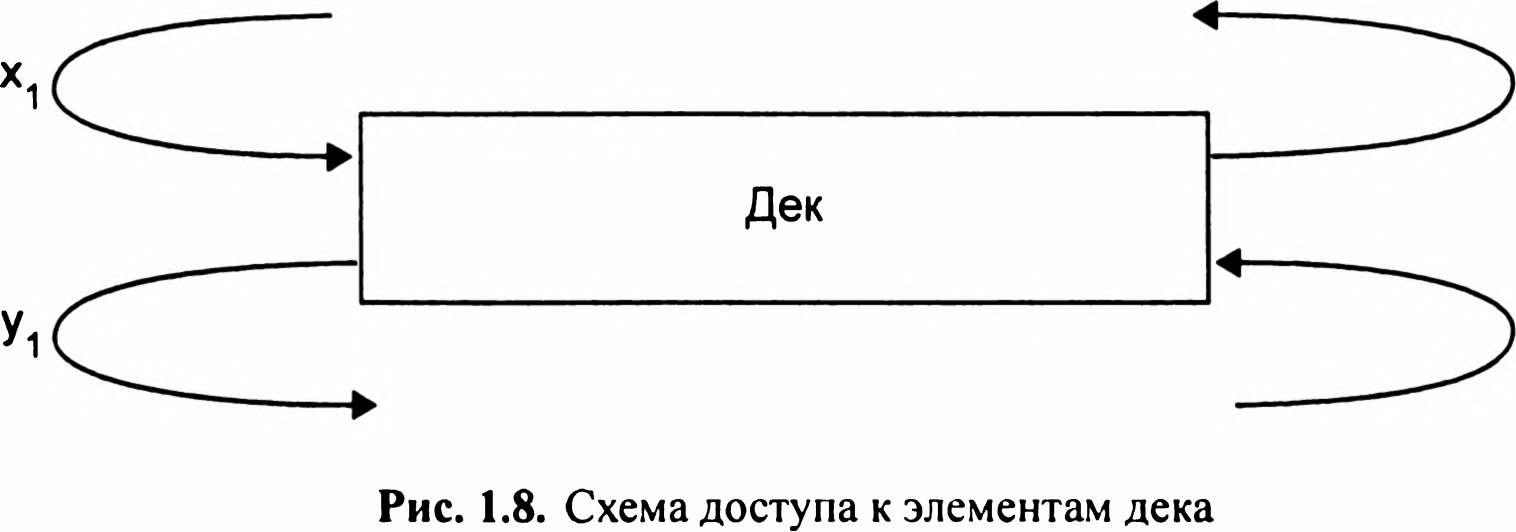
У списковых структурах логічний порядок даних визначається покажчиками. Будь-яка списковая структура являє собою набір елементів, кожен з яких складається з двох полів: в одному з них розміщений елемент даних або вказівник на нього, а в іншому - покажчик на наступний елемент списку. Нелінійні структури даних. Нелінійні структури даних - це СД, у яких зв'язку між елементами залежать від виконання певних умов. Приклади нелінійних структур - дерева, графи, багатозв'язані списки. •Ієрархічні структури - це ієрархічні структури, що складаються з набору*вершин і ребер, кожна вершина містить певну інформацію і посилання на вершину нижнього рівня. Дерево - це сукупність елементів, званих вузлами (один з яких визначено як корінь), і відносин, що утворюють ієрархічну структуру вузлів (мал. 1.9).

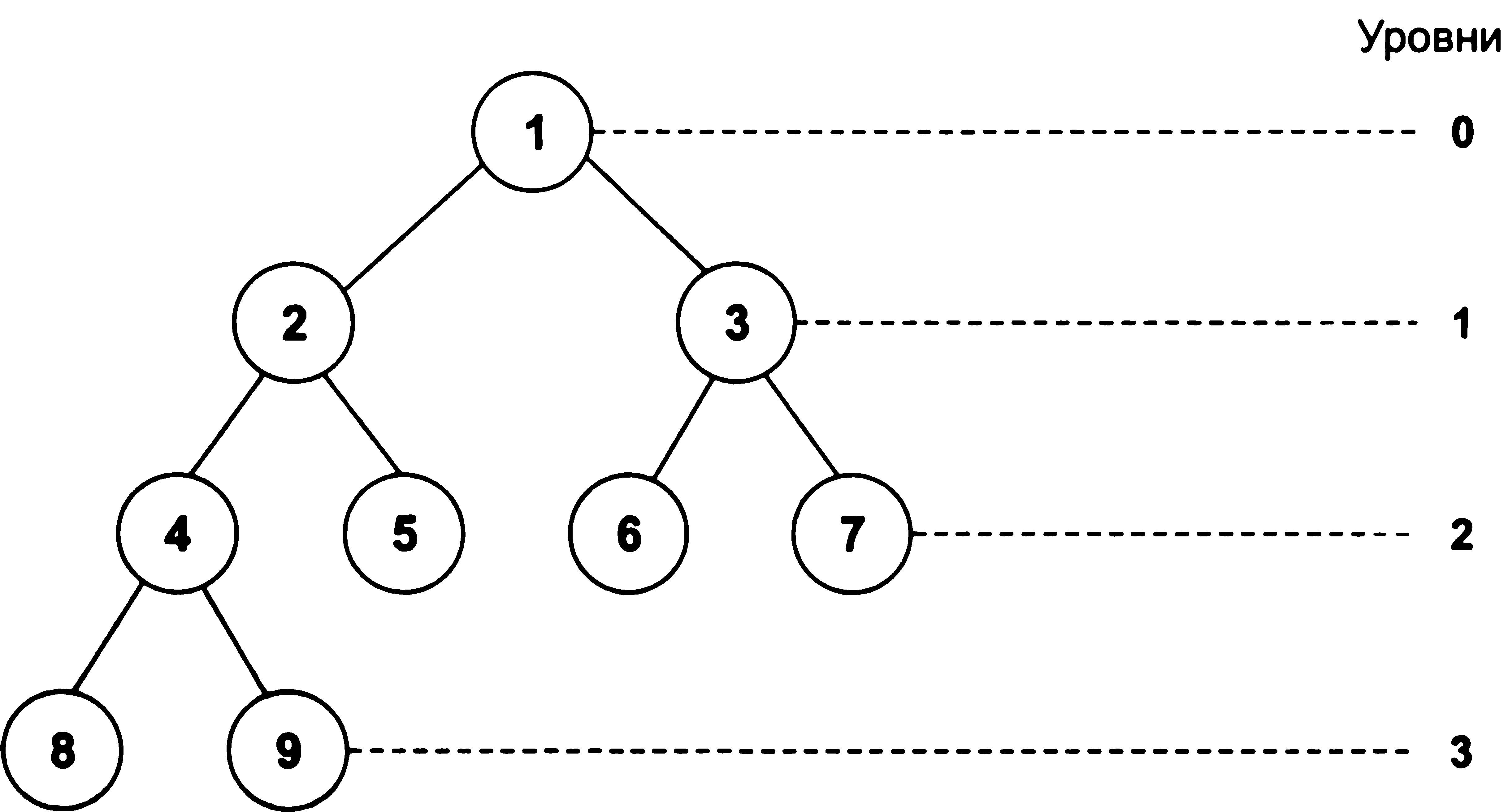
Рис. 1.9. Древовидная структура (дерево)

Вершина, розташована в нульовому рівні, називається коренем дерева (нумерація рівнів може починатися з 1). В корінь не входить ні одного ребра. Вершини, з яких не виходить жодного ребра, називаються листям (вершини 8, 9, 5, 6, 7). Дерево, з кожної вершини якого виходить тільки за два ребра, називається бінарним (мал. 1.10). • Графи являють собою сукупність двох множин: вершин і ребер. Граф - це складна нелінійна багатозв ’ язна динамічна структура, яка відображає властивості і зв'язку складного об'єкта (мал. 1.11).

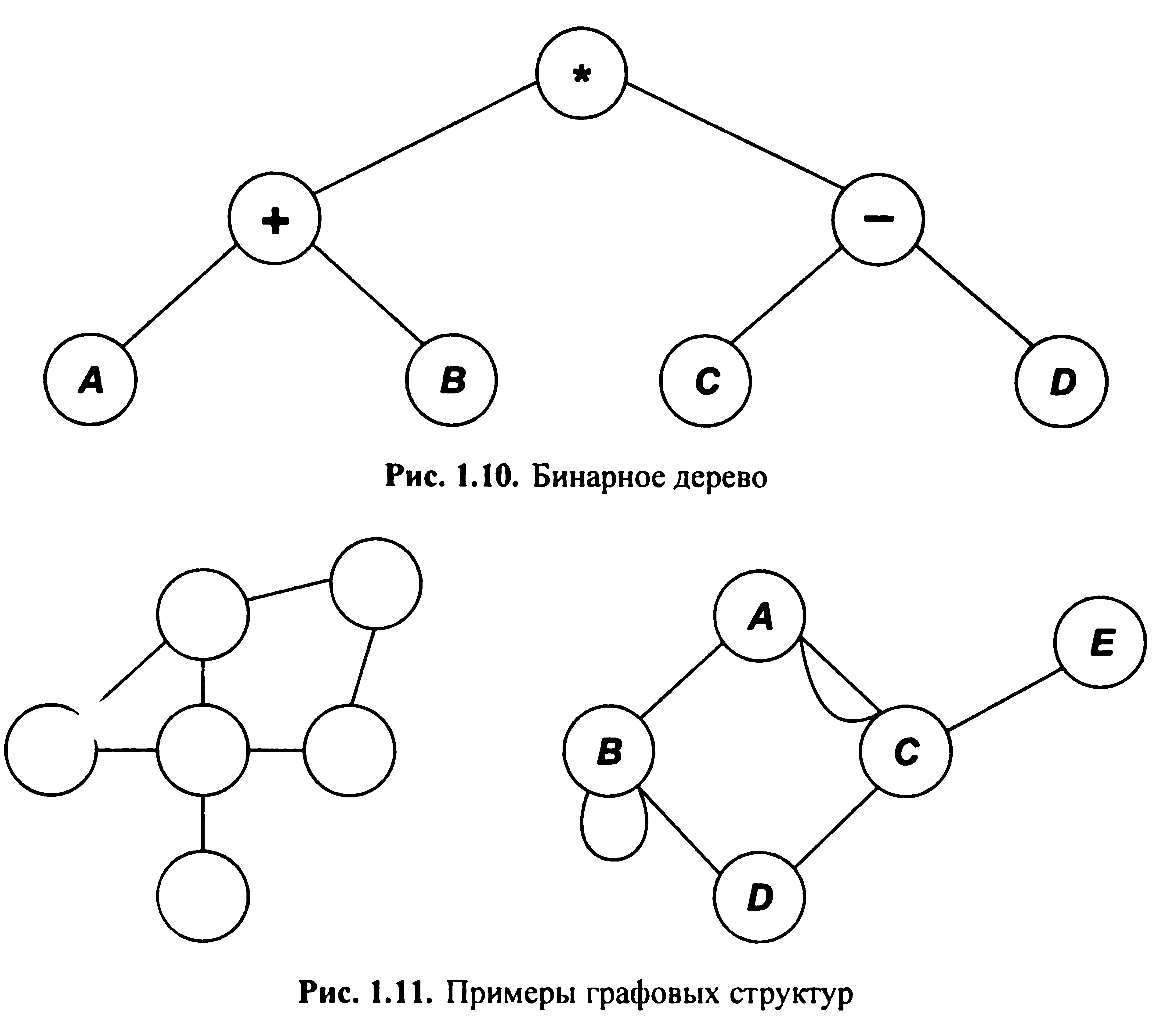
Багатозв ’ язна структура володіє наступними властивостями: 1) на кожен елемент (вузол, вершину) може бути довільна кількість посилань; 2) кожен елемент може мати зв'язок з будь-якою кількістю інших елементів; 3) кожна зв'язка (ребро, дуга) може мати напрямок і вага.

Типовими графами є схеми авіаліній і схеми метро, а на географічних картах - зображення залізних і автомобільних доріг. Вибрані точки графа називаються його вершинами, а з'єднують їх лінії-ребрами. • Сплетіння (многосвязный список, плекс) - це нелінійна структура даних, що поєднує такі поняття, як дерево, граф і списковая структура. Основна властивість сплетінь, відмінне від інших типів структур, - наявність у кожного елемента сплетення декількох полів з вказівниками на інші елементи того ж сплетення (мал. 1.12).

Рис. 1.12. Многосвязный список (сплетение)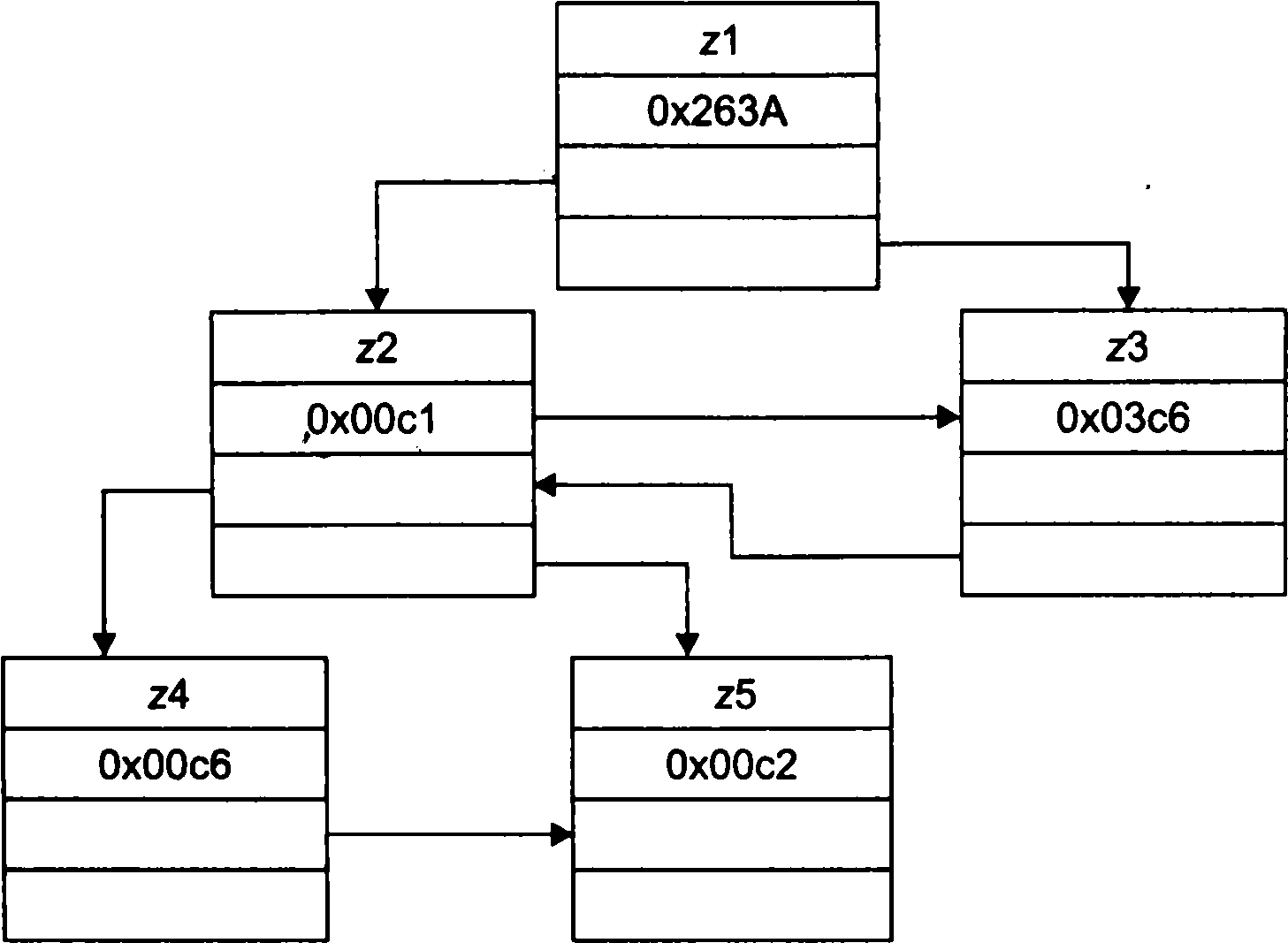

Сплетіння - зв'язок елементів, заснована на сплетінні покажчиків. Кожен елемент сплетення може містити інформацію про кількість полів з покажчиками й форматі поля даних. Плексы (сплетення) використовуються для представлення різних родин зв'язків між індивідуумами і власниками, відображають виробничі, галузеві зв'язку і т.п.

Контрольні питання

1. Що називається структурою даних? 2. Що таке логічна і фізична структура даних? 3. Чим відрізняються прості та інтегровані структури даних? 4. Назвіть основні особливості статичних, полустатических і динамічних структур. 5. Перелічіть основні типи зв'язаних списків. 6. Дайте визначення лінійних і нелінійних структур. 7. Чим відрізняються стек, черга і груд? 8. У чому полягає основна особливість ієрархічних структур? 9. Наведіть приклади графових структур.

Властивості алгоритма

Алгоритмом називається система формальних правил, чітко і однозначно визначає процес вирішення поставленого завдання у вигляді кінцевої послідовності дій або операцій. Властивості, якими повинен володіти алгоритм: 1. Кінцівку (финитность) алгоритму. Алгоритм повинен призводити до вирішення задачі обов'язково за кінцевий час. Послідовність правил, що призвела до нескінченного циклу, алгоритмом не є. 2. Визначеність, або детермінованість, алгоритму. Це властивість означає, що неоднозначність тлумачення запису алгоритму неприпустима. 3. Результативність алгоритму. Під результативністю розуміється доступність результату рішення задачі для користувача, іншими словами, алгоритм повинен забезпечити видачу результату вирішення завдання на друк, на екран монітора або у файл. 4. Масовість алгоритму. Це означає, якщо правильний результат за алгоритмом отриманий для одних вихідних даних, то правильний результат з цього ж алгоритму повинен бути отриманий і для інших вихідних даних, допустимих у даній задачі. 5. Ефективність алгоритму. Під ефективністю алгоритму буде розуміти таке його властивість (якість), що дозволяє вирішити завдання за прийнятну для розробника час. До параметру, що характеризує ефективність алгоритму, слід віднести також обсяг пам'яті комп'ютера, необхідний для вирішення завдання.

2.6.

Види алгоритмів та їх реалізація

Залежно від мети, початкових умов завдання, шляхів її вирішення, визначення дій розробника алгоритми підрозділяються на механічні, або детерміновані (жорсткі та гнучкі, або стохастичні (імовірнісні і евристичні). Механічний алгоритм задає певні дії, позначаючи їх єдиною послідовності, що забезпечує однозначний (необхідний шуканий) результат в тому випадку, якщо виконуються умови процесу, для яких розроблено алгоритм. До таких алгоритмів відносяться алгоритми роботи машин, верстатів, двигунів і т.п. Імовірнісний (стохастичний) алгоритм пропонує програму вирішення завдання декількома шляхами або способами, що призводять до досягнення результату. Евристичний алгоритм (від грецького слова «еврика») - це такий алгоритм, в якому досягнення кінцевого результату однозначно не визначено, так само як не позначена вся послідовність дій. У цих алгоритмах використовуються універсальні логічні процедури і способи прийняття рішень, засновані на аналогії, асоціаціях і минулому досвід вирішення подібних завдань. При реалізації евристичних алгоритмів велику роль відіграє інтуїція розробника. У програмуванні алгоритми поділяються на три типи: • лінійний - набір команд (вказівок), які послідовно один за одним; • розгалужується - алгоритм, що містить хоча б одну перевірку умови, в результаті якої забезпечується перехід на один з можливих варіантів вирішення; • циклічний - алгоритм, який передбачає багаторазове повторення одного і того ж дії (одних і тих же операцій) над новими вихідними даними. До циклічних алгоритмами зводиться більшість методів обчислень і перебору варіантів. Допоміжний (підлеглий) алгоритм - це алгоритм, розроблений раніше і цілком використовуваний при алгоритмізації конкретної задачі. Залежно від ступеня деталізації, поставлених цілей, методів і технічних засобів вирішення задачі використовуються різні форми подання алгоритмів. Всі варіанти подання алгоритмів можуть бути об'єднані в єдину класифікаційну схему, зображену на рис. 2.5.

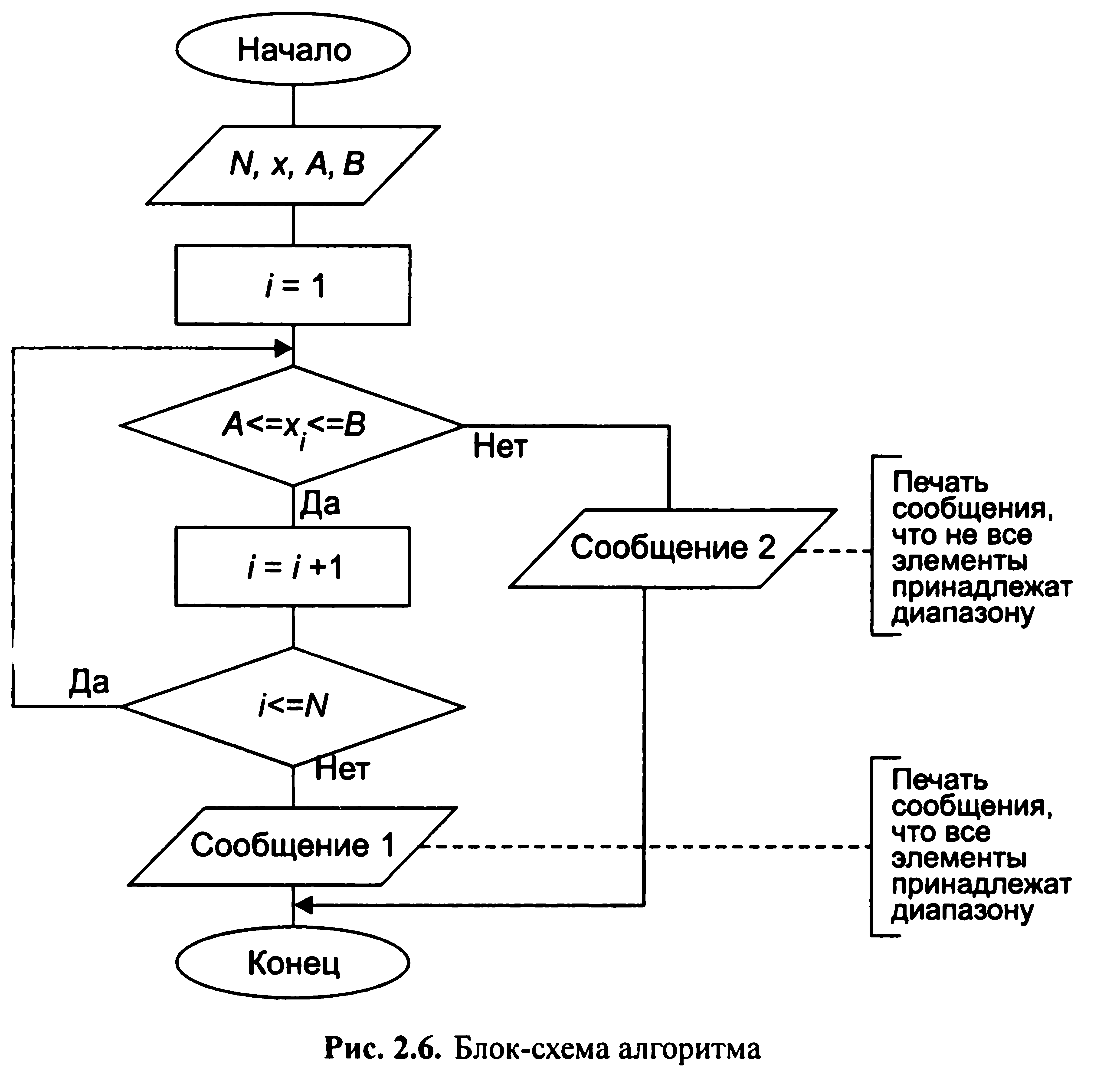
На практиці найбільш поширені наступні способи: • словесний; • формульно-словесний; • блок-схемний; • псевдокод; • структурні діаграми; • мови програмування. Словесний спосіб - зміст етапів обчислень задається на природному мовою в довільній формі з необхідної деталізацією. Наприклад, нехай задано масив чисел. Потрібно перевірити, чи всі числа належать заданому відрізку, який задається межами А та В. К р о к 1. Вибираємо перший елемент масиву - до кроку 2.

Рис. 2.5. Классификация способов представления алгоритмов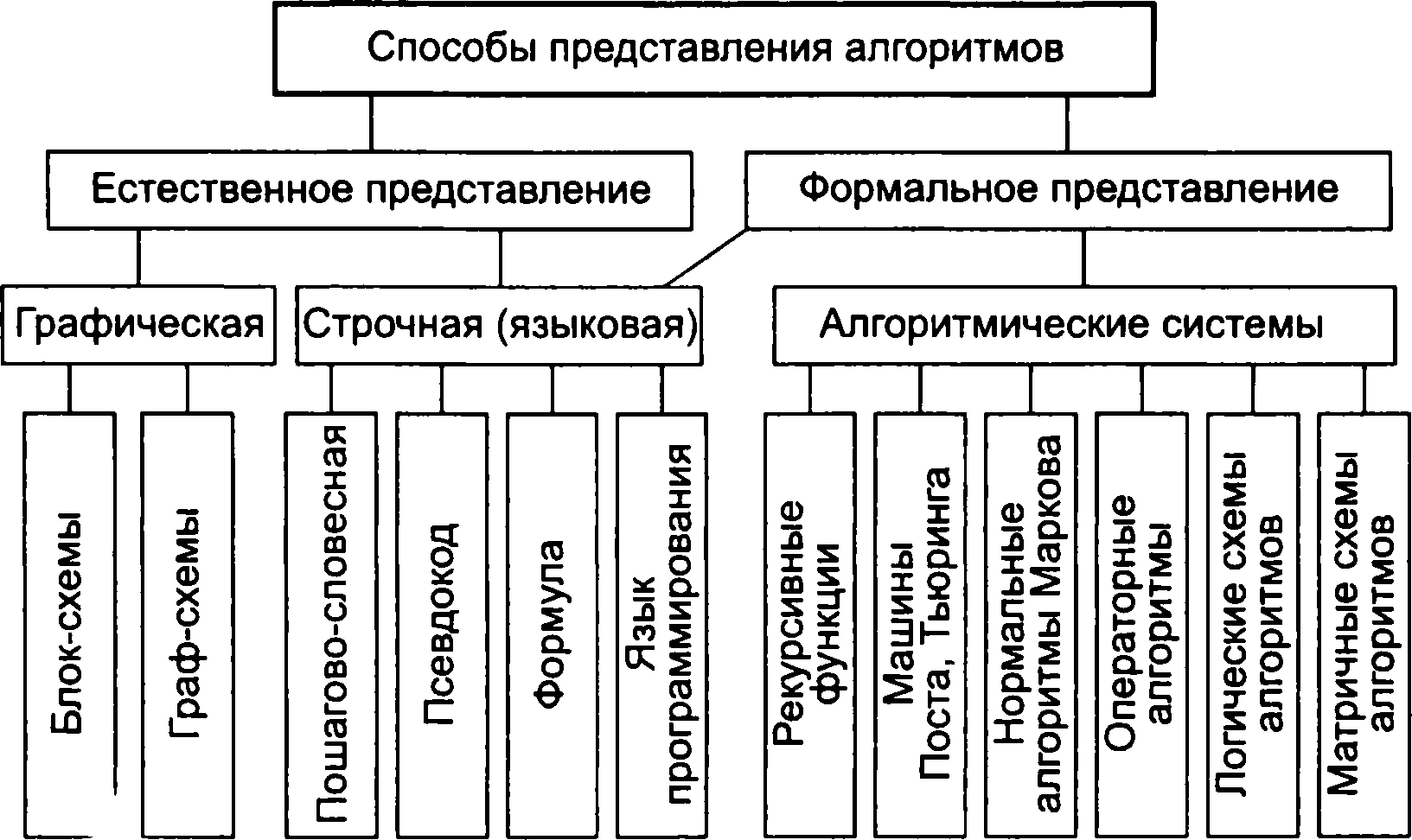

Крок 2. Порівнюємо: вибраний елемент масиву належить інтервалу - якщо «так», то до кроку 3, якщо «ні» - до кроку 6. Крок 3. Всі елементи масиву переглянуті? Якщо «так» - то до кроку 5, якщо ні - то до кроку 4. Крок 4. Вибираємо наступний елемент - до кроку 2. Крок 5. Друк повідомлення: всі елементи належать інтервалу - на крок 7. Крок 6. Друк повідомлення: не всі елементи належать інтервалу - на крок 7. Крок 7. Кінець. При цьому способі запису алгоритму відсутній наочність обчислювального процесу, так як немає достатньої формалізації. Формульно-словесний спосіб - завдання інструкцій з використанням математичних символів і виразів у поєднанні зі словесними поясненнями. Наприклад, обчислити площа трикутника по трьом сторонам а, b, с. Даний алгоритм може бути представлений наступним чином: Крок 1. Обчислити полупериметр трикутника р = (a + b + c)/2.

К рок 2. Обчислити

Крок 3. Надрукувати результат S і припинити обчислення. При використанні цього способу може бути досягнута будь-яка ступінь деталізації більш наочно, але не строго формализованно. Блок-схемний спосіб-це графічне зображення алгоритму, в якому кожен етап процесу обробки даних подається у вигляді геометричних фігур (блоків), які мають певну конфігурацію залежно від характеру виконуваних операцій. У табл. 2.1 наведені найбільш часто використовувані блоки.

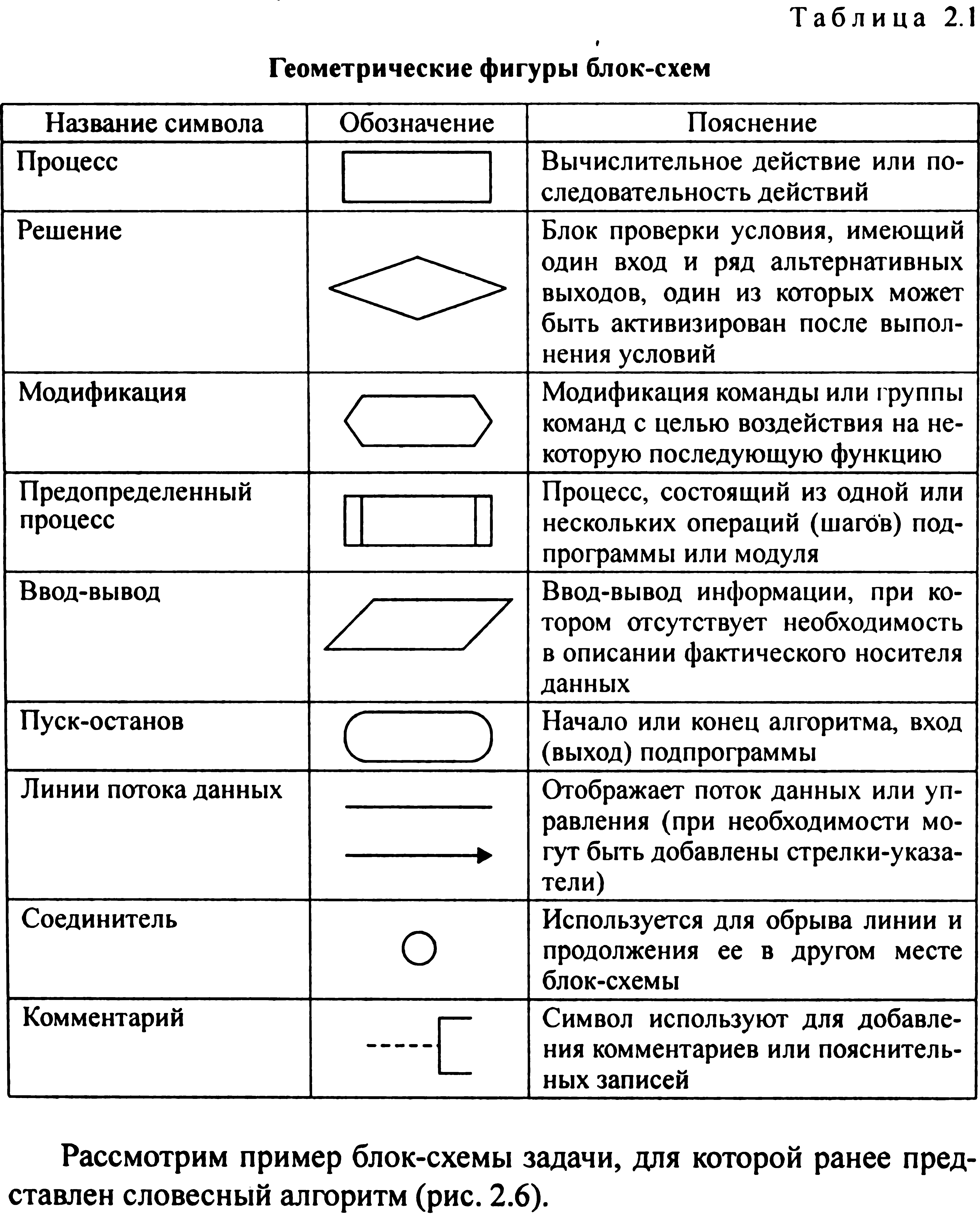
П севдокод являє собою сукупність операторів мови програмування і природної мови. Запис алгоритму у вигляді псевдокода представлена нижче:

При запису алгоритму на псевдокоде кожне окреме пропозиція може починатися з зірочки (*). Алгоритм будується таким чином, що розбиття продовжується до тих пір, поки кожен крок алгоритму не стане достатньо зрозумілим.

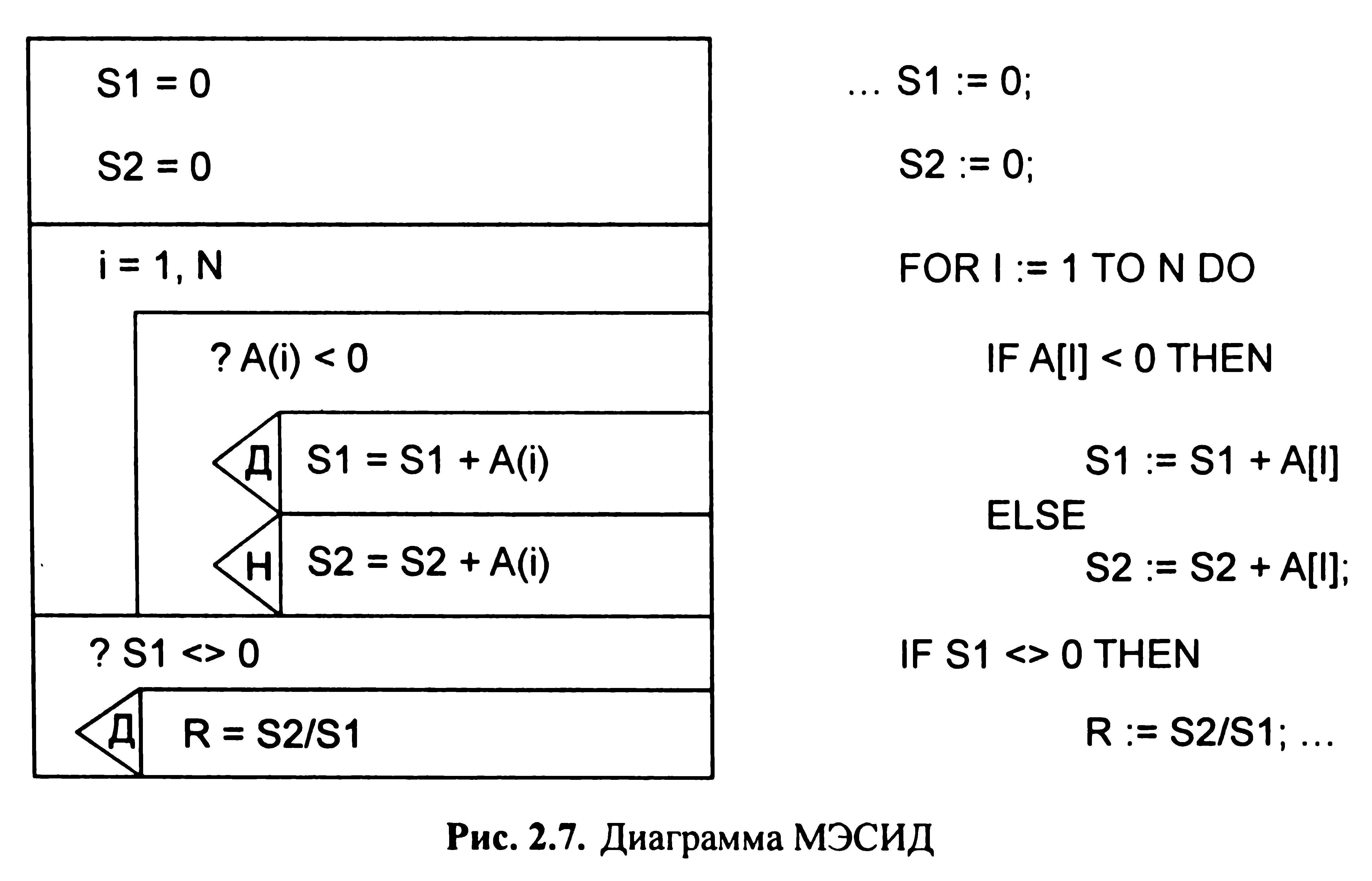
33

2.7.

Базові канонічні структури алгоритмів

Для реалізації алгоритмів на ПЕОМ використовується алгоритмічний мова - набір символів і правил освіти і ілюмінації конструкцій з цих символів для запису алгоритмів. Будь-яку програму можна написати, використовуючи комбінації трьох базових структур: • проходження, або послідовності операторів; • розгалуження, або умовного оператора; • повторення, або оператора циклу. Програма складена з канонічних структур, називається регулярній програмою, тобто має один вхід і один вихід. Оскільки алгоритм визначає порядок обробки інформації, він повинен містити, з одного боку, дії по обробці, а з іншого - порядок їх проходження, званий управління потоком. Розглянуті вище блоки, пов'язані з обробкою даних, діляться на прості та умовні. Особливість простого дії в тому, що воно має один вхід і один вихід, на відміну від умовного, що володіє двома виходами в залежності від того, істинним чи виявиться умова. Проста дія не означає, що воно єдине, - це може бути певна послідовність дій. Частина алгоритму, організована як просте дію, тобто має один вхід (виконання завжди починається з одного і того ж дії) і один вихід (тобто після завершення даного блоку завжди починає виконуватися одне і те ж дію), називається функціональним блоком. З цього визначення, зокрема, випливає, що кожне проста дія є функціональним блоком, а умовне - немає. Згідно з положеннями структурного програмування можна виділити всього три різні варіанти організації потоку управління діями алгоритму. Потік управління може володіти наступними властивостями: • кожен блок виконується не більше одного разу; • виконується кожен блок. Потік управління, в якому виконуються обидва ці властивості, називається лінійним; в ньому кілька функціональних блоків виконуються послідовно. Лінійним потоку мовою блок-схем відповідає структура, показана на мал. 2.8.

Очевидно декілька блоків, пов'язаних лінійним потоком управління, можуть бути об'єднані в один функціональний блок (мал. 2.9).

Рис. 2.9. Функциональный блок

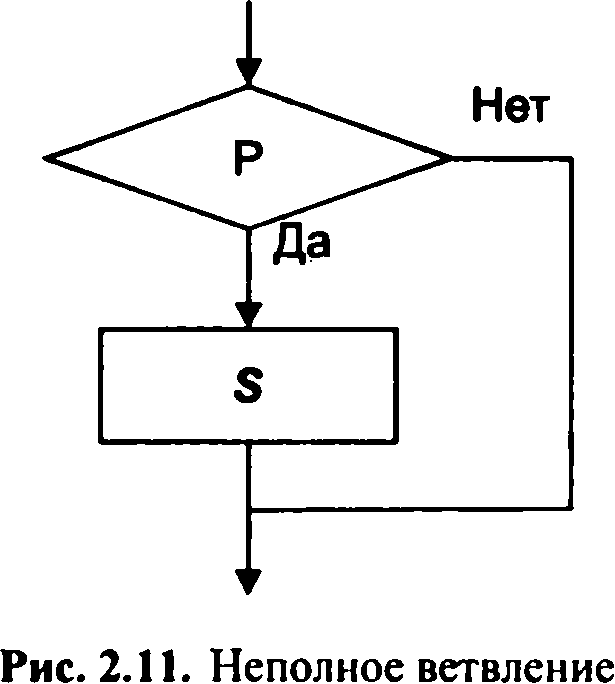
Другий тип потоку управління називається галуженням - він організовує виконання одного з двох функціональних блоків залежно від значення, що перевіряється логічного умови. Перевірка Р видається предикатом, тобто функцією, яка задає булеве або умова, величина якого може бути правда чи брехня. Якщо структура містить два функціональних блоку (5т і 52), розгалуження називається повним (мал. 2.10); можливе існування неповного розгалуження - при цьому один блок відсутній (мал. 2.11).

Рис. 2.10. Полное ветвление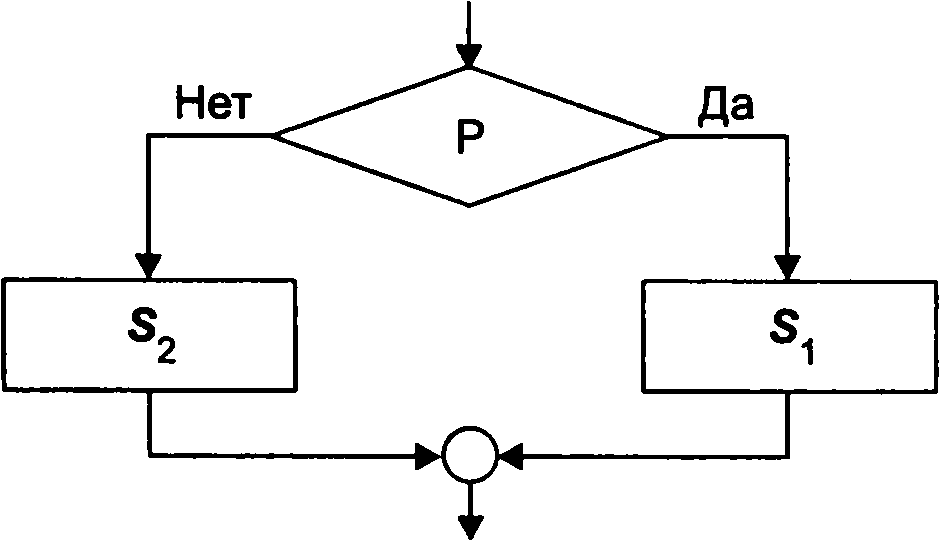

Перемикач - вибір одного варіанта з безлічі можливих альтернатив. В залежності від значення Р виконується одна з дей( зий A,B,...Z (мал. 2.12). Після вибору варіанту відбувається перехід до виконання наступного керуючої структури.

Рис. 2.12. Схема переключателя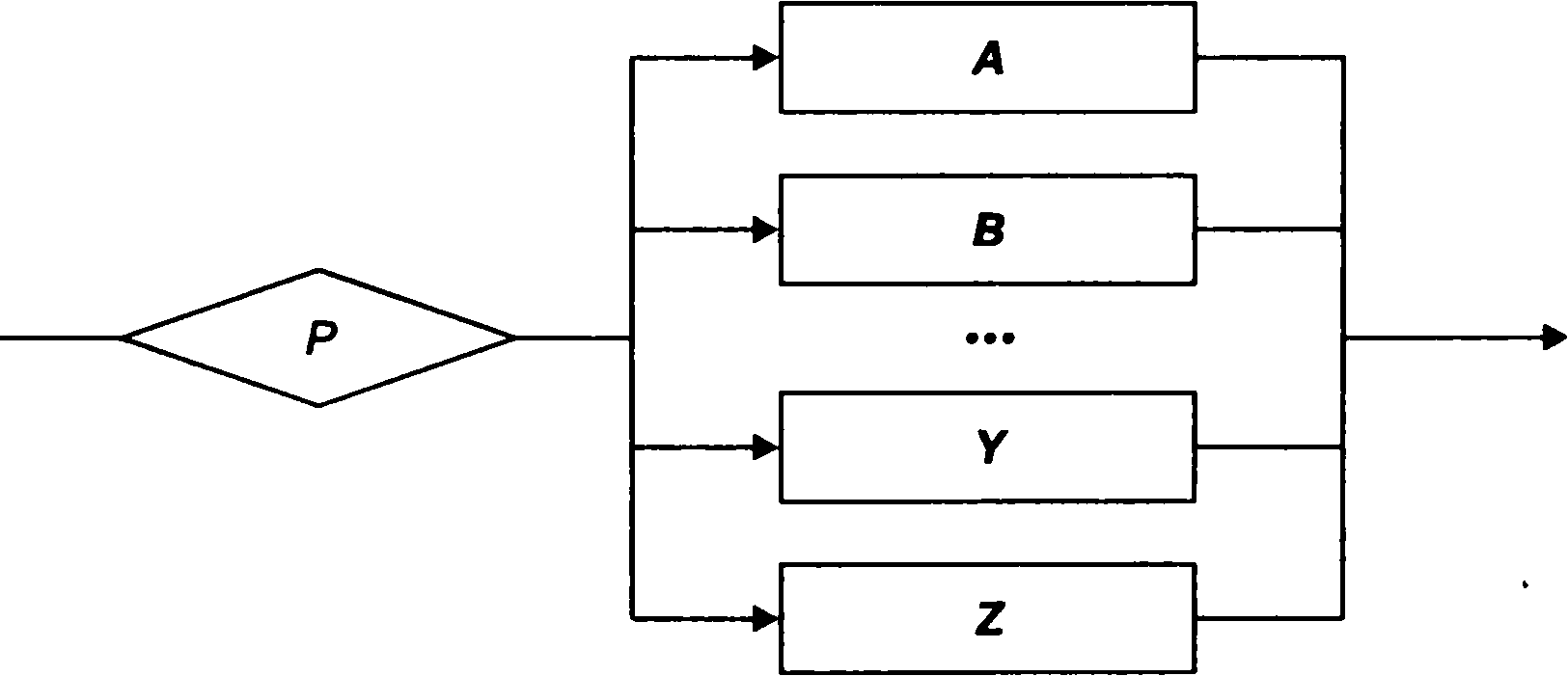

Повторення - багаторазове виконання фрагментів алгоритму (програми). Такий тип потоку управління називається циклічним - він організовує багаторазове повторення функціонального блоку, поки логічне умова його виконання є істинним. Дію А буде повторюватися до тих пір, поки значення предиката Р залишатиметься вірним (мал. 2.13). Тому в дію А повинні змінюватися значення змінних, від яких залежить Р, в іншому випадку відбудеться зациклення.

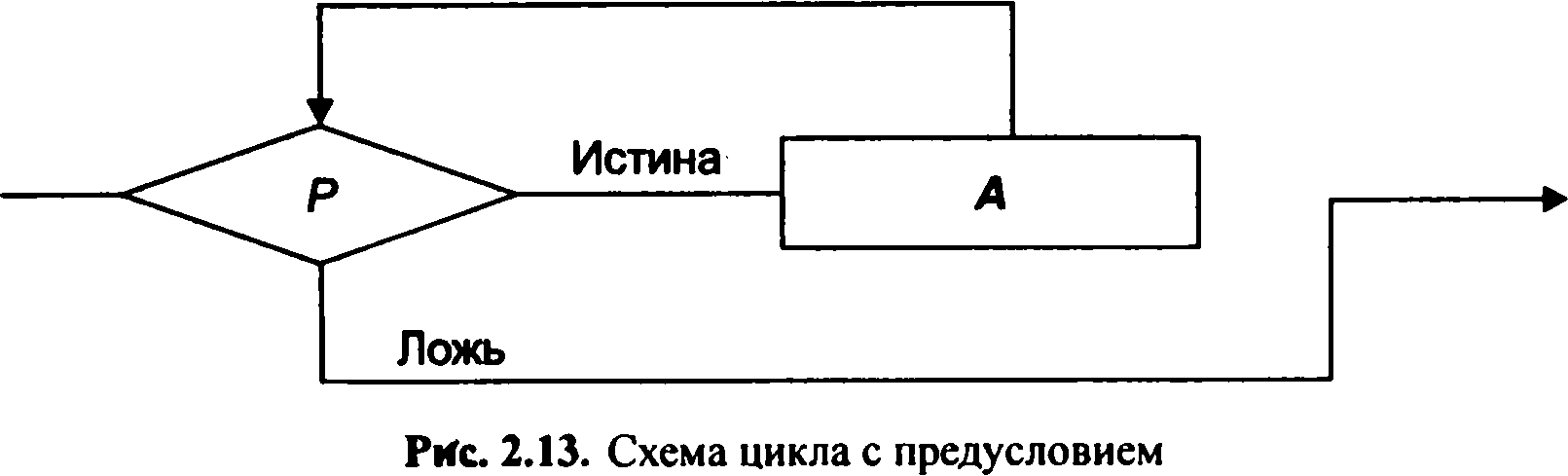
Обчислення предиката Р може проводитися після виконання дії А, в цьому випадку дія А буде виконуватися хоча б один раз (мал. 2.14).

Рис. 2.14. Схема цикла с постусловием

Алгоритм називається структурним, якщо він являє собою комбінацію з трьох розглянутих вище структур (вони називаються базовими алгоритмічними структурами). Безумовно, не всі алгоритми є структурними. Однак саме структурні алгоритми мають ряд чудових переваг порівняно з неструктурными: • зрозумілість і простота сприйняття алгоритму (оскільки невелика кількість вихідних структур, якими він утворений); • легкість перевірки (для перевірки будь-який з основних структур досить переконатися в правильності вхідних в неї функціональних блоків); • модифицируемость (вона полягає в простоті зміни структури алгоритму, оскільки складові блоки відносно незалежні). Після введених визначень можна сформулювати структурну теорему Бома - Джакопини: будь-який алгоритм може бути зведений до структурної. Іншими словами, будь-якому неструктурному алгоритму може бути побудований еквівалентний йому структурний алгоритм.

2.8.

Повна побудова алгоритма

В останні роки велике поширення отримала концепція структурного програмування. Поняття структурного програмування включає певні принципи проектування, кодування, тестування і документування програм відповідно до заздалегідь визначеної жорсткої дисципліною. Повне побудова алгоритму передбачає послідовне виконання наступних етапів: 1) постановка завдання; 2) побудова моделі; розробка алгоритму; 4) перевірка правильності алгоритму; 5) реалізація, тобто програмування алгоритму; 6) аналіз алгоритму і його складності; 7) перевірка (налагодження) програми; 8) складання документації. Не всі ці етапи чітко розрізняються між собою, особливо ця помітність робиться мало помітною при програмуванні простих завдань (мал. 2.15). При програмуванні простих завдань деякі етапи можуть взагалі не виконуватися - настільки очевидні їх результати.

Рис. 2.15. Этапы решения задач на ЭВМ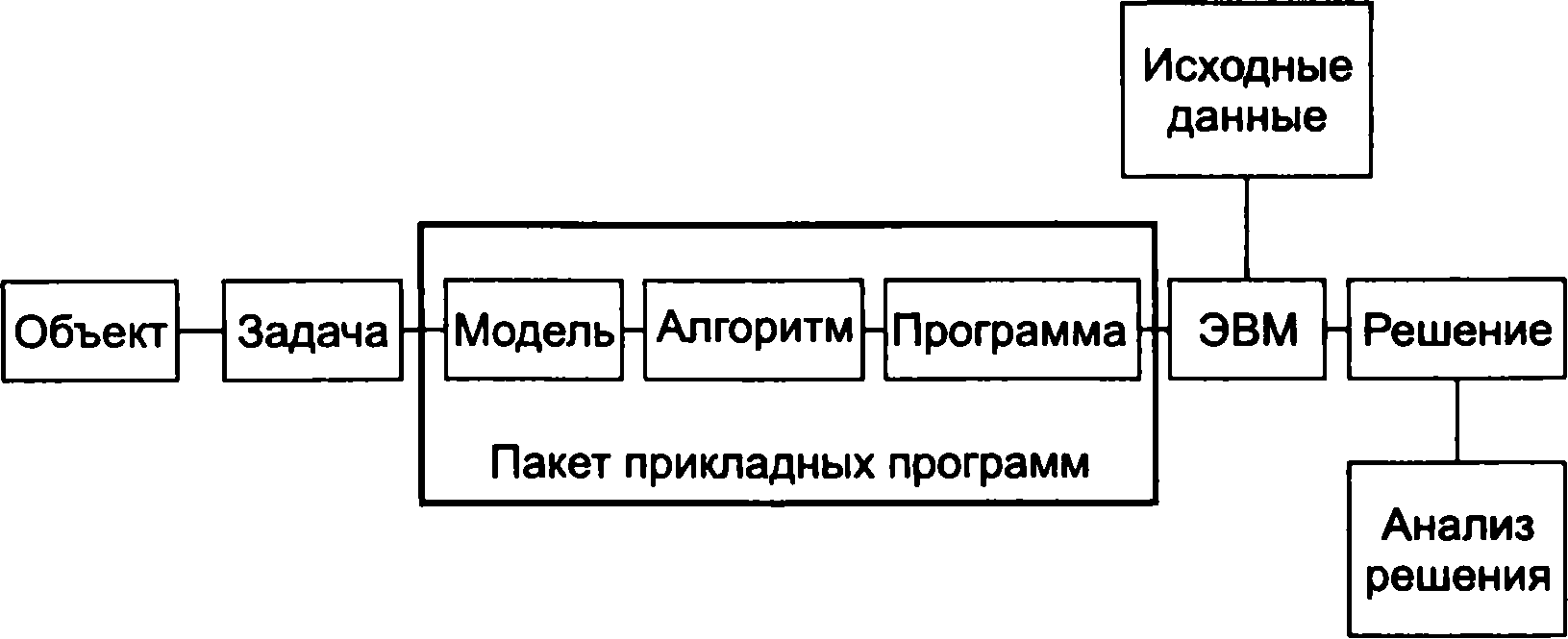

При програмуванні складних, об'ємних завдань деякі з перерахованих вище етапів доводиться виконувати не у тому порядку, як зазначено вище, або виконувати їх не один раз. Розглянемо більш докладно кожен з етапів побудови алгоритму. Постановка задачі. Перш ніж зрозуміти завдання, її потрібно точно сформулювати. Це умова саме по собі не є достатнім для розуміння завдання, але воно абсолютно необхідно. Зазвичай процес точного формулювання завдання зводиться до постановки правильних питань. Перелічимо деякі корисні питання для погано сформульованих завдань: • Чи зрозуміла термінологія, використовувана в попередньою формулювання? • Що дано? Що потрібно знайти? • Як визначити рішення? • Яких даних не вистачає або, навпаки, чи всі перелічені у формулюванні завдання дані використовуються? • Які зроблені припущення? Можливі й інші питання, що виникають в залежності від конкретної задачі. Побудова моделі. Завдання чітко поставлена, тепер треба сформулювати для неї математичну модель. Вибір моделі істотно впливає на інші етапи в процесі рішення. Вибір моделі - більшою мірою мистецтво, ніж наука. Правда, якщо ви будете зустрічатися з типової завданням, то досвід, придбаний раніше, не зажадає від вас особливого творчого підходу, і в цьому випадку буде зручно і доцільно скористатися раніше напрацьованими правилами. Тому вивчення вдалих моделей - це найкращий спосіб придбати досвід у моделюванні. Приступаючи до розробки моделі, слід вказати принаймні два основних питання: 1. Які математичні структури найбільше підходять для завдання? 2. Чи існують вирішені аналогічні завдання? Друге питання, можливо, найкорисніший у всій математики. В контексте моделювання він часто дає відповідь на перше питання. Дійсно, більшість розв'язуваних у математики завдань, як правило, є модифікаціями раніше вирішених. Спочатку потрібно розглянути перше питання. Ми повинні описати математично, що ми знаємо і що хочемо знайти. На вибір відповідної структури будуть впливати наступні фактори: • обмеженість наших знань відносно невеликою кількістю структур; • зручність подання; • простота обчислень; • корисність різних операцій, пов'язаних з розглянутої структурою або структурами.

Зробивши пробний вибір математичної структури, завдання слід переформулювати у термінах відповідних математичних об'єктів. Це буде одна з можливих моделей, якщо ми можемо ствердно відповісти на питання: • Вся важлива інформація завдання добре описано математиче - ск! і об'єктами? • Чи існує математична величина, яку асоціюють з шуканим результатом? • Виявили чи ми які-небудь корисні відносини між об'єктами моделі? • Чи можемо ми працювати з моделлю? Чи зручно працювати з нею? Розробка алгоритму. Вибір методу розробки алгоритму часто сильно залежить від вибору моделі і може значною мірою вплинути на ефективність алгоритму рішення. Два різних алгоритму можуть бути правильними, але дуже сильно відрізнятися по ефективності. Правильність алгоритму. Доказ правильності алгоритму - це один з найбільш важких, а іноді і особливо стомлюючих етапів створення алгоритму. Ймовірно, найбільш поширений прийом докази правильності програми - це прогін її на різних тестах. Якщо видані програмою відповіді можуть бути підтверджені відомими або обчисленими вручну даними, виникає спокуса зробити висновок, що програма працює правильно. Однак цей метод рідко виключає всі сумніви; може існувати випадок, в якому програма не працює. Розглянемо наступну загальну методику докази правильності алгоритму. Припустимо, що алгоритм описаний у вигляді послідовності кроків, припустимо, від кроку 0 до кроку га. Постараємося запропонувати якусь обґрунтування правомірності для кожного кроку. Зокрема, може знадобитися формулювання про затвердження умовах, що діють до і після пройденого кроку. Потім постараємося запропонувати доказ кінцівки алгоритму, при цьому будуть перевірені всі підходящі вхідні дані отримані всі відповідні вихідні дані. Інший метод докази правильності алгоритму, який не має спеціальної назви, полягає в наступному. Для кожного циклу, який є в програмі (алгоритм), вручну (наприклад, на калькуляторі) враховуються дві контрольні точки. Якщо контрольні точки збігаються зі значеннями, виданими програмою, можна бути впевненим, що всі цикли у програмі працюють правильно. Чому мова йде про двох контрольних точках? Справа в тому, що перше контрольне значення в програмі може бути обчислені правильно, а потім у цьому циклі будуть зроблені деякі некоректні дії, які призведуть до спотворення всіх подальших результатів. Збіг другого контрольного значення якраз і підтверджує, що в даному циклі некоректності немає. Таким чином, два контрольних обчислення повинні бути зроблені для кожного циклу програми.

Слід підкреслити той факт, що правильність алгоритму ще нічого не говорить про його ефективності. У цьому сенсі вичерпні алгоритми, або, як їх ще називають, алгоритми повного перебору, рідко бувають гарними у всіх відносинах. Реалізація алгоритму. Як тільки алгоритм виражений, припустимо, у вигляді послідовності кроків і ми переконалися в його правильності, настає черга реалізації алгоритму, тобто написання програми для комп'ютера. При цьому виникають такі проблеми. • Дуже часто окремо взятий крок алгоритму може бути виражений у формі, яку важко перекласти безпосередньо в конструкції мови програмування. Наприклад, один з кроків алгоритму може бути записаний у вигляді, що потребує цілої підпрограми для своєї реалізації. • Реалізація може виявитися складним процесом тому, що перед тим, як написати програму, необхідно побудувати систему структур даних для подання важливих аспектів своєї моделі. Щоб зробити це, необхідно відповісти на такі питання: Які основні змінні? Яких вони типів? Скільки потрібно масивів і який розмірності? Чи має сенс користуватися зв'язними списками? Які потрібні підпрограми (можливо, вже записані в пам'яті)? Якою мовою програмування користуватися? Конкретна реалізація може істотно впливати на вимоги до пам'яті і на швидкість алгоритму. Зауважимо, що одна справа - довести правильність конкретного алгоритму, описаного в словесній формі, інше - довести, що дак ая машинна програма, імовірно є реалізацією цього алгоритму, також правильна. Тому необхідно дуже ретельно стежити, щоб процес перетворення правильного алгоритму (у словесній формі або формі схеми алгоритму) в програму, написану алгоритмічною мовою, заслуговував довіри.