§ 2.6. Преобразования электрических цепей

Понятие об эквивалентных преобразованиях

Анализ процессов в электрических цепях во многих случаях мо­жет быть существенно упрощен за счет использования различных пре­образований, в результате которых отдельные участки идеализирован­ных цепей заменяются участками с более простой топологией или участками, более удобными для анализа.

Два участка идеализированной электрической цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Пре­образования электрических цепей, в результате которых некоторые участки электрической цепи заменяются эквивалентными им участка­ми, называются эквивалентными. Из определения эквива­лентных участков следует, что они должны иметь одинаковое коли­чество внешних выводов, причем в процессе эквивалентных преобра­зований токи этих выводов и напряжения между ними должны остг ваться неизменными.

Эквивалентные участки электрических цепей обладают свойства­ми симметричности (если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А), рефлексивности (цепь А яв­ляется эквивалентной самой себе) и т р а и з и с т и в н о с т и (если цепь А эквивалентна цепн Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными). Если эквивалентность двух участ­ков электрической цепи выполняется при любых значениях внешних воздействий, то такие участки являются полностью эквива­лент н ы м и. Различия между ними не могут быть установлены с помощью каких-либо измерений, проводимых на внешних выводах. Если эквивалентность двух участков выполняется только при опре­деленном значении внешних воздействий, то такие участки являются частично эквивалентными (эквивалентными при за­данных условиях). Так, два участка линейной электрической цепи, находящейся под гармоническим воздействием, могут быть либо полностью эквивалентными, либо частично при заданной частоте внешнего воздействия.

Эквивалентные преобразования электрических цепей основаны на эквивалентных (равносильных) преобразованиях соответствующих систем уравнений электрического равновесия. Каждое равносильное преобразование системы уравнений электрического равновесия исходной цепи (приведение подобных членов, исключение неизвестных, замена переменных и т. д.) приводит к эквивалентному преобразованию моде­лирующей цепи. Соответственно изменяется и условное графическое изображение моделирующей цепи — схема цепи. На практике пре­образования электрических цепей проводят без составления систем уравнений электрического равновесия, путем непосредственного пре­образования схем по определенным правилам. Систему уравнений электрического равновесия цепи составляют для уже преобразованной цепи, схема которой имеет достаточно простой вид.

Рассмотрим правила преобразования цепей с последовательным и параллельным соединением элементов.

Участки цепей с последовательным

соединением элементов

Рассмотрим неразветвленную электрическую цепь (рис. 2.29, а), содержащую N сопротивлений, М емкостей, К индуктивностей и v Неуправляемых источников напряжения (обобщенная Одно­контурная цепь).Так как через все элементы цепи протекает один и тот же ток i, то уравнение электрического равновесия, состав­ленное на основе второго закона Кирхгофа и компонентных уравне­ний, может быть записано в следующей форме:

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

После приведения подобных членов (2.124) принимает вид

t

+ J idt + L_3K е,,<, (2.125)

— оо

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

Уравнению (2.125) соответствует преобразованная цепь, схема ко­торой изображена на рис. 2.29, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каж­дую из групп последовательно включенных однотипных элементов за­менить одним эквивалентным элементом, параметр которого R_3K, С_эк, L_3K ^и е_Э1( рассчитывается в соответствии с (2.125).

Из выражения (2.125) следует, что при последовательном включении сопротивлений, индуктивностей и источников напряжения параметры эквивалентного элемента R_aK, L_3K и е_эк равны сумме параметров по­следовательно включенных элементов соответствующего типа. При этом суммирование э. д. с. источников напряжения производится ал­

гебраически, с учетом их знаков, которые определяются тем, совпа­дает или не совпадает направление э. д. с. с направлением обхода кон­тура. Очевидно, что R_3K и L_3K будут превышать сопротивление и ин­дуктивность любого из последовательно включенных элементов. При последовательном соединении N одинаковых сопротивлений R или индуктивностей L параметр эквивалентного элемента R_3K или L_3K бу­дет в N раз больше, чем параметр каждого из последовательно вклю­ченных элементов.

При последовательном включении емкостей значение величины, об­ратной С_эк, определяется как сумма обратных значений всех последо­вательно включенных емкостей, причем эквивалентная емкость С_эк

-II-

-эк

⁵>

j Zm

Рис 2.29. Преобразование участка цепи с последовательным соединением

элементов

U

О

^сэк

г)

~-е

-ЭН

меньше, чем любая из последовательно включенных емкостей. При последовательном включении N одинаковых емкостей эквивалентная емкость С_эк в N раз меньше каждой из последовательно включенных емкостей.

Если обобщенная одноконтурная цепь находится под гармоничес­ким воздействием, то от эквивалентной схемы для мгновенных значе­ний (рис. 2.29, а) удобнее перейти к эквивалентной схеме для комп­лексных действующих значений (рис. 2.29, в). Уравнение электричес­кого равновесия такой цепи, составленное на основании закона Ома и второго закона Кирхгофа в комплексной форме, имеет следующий вид:

Zri /+ ... -\~Zrn / + Zci / + i'ZcM / / + ...•+■

+ z_lk/=0-ie₁+...+e_v].

После преобразований получаем

(2.126)

-'эк’

z_mI=u-

V

- S E_t.

i

N М К

где Z_3K = 2 Zri + 2 Za + 2 Z_Li;

- f=i- #=i- <=i-

Комплексная схема замещения цепи, соответствующая уравнению (2.126), приведена на рис. 2.29, г.

Таким образом, любой участок электрической цепи, представляющий собой последовательное соединение произвольного количества идеализированных не­управляемых источников напряжения и идеализированных пассивных двухполюс­ников, при гармоническом воздействии может быть заменен ветвью, содержа­щей один источник напряжения, э.д.с. которого равна алгебраической сумме э.д.с. всех последовательно включенных источников, и один пассивный двухпо­люсник, комплексное сопротивление которого равно сумме комплексных сопротив­лений всех последовательно включенных пассивных двухполюсников.

Участки цепей с параллельным соединением элементов

Пусть электрическая цепь (рис. 2.30, а) состоит из параллельно соединенных N сопротивлений, М емкостей, К индуктивностей и v неуправляемых источников тока (обобщенная двухузло­вая цепь). Все элементы цепи находятся под одним и тем же на­пряжением и, поэтому уравнение электрического равновесия, состав­ленное на основании первого закона Кирхгофа, может быть записано в форме

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

где ^ = 2 дт’ ^ак 2 £<» г г.; /вк — 2 it-

^»к i I iszr.! *-ак tr~! Lt

Уравнению (2.128) соответствует преобразованная цепь, схема ко­торой приведена на рис. 2.30, б Видно, что ток и напряжение на за­жимах обобщенной двухузловой цепи не изменятся, если каждую

из групп параллельно включенных однотипных элементов заменить одним эквивалентным элементом, параметры которою #_0К, С_эк, L_0K и /ак рассчитываются в соответствии с (2.128).

Из выражения (2.128) следует, что при параллельном включении ем­костей и источников тока параметры эквивалентного элемента С_ви, /вн ровны сумме параметров параллельно включенных элементов соот­ветствующего типа. При этом суммирование токов источников тока производится алгебраически с учетом нх знаков, определяемых ориен­тацией источников относительно узла, для которого составляется уравнение (2.127). Очевидно, что С_9К превышает по значению любую из параллельно включенных емкостей С%, ..., С_м, При параллельном соединении N одинаковых емкостей С_вн — NC.

При параллельном включении сопротивлений или индуктивностей значения величин, обратных R_3K и L_3K, будут определяться как сумма обратных значений этих сопротивлений или индуктивностей. Значе­ния R_3K ^и ^эк будут меньше, чем сопротивление или индуктивность любого из параллельно включенных элементов соответствующего типа. При параллельном включении одинаковых сопротивлений R или индук­тивностей L, R_3K = R/N, a L_3K = UN.

Уж Ы Усг Уемmfu I К,кмО ^

Jv

Рис, 2 30. Преобразование участка цепи с параллельным соединением

элементов

Для рассмотрения параметров обобщенной двухузловой цепи при гармоническом воздействии воспользуемся комплексной схемой заме­щения этой цепи (рис. 2.30,в). Уравнение электрического равновесия цепи в комплексной форме может быть записано следующим образом:

/ = Уя1 U + ••• +Yrn 0 + Ус1 0 +... Уем 0 + Y_u U +... +

+ Y_LKU — [j₁~\-...+J_v] или / = Y_0KU—j_3K, (2.129)

N М К v

где Y_3K =- S Y_Rl + 2 ^yci + 2 У Ul j₃ к = 2 ^Jf

— 1=1“ 1=1 — 1=1— (= 1

Комплексная схема замещения цепи, соответствующая уравнению (2.129), изображена на рис. 2.30, г.

Таким образом, любой участок электрической цепи, представляющей собой параллельное соединение произвольного количества идеализированных пассив­ных двухполюсников, может быть заменен одним пассивным двухполюсником, комплексная проводимость которого Y_3K 0авна сумме комплексных проводимос­тей всех параллельно включенных двухполюсников. Произвольное количество па­раллельно включенных идеализированных источников тока может быть заменено одним источником, комплексное действующее значение тока которого /_эк равно сумме комплексных действующих значений токов всех параллельно включенных источников.

Переходя в (2.129) от комплексных проводимостей к комплексным сопротивлениям, найдем эквивалентное комплексное входное сопро-

тивление Z_3K группы параллельно включенных идеализированных

пассивных двухполюсников:

1 ^N 1 ^м 1 ^к I

Т--2 Т-+2 -7— <^2Л30>

£^эк г^1 _Ri гГ| ±ci

Выражения, подобные (2.129) и (2.130), можно получить для ком­плексной проводимости и комплексного сопротивления любого участ­ка цепи, являющегося параллельным соединением произвольного ко­личества идеализированных пассивных двухполюсников с заданным

комплексным входным сопротивлением Z* или комплексной входной

проводимостью YI.

~t- <^2Ш>

i= i —^эк 1

где N — число параллельно включенных двухполюсников.

Используя (2.131), найдем выражение для комплексного входного сопротивления участка цепи, представляющего собой параллельное соединение двух элементов с комплексными сопротивлениями и Z₂:

Z_3K = ZiZj/fZ, + Z_a). (2.132)

Участки цепей со смешанным

соединением элементов

Правила преобразования участков цепей с параллельным или по­следовательным соединением элементов могут быть применены и для преобразования пассивных участков цепей со смешанным соединением элементов. Преобразование таких участков, представляющих собой сочетание групп параллельно или последовательно включенных эле­ментов, обычно производят в несколько этапов, на каждом из которых группу параллельно включенных элементов заменяют одним двухпо­люсником, комплексная проводимость которого равна сумме комплекс­ных проводимостей параллельно включенных элементов, а группу по­следовательно включенных элементов — одним двухполюсником, ком­плексное сопротивление которого равно сумме комплексных сопротив­лений всех последовательно включенных элементов.

• ••••

Пример 2.8. Рассмотрим преобразование участка идеализированной цепи со смешанным соединением элементов (рис. 2.31, а), содержащего группу парал­лельно включенных элементов (Z₃, Z₄) и группу последовательно включенных эле­ментов (Z,, Z₂). Заменяя параллельно включенные элементы Z₃ и Z₄ одним эле­ментом с комплексным сопротивлением

^эк1 — £₃ Z₄/(Z₃-|-Z₄),

получим преобразованную схему цепи (рис. 2.31, б) с тремя последовательно включенными элементами; Z_x Z₂ и Z_am- Заменяя эти элементы одним с комп­лексным сопротивлением

^ЭК2 “Ь ^2 £эк! ~Z₁ -j- Zj-| Z₃Z₄/(Z3 + Z4),

а) 5)

в)

Рис. 2.31. К примеру 2.8

приходим к простейшей преобразованной схеме рассматриваемого участка цепи с одним элементом Z_3K2 (рис. 2.31, в).

• ••••

Пример 2.9. Определим эквивалентную индуктивность цепи с параметрами элементов Lj =- L_a = L₃ — L_t -= 300 мкГн, схема которой приведена на рис. 2.32.

Участок цепи с тремя параллельно включенными одинаковыми индуктивно­стями L₂ ■= L₃ = Lj, обладает эквивалентной индуктивностью, в три раза меньшей, чем каомдая из параллельно включенных индуктивностей, L_3Kl = = 100 мкГн. Этот участок включен последовательно с индуктивностью L_lt поэтому искомая эквивалентная индуктивность

^ЭК2 — "I" ^ЭК1 — 400 мкГн.

• ••••

Пример 2.10. Определим комплексное входное сопротивление участка цепи с параметрами элементов R 1,5 кОм, С_г = 40 пФ, С₂ = 10 пФ, С₃ = 50 пФ частотой внешнего воздействия f = 1,2 МГц (рис. 2.33).

Параллельно включенные емкости С₂ и С₃ могут быть заменены одной экви­валентной емкостью

C₃Ki~C₂-\-C₃ — 60 пФ.

Емкости Су и С_ЭК1, включенные последовательно, заменим одной емкостью

СЭК2 -■ ^ЭК1

/(Ci + C_3Ki) — 24 пФ.

Получаем преобразованную цепь (рис. 2.33, б). В результате комплексное входное сопротивление цепи на частоте f — 1,2 МГц

Z- R—jI(2я/С_Эц<з) — 1,5 /5,53 , кОм.

Из рассмотренных примеров следует, что в результате объедине­ния групп последовательно и параллельно включенных элементов про­исходит постепенное «сворачивание» цепи, причем участок со смеишн-

R

Рис. 2.32. К примеру 2.9

R

С, ^С2 ^CJ

О

О ft

а)

Рис. 2.33. К примеру 2.10

ным соединением пассивных элементов, имеющий два внешних вывода (пассивный двухполюсник), в конечном счете, может быть заменен од­ним элементом, комплексное сопротивление которого равно входному со­противлению исходного участка цепи.

К цепям со смешанным соединением элементов относятся цепные или лестничные цепи, входное сопротивление или входная проводимость которых могут быть представлены в виде цепной

(непрерывной) дроби, т. е. с помощью выражения типа

, 1 аН

I —2

1

a_N

Рис. 2.34. Схема простейшей лестничной цепи

Коэффициенты а_ъ а_г, ..., ам называют­ся элементами цепной дроби. Число элементов дроби N может быть ко­нечным (конечная цепная дробь) или бес­конечным (бесконечная цепная дробь). Рассмотрим простейшую лестничную цепь (рис. 2.34). Нетрудно ус­тановить, что входное сопротивление этой цепи

Z=Z_r

■Zi

z₂+z₃

1

1/Z₂+1/Z₃

Заменяя в этом выражении сопротивление элемента Z₂ его проводи­мостью Y2 — 1/Z₂, получаем окончательно

Z=ZH ! .

- - Yt+UZ,

Таким образом, входное сопротивление рассматриваемой цепи мо­жет быть представлено в виде конечной цепной дроби, элементы кото­рой а_ъ а₂, а₃ равны соответственно Z_b Y_г, Z₃. Используя аналогичные преобразования, можно представить в виде цепной дроби и входное со­противление лестничной цепи более общего вида (рис. 2.35, а):

Z = Zi+ L. . (2.133)

“ ^Y_N__l+l/Z_N

Таким образом, число элементов цепной дроби равно числу идеали­зированных двухполюсных элементов, образующих лестничную цепь, причем элементами цепной дроби являются комплексные сопротивле­ния двухполюсников, образующих продольные ветви лестничной цепи (Z₁₍ Z₃,..., Z_N), и комплексные проводимости двухполюсников, входя­щих в поперечные ветви (К₂₎ У4,..., Клг-i).

а) 5)

Рис. 2.35. Схемы лестничных цепей общего вида

Если лестничная цепь содержит поперечную ветвь, подключен­ную непосредственно к внешним зажимам цепи (рис. 2.35, б), то в виде цепной дроби может быть представлена входная проводимость

У = У_г + ¹— . (2.134)

^3+ . • • +

- ^ Y_N__l + \/z_N

Таким образом, для того чтобы выражения для входных сопротив­лений или входных проводимостей лестничных цепей могли быть за­писаны в виде цепных дробей типа (2.133), (2.134), необходимо элемен­ты, образующие продольные ветви, представить их комплексными со­противлениями, а элементы, входящие в поперечные ветви, — их комплексными проводимостями.

Эквивалентное преобразование треугольника

сопротивлений в звезду и обратное преобразование

Найдем условия эквивалентности двух участков электрической це­пи (рис. 2.36, а, б), которые представляют собой соединение пассивных идеализированных двухполюсников треугольником и звездой. По опре­делению, эти участки цепи эквивалентны, если при замене одного уча­стка другим токи выводов 1_г, /_а, /з и напряжения между выводами ^12. ^23. <>31 останутся неизменными. Учитывая, что из трех напря­жений между выводами только два являются независимыми (третье может быть найдено из уравнения баланса напряжений), для экви-

Рнс. 2.36. Эквивалентные преобразования треугольник—звезда и звезда—треугольник

валентности треугольника сопротивлений звезде достаточно потребо­вать, чтобы любая пара из трех напряжений между выводами одной цепи была равна соответствующей паре напряжений другой цепи (при одинаковых значениях токов внешних выводов).

Выразим токи сопротивлений Z₁₂, Z₂₃, Z₃j, образующих стороны треугольника сопротивлений, через токи внешних выводов /_ь /₂, /₃. Составляя на основании законов Кирхгофа систему уравнений электрического равновесия этого участка цепи

2 ^12 ^23 —0> Z₁₂ 112 + Z₂₃ /₂₃ + Z₃₁ /₃₁ —0

и решая ее относительно токов /_1а, /_аз, /₃₁, находим

Лз ~(Zp 2_3i /з)/(^_г2 + ^₃ + Z₃₁); (2.135)

Используя выражения (2.135), определим напряжения между внешними выводами треугольника сопротивлений

Соответствующие напряжения между внешними выводами звезды

(рис. 2.36, б) U12 — Zj/i — Zj%, U23 — Z2/2 — Zj₃.

Приравнивая напряжения U₁₂ и i/₂₃ между внешними выводами рассматриваемых участков цепи, находим

Л

^12 1 '^23 /._l2-l-Z₂3-f-'Z3₁

(2.136)

В соответствии со сказанным равенства (2.136) должны выполнять­ся при любых значениях токов внешних выводов. Полагая в (2.136) сна­чала /.₂ = 0, а затем /₃ = 0, определяем соотношения между сопротив­лениями, при которых рассматриваемые участки цепей (рис. 2.36, а, б) будут эквивалентными:

Рассчитав сопротивления Z_lt Z₂, Z₃ по заданным Z₁₂, Z_a3, Z₃₁, можно

осуществить эквивалентную замену треугольника сопротивлений звез­дой (преобразование треугольник — звезда). Из рис. 2.36 видно, что

при этом преобразовании из цепи устраняется контур, образуемый со­противлениями Z_I2, Z₂₃, Z₃₁, и появляется новый узел — место соеди­нения сопротивлений Z_1; Z₂, Z₃.

Решая систему уравнений (2.137) относительно Z_Ia, Z₂₃, Z₃₁, полу­чим соотношения, позволяющие производить эквивалентную замену звезды сопротивлений треугольником (преобразование звезда—тре­угольник):

Z_I2 — Zy + Z₂ -Ь Z_x Z₂/Z₃;

Z23 ⁼ Z2 + Z₃ +Z₂ Z_a/Zi, (2.138)

Z31 = Z₃ -f- Z_x -J- Z₃ Zj/Z₂.

Преобразование звезда-треугольник приводит к уменьшению числа узлов преобразуемой цепи (за счет устранения узла, являющегося мес­том соединения сопротивлений Z_x, Z₂, Z₃), однако при этом появляется новый контур, образуемый сопротивлениями Z₁₂, Z₂₃, Z_3I.

Заменим в выражениях (2.138) комплексные сопротивления элемен­тов их проводимостями. Проведя преобразования, установим, что вы­ражения для комплексных проводимостей элементов, образующих стороны треугольника

Yn = Y_tYAYi + Yj+Y,y, (2.139)

^1=^#,+^- УзЬ

имеют такую же структуру, как и выражения для комплексных сопро­тивлений,.входящих в лучи звезды (2.137). Подобным образом можно получить выражения для комплексных проводимостей лучей звезды Уь Y₂, которые оказываются аналогичными выражениям для ком­

плексных сопротивлений сторон треугольника (2.138). Учитывая, что рассматриваемые участки обладают дуальными графами (рис. 2.36, в), приходим к заключению, что эти участки цепей являются дуальными.

Выражения (2. 139) могут быть обобщены и для преобразования N-лучевой звезды (см. рис. 1.23, б) в /V-угольник (см. рис. 1.23, а):

Yu^Yk Wi + U... + Ы

Здесь Y_hi — проводимость стороны /V-угольника, соединяющей узлы к и /; Y!, У₂,..., Y_n—’Проводимость элементов, образующих лучи звезды.

Обратное преобразование полного N-угольника в N-лучевую звезду в общем случае невозможно.

Применение преобразований треугольник—звезда и звезда—тре­угольник в ряде случаев позволяет существенно упростить анализ цепей, в частности иногда с помощью этих преобразований удается приводить сложные участки цепей к более простым (параллельное, последовательное или смешанное соединение элементов).

• ••••

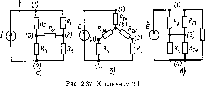
Пример 2.11. Для цепи с параметрами элементов Rj — 20 Ом, R₂ “ =--- 50 Ом, Rз 30 Ом, R_t == 25 Ом, R_b -- 30 Ом; Ё -- 1,3 В (рис 2.37, а) оп­ределим ток ветви, содержагцей источник напряжения Ё.

Ток I можно найти, решая основную систему уравнений электрического равновесия цепи, однако этот путь весьма трудоемок. Учитывая, что по условию задачи требуется определить только ток независимого источника Ё, целесообраз­но остальную часть цепи, к которой подключен этот источник, заменить комп­лексным входным сопротивлением. Непосредственное нахождение входного сопро­тивления пассивного двухполюсника, к которому подключен идеальный источник напряжения, постепенным «сворачиванием» по правилам преобразования участков

цепей с параллельным и последовательным соединением элементов невозможно, так как в данном двухполюснике отсутствуют последовательно или параллель­но включенные элементы. \

Заменим треугольник сопротивлений R_t, R₂, R₃ звездой сопротивлений R,₀, Rio (рис. 2.37, б). Используя формулы (2.137), находим:

Rio RiR3^(Ri + R% + R3) ~ 6 Ом;

R*о = R₁R-AR₁ + R₂ 4 R3) - Ю Ом;

Я зо ~ RzR 3/(^1 R2 ^ ^ з) ~ ^ Ом.

Преобразуя полученную цепь с помощью правил преобразования участков це­пей со смешанным соединением элементов, определяем входное сопротивление пас­сивного двухполюсника R — 26 Ом и искомый ток I 50 мА.

Тот же результат может быть получен, если использовать преобразование звезда—треугольник. В частности, заменяя сопротивления R_lt R₂, R*, (рис. 2.37, а) сопротивлениями

Ris = Ri 4 R2+ RtRz'Ri = Ю3,3 Ом:

R_lt — Rj •(- Ri + R₁Ri/R₂ = 62 Ом,

R34 ⁼ R₂ R& R₂Ri/Ri — 155 Ом,

получаем цепь (рис. 2.37, в), которая легко поддается дальнейшим преобразова­

ниям.

Последовательная и параллельная схемы замещения пассивного двухполюсника

Два различных линейных пассивных двухполюсника с одинаковыми комплексными сопротивлениями (комплексными проводимостями) эк­вивалентны, так как при замене одного из них другим токи и напряже­ния внешних выводов, соединяющих двухполюсники с остальной ча-

стью цепи, не изменяются. Следовательно, условием эквивалентности линейных пассивных двухполюсников является равенство их комплекс­ных сопротивлений (проводимостей).

Комплексное сопротивление любого пассивного двухполюсника Z = г + jx можно представить как сумму комплексных сопротивле­ний двух последовательно включенных двухполюсников, одно из кото­рых имеет чисто резистивный Z* = г, а другое Z_p = jx-— чисто реактивный харак­тер. Комплексную проводимость этого двухполюсника Y = 1/Z = g + jb можно рассматривать как комплексную проводи­мость цепи из двух параллельно соединен­ных элементов с проводимостями Y_a — g и F_p — jb. Поэтому, произвольному линей­ному пассивному двухполюснику, находя­щемуся под гармоническим воздействием, можно поставить в соответствие две схе­мы замещения — последовательную (рис.

2.38, а) и параллельную (рис. 2.39, а), причем каждая из них содержит один реак­тивный элемент и один элемент, входное сопротивление которого имеет чисто рези­стивный характер.

В общем случае вещественные г, g и мнимые х, b составляющие комплексного входного сопротивления и комплексной входной проводи­мости двухполюсника являются сложными функциями частоты: г ~ = г (со), х — х (со), g = g (со), b - b (ю). При изменении частоты г и g могут изменяться только по значению, а х и b — как по значению, так и по знаку.

I

\\ⁿnoc

'two

\W* =T^C

^jnoo

^jnoc

a) S)

Рис. 2.38. Последовательные схемы замещения пассивно­го двухполюсника

1

1

=±=с,

^тпар

пар

'пар

пар

Г

S)

В)

^а)

Рис. 2.39. Параллельные схемы замещения пассивного двухпо­люсника

При фиксированном значении угловой частоты со — со_х, вещественные и мнимые составляющие входных сопротивления и проводимости двух­полюсника, а следовательно, Z_a, Z_p> а также Y_а, У_р элементов последо­вательной и параллельной схем замещения принимают определенные значения Z_a = г (coj), Z_p=-jx (ш,), У_а =■ g (coj, Y_p^jb К),

Постоянное вещественное число Z_a = г (<й_х) можно рассматривать как комплексное сопротивление идеализированного пассивного эле­мента — сопротивления, входящего в последовательную схему заме­щения двухполюсника (см. рис. 2.38, б, в):

Ruoo = r(a₁). (2.140)

Мнимое число Z_p = jx (ah) в зависимости от знака х (<й_х) можно рассматривать либо как комплексное сопротивление емкости (л: (ю^с <0)

Спос =— l/toiiJC («!)], (2.141)

либо как комплексное сопротивление индуктивности (x ((Oj) ;> 0)

^пос = х K)/wi, (2.142)

входящих в эту же схему замещения.

Параллельная схема замещения двухполюсника (рис. 2.39, б, в) содержит сопротивление

Я пар = l/g(<o0 (2.143)

и либо емкость (Ь (й)_х) > 0)

Спар = Ь (сйх)/®!, (2.144)

либо индуктивность (Ь ((Di) < 0)

^пар = — 1 /[(1)₁^?((1)₁)1. (2.145)

В частном случае, когда входное сопротивление двухполюсника имеет чисто резистивный или чисто реактивный характер, обе схемы замещения вырождаются в одну схему, содержащую единственный иде­ализированный пассивный элемент (сопротивление, емкость или индук­тивность).

Таким образом, при фиксированном значении частоты внешнего воз­действия каждому линейному пассивному двухполюснику независимо от числа входящих в него элементов и способа их соединения можно поста­вить в соответствие эквивалентную схему, содержащую не более двух идеализированных пассивных элементов Разумеется, такое преобразо­вание будет эквивалентным только при ю — Wj. Изменение частоты внешнего воздействия может вызывать изменение не только значений параметров элементов последовательной и параллельной схем замеще­ния двухполюсника, но и характера соответствующих реактивных элементов.

Последовательная и параллельная цепи, схемы которых приведены на рис. 2.38, а и 2.39, а, обладают одинаковыми комплексными сопро­тивлениями (проводимостями) и поэтому являются эквивалентными. Выбор той или иной цепи и соответственно той или иной схемы замеще­ния двухполюсника при заданной частоте внешнего воздействия произ­водится только исходя из удобства последующего анализа.

При необходимости последовательная и параллельная схемы заме­щения двухполюсника могут быть преобразованы одна в другую Со­отношения между параметрами их элементов однозначно устанавлива­ются с помощью выражений (2.52) — (2.55) и (2.140)— (2.145). Ана-

Таблица 2.1. Формулы для взаимного преобразования параллельной н последовательной схем замещения пассивного двухполюсника

Параметры исходной цепи

Параметры преобразованной цепи

#пар — R пос [ 1 + 1 / (fc>i R пос^пос)²] ^пар = С_пос/[ 1 -)- ((Oj

^ПОС Япос)²]

Rn&p — R пос

^пос

Lnno.

[ 1 -f- (СО! L_noc//?noc)^s] ^■nap ⁼⁼ ^пос {1 + I^noc/(^wi ^-пос)]²}

Япар

^пар

Кпос — /?пар/[1 + (tt>! С_пар /?_пар)²] С]юс ⁼ ^пар [ 1 -)- 1 /(^ш1 Qiap ^пар)²]

Япар

^ПОС ^

-пар

пар

?пар \²1

l ^-пар J J /Г /®1 ^пар \ ²1

/.^,+Ь=Г

лиз этих выражений показывает, что при взаимных преобразованиях последовательной и параллельной схем характер реактивного элемен­та, входящего в схему замещения, не изменяется (табл. 2.1).

Выражения, приведенные в таблице, можно использовать для вза­имных преобразований произвольных участков цепей с параллельным и последовательным включением элементов. Например, при заданной частоте внешнего воздействия ш ■= <й_х участок цепи, представляющий собой последовательное соединение сопротивления R_x и емкости C_lt может быть заменен эквивалентным участком цепи с параллельно вклю­ченными сопротивлением R₂ и емкость С₂. Несмотря на то что в дан­ном случае параметры элементов исходной цепи не являются функция­ми частоты, параметры элементов преобразованной цепи R₂, С₂ зависят от частоты внешнего воздействия. При этом изменение частоты внешне­го воздействия приводит только к изменению параметров элементов преобразованной цепи; изменения характера реактивных элементов в данном случае не происходит.

• ••••

Пример 2.12. Найдем последовательную и параллельную схемы замещения последовательной RLC-цепи (см. пример 2.4) при частоте внешнего воздействия <£> — щ — 2,5- 10^е рад/с.

Комплексное сопротивление цепи при (0=0)! имеет резистивно-емкостной характер

_Z = г (о>₁) 4 jx (CjDj) = 100 — /600, Ом,

поэтому последовательная и параллельная схемы замещения цепи на данной ча­стоте содержат сопротивление и емкость (см. рис. 2.38, б, 2.39, б). Парамет­ры элементов последовательной схемы замещения в соответствии с выражениями (2.140), (2.141)

г

I

Киос, = г (o>i) — 100 Ом; С_ПОс= — 1/[% х (o>i)] = 666,7 пФ.

Параметры элементов параллельной схемы замещения найдем, используя формулы, приведенные в табл. 2.1:

R пар = R пос

[1 1 /(&>, R_lwc С,юс)²] — 3,7 кОм;

Сцар — Сц_0(;/[ 1 4" (<<Н Rnoc ^пос)²]⁼ 649 пФ.

Комплексные схемы замещения источников энергии

1

V

О*

5)

о)

Ранее были рассмотрены последовательная и параллельная схемы замещения линеаризованных источников посто­янного тока и напряжения (см. рис. 1.16, б, в) и по­лучены соотношения для их взаимного преобразования (1.35), (1.36). Покажем, что аналогичные соотношения выполняются и для линеа­ризованных источников гармонических то­ков и напряжений, т. е. для источников, комплексные схемы замеще­ния которых содержат идеальный источ­ник напряжения Ё и комплексное внут­реннее сопротивление Z_t (рис. 2.40, а) или идеальный источник тока J и ком­плексную внутреннюю проводимость Y_t (рис. 2.40, б).

Рис.. 2.40. Последовательная (а) и параллельная (б) комп­лексные схемы замещения ис­точников энергии

В соответствии с последовательной схемой замещения (рис. 2.40, а) ком­плексное действующее значение напря­жения на зажимах линеаризованного источника

U = B~Zit. (2.146)

В то же время из параллельной схемы замещения (рис. 2.40, б) получаем

(J ^ -j/Y_t-l/Y_t. (2.147)

Сравнивая выражения (2.146) и (2.147), находим условия эквива­лентности последовательной и параллельной комплексных схем за­мещения линеаризованного источника гармонических токов и напря­жений:

Ё ~J/Y_h Z,- 1/У,. (2.148)

Действительно, выражения (2.148) подобны (1.35), (1.36) и могут быть получены из последних путем замены вещественных внутреннего сопротивления и внутренней проводимости G, соответственно ком­плексным сопротивлением Z; и комплексной проводимостью Yj, а мгновенных значений тока / (t) и ч.д.с. е (t) их комплексными изображе­ниями. Как отмечалось ранее, взаимные преобразования параллельной и последовательной схем замещения возможны только для линеаризо­ванных источников с конечными внутренним сопротивлением и внут­ренней проводимостью (Zj Ф О, У₍ Ф 0).

В ряде случаев при анализе цепей возникает необходимость преоб­разовывать источники, т. е. заменять идеализированный источник одно­го типа другим. Для линеаризованных источников с конечным внут­ренним сопротивлением (проводимостью) эта задача решается путем преобразования последовательной схемы замещения источника в парал­лельную или обратно с помощью выражений (2.148). Если в экви­валентной схеме реального источника содержится только идеальный источник напряжения, однако в пепи, внешней по отношению к нему, имеется произвольный пассивный двухполюсник, включенный последо­вательно с источником, то его комплексное сопротивление Z можно рас­сматривать как внутреннее сопротивление линеаризованного источника Z;, что дает возможность воспользоваться для преобразования источ­ника выражениями (2.148). Аналогично, если параллельно идеально­му источнику тока включена любая ветвь, составленная из пассивных элементов, то ее комплексную проводимостьIYJ можно рассматривать как внутреннюю проводимость линеаризованного источника Y_t. Иде­альные источники тока и напряжения, которые могут быть преобразо­ваны один в другой таким образом, называются невырожден­ными.

Формулами (2.148) можно воспользоваться и для взаимного пре­образования невырожденных управляемых источников тока и напря­жения. Разумеется, при этом характер управляющего воздействия (ток или напряжение) не изменяется.

Если в анализируемую цепь включены идеальный источник напря­жения и последовательно с ним нет элементов, сопротивление которых можно рассматривать как внутреннее сопротивление линеаризованного источника, или идеальный источник тока, параллельно которому нет ветвей, проводимость которых можно трактовать как внутреннюю про­водимость соответствующего источника, то такие источники называют вырожденными. Вырожденные источники напряжения и тока не могут быть преобразованы один в другой непосредственно с по­мощью выражений (2.148), однако они могут быть устранены из рас­сматриваемой цепи с помощью преобразований, получивших название переноса источников.

Перенос источников

Рассмотрим участок идеализированной электрической цепи, содер­жащий вырожденный источник напряжения (рис. 2.41, а). Покажем, что данный участок цепи может быть заменен одним из эквивалентных ему участков цепей, не содержащим вырожденных источников.

Идеальный источник напряжения Ё из ветви, подключенной между узлами (6) и (7) (рис. 2.41, а), перенесем во все ветви, подключенные к узлу (6) (рис. 2.41, б) или во все ветви, подключенные к узлу (7) (рис. 2.41, в). В обоих случаях перенос источника напряжения произведен без изменения э.д.с. источника и его ориентации относительно направ­лений обхода контуров 1 и 4. Ветвь, ранее содержавшая источник Ё,

а) 5) ' В)

Рис. 2.41. Перенос идеализированного источника напряжения

после преобразования исчезает, причем узлы (6) и (7), к которым она была подключена, объединяются в один узел.

Процессы во всех трех идеализированных цепях описываются реше­ниями одной и той же системы уравнений электрического равновесия, составленной на основании законов Кирхгофа:

А + ^2 + /з^_Ь^4~Ь^5^=;0; — Z_s i_a^JrZ_it_i^J_rU_ai = 0',

—/1+Z2/2+^12—z₄ /4 ^-\~z_b

Z₂/₂ -f- Z3/3 U= Ё', Z5/5 -[- Zj/j U_&i — Ё.

Следовательно, при замене цепи (рис. 2.41, а) любой из цепей (рис. 2.41, б, в) токи внешних выводов и напряжения между ними не изменяются, т. е. участки этих цепей эквивалентны. В результате пере­носа источника вырожденный источник напряжения заменен несколь­кими невырожденными источниками напряжения, которые при необ­ходимости могут быть преобразованы в источники тока с помощью рас­смотренных ранее преобразований.

Вырожденный источник тока, включенный между узлами (k) и (/) произвольной электрической цепи, может быть заменен несколькими источниками тока, включенными параллельно любым ветвям электри­ческой цепи, образующим путь между узлами (k) и (/). Например, вырожден­ный источник тока У, вклю­ченный между узлами (1) и (5) электрической цеп^ (рис. 2.42, а), может бьт заменен двумя источника ми тока, подключенным! параллельно ветвям с ком плексными сопротивления ми Zj, и Z₂, образующим

т, _п п путь между этими же уз

Рнс. 2.42. Перенос идеализированного источни- ■> , „ _т. *

_{ка тока} лами (рис. 2.42, б). Hew

ник тока переносится без изменения тока источника j и его ориента­ции относительно узлов (1) и (3). Эквивалентность цепей следует из того, что процессы в них описываются одной и той же системой уравне­ний электрического равновесия, составленной на основании законов Кирхгофа:

h U+j — Q', ^4,'—£>12 “О,

^2 + Aj—/5 ~ 0; Z₂ /5 “f>23 “0- 0;

В общем случае в результате переноса источника тока вырожденный источник заменяется несколькими невырожденными источниками, ко­торые при необходимости могут быть преобразованы в источники на­пряжения с помощью выражений (2.148). Ветвь, ранее содержавшая вырожденный источник тока, поем переноса источника исчезает.