§ 6.2. Классическии метод анализа

ПЕРЕХОДНЫХ ПРОЦЕССОВ

Свободные и принужденные составляющие токов и

напряжений

Классический метод анализа переходных процессов в линейных инвариантных во времени цепях с сосредоточенными параметрами ос­нован на классическом методе решения обыкновенных дифференциаль­ных уравнений. Как известно, общее решение линейного неоднород­ного дифференциального уравнения с постоянными коэффициентами [см. (1.61)1

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

которое получается из (1.61) при /(0 = 0.

Общее решение однородного дифференциального уравнения (6.5) характеризует так называемые свободные процессы в це­пи, т. е. процессы в цепи после коммутации в отсутствие внешних ис­точников энергии (напомним, что функция f (t) обращается в нуль при выключении всех независимых источников тока и напряжения).

Таким образом, характер свободных процессов ие зависит от вида внешне­го воздействия на цепь, а определяется только параметрами пассивных элемен­тов и линейно управляемых источников, а также топологией цепи после комму­тации.

Свободные процессы в цепи протекают за счет разности энергий, соответствующих установившимся режимам работы цепей до и после коммутации. В связи с тем что эта разность имеет конечное значение, свободные процессы в цепях с потерями с течением времени затухают (в идеализированных цепях без потерь свободные процессы имеют незатухающий характер).

Частное решение уравнения (1.61) определяет принужден­ный режим работы цепи, т.е. режим, задаваемый действующими _в цепи независимыми источниками энергии.

Если внешнее воздействие иа цепь после коммутации изменяется по перио­дическому закону (сохраняет неизменное значение), то частное решение урав­нения (1.61) характеризует установившийся режим цепи после коммутации.

Итак, при использовании классического метода анализа переход­ных процессов искомая реакция цепи у (ток или напряжение какой- либо ветви после коммутации) представляется в виде суммы свободной у_св и принужденной у_пр составляющих:

У — У СП "Ь Упр-

Свободная составляющая реакции цепи с течением времени затуха­ет lim t/_cu = 0, поэтому принужденная составляющая реакции пред-

t-*- 00

ставляет собой установившееся значение искомого тока или напряже­ния после коммутации г/_пр = lim у.

(—>■00

Для определения принужденной составляющей реакции цепи мож­но воспользоваться рассмотренными ранее методами анализа линейных цепей в установившемся режиме. Если после коммутации токи всех независимых источников тока и напряжения всех независимых источ­ников напряжения не изменяются, то с течением времени в цепи после коммутации установится режим постоянного тока. Очевидно, что при­нужденная составляющая реакции цепи в этом случае будет являться постоянным током или напряжением.

Если после коммутации цепь находится под гармоническим воз­действием определенной частоты, то принужденная составляющая ре­акции цепи также будет гармонической функцией времени и для оп­ределения г/_Пр можно воспользоваться методом комплексных ампли­туд.

Если цепь после коммутации находится под воздействием несколь­ких источников гармонических колебаний различной частоты, то, ис­пользуя принцип наложения, мгновенное значение г/_пр можно найти как сумму мгновенных значений частичных токов или напряжений, вызванных в установившемся лосле коммутации режиме каждым из источников в отдельности. Применяя принцип наложения, можно найти принужденную составляющую реакции цепи и тогда, когда внешнее воздействие на цепь х (0 описывается периодической функци­ей более сложного вида, удовлетворяющей условиям Дирих- л е, т. е. имеющей на конечном интервале конечное число максимумов и минимумов и конечное число разрывов первого рода. В этом случае Функция х (() может быть разложена в ряд Фурье (представлена в виде суммы гармонических колебаний кратных частот), а мгновенное зна­чение у„р может быть найдено как сумма мгновенных значений частич­ных токов или напряжений, вызванных в установившемся после ком­мутации режиме каждой из гармонических составляющих внешнего воздействия в отдельности.

Для определения свободной составляющей у_св реакции цепи необ­ходимо найти v корней р, характеристического уравнения

й\р^х + a_v — 1 p^v ~¹ +... -[-a₁ р + a₀ =0, (6.6)

соответствующего однородному уравнению (6.5). Когда все корни урав­нения (6.6) простые (различные), свободная составляющая реакции имеет вид

Усв =^Ai e^Plt + A_z еР>*+ ... +/l_ve^Pvi=2 Л_ге^р*', (6.7)

г-1

т. е. каждому простому корню р_г соответствует слагаемое свободной составляющей вида

4$=Л,еЧ

где A_t—постоянная интегрирования.

Если какой-либо корень p_h характеристического уравнения (6.6)' имеет кратность п, то этому корню соответствует слагаемое свободной составляющей вида

yⁱ_c^k»⁾=(A_l+A₂t + A₃t² + ... +Л_п*»->) eV^eV 2 A,ti~K (6.8)

/=.-1

Характеристическое уравнение (6.6) может иметь вещественные или комплексные корни, причем все корни p_t характеристического урав­нения линейной цепи, составленной из идеализированных пассишшх элементов и независимых источников энергии, расположены в левой полуплоскости комплексного переменного р (включая и мнимую ось): Re Ipi\ ^ 0, так как только в этом случае свободные процессы в цепи имеют затухающий (точнее, ненарастающий) характер.

Общая схема применения классического

метода анализа переходных процессов

Наметим основные этапы классического метода анализа переход­ных процессов в линейных инвариантных во времени цепях с сосре­доточенными параметрами.

1. Анализ цепи до коммутации.В результате этого анализа определяют токи индуктивностей и напряжения емкостей в момент времени, непосредственно предшествующий коммутации (^= = 0_).

2. Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения емкостей в момент времени (t — 0₊). Независимые начальные условия находят с помощью законов коммутации или принципа непрерывности потокосцепления и электри­ческого заряда цепи.

3. Составление дифференциального урав­нения цепи после коммутации (при 0). Дифферен­циальное уравнение цепи получают из системы уравнений электричес­кого равновесия цепи, составленной любым методом, путем исключе­ния всех неизвестных величин, кроме одной, представляющей собой _ток или напряженне какой-либо ветви.

4. Анализ установившегося процесса в це­пи после коммутации (при t->- ос). В результате анализа установившегося процесса в цепи после коммутации находят принуж­денную составляющую реакции цепи (частное решение дифференциаль­ного уравнения цепи).

5. Определение свободной составляющей реакции цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определяют общий вид свободной составляющей реакции цепи (общее решение однородного дифферен­циального уравнения, соответствующего дифференциальному урав­нению цепи после коммутации).

6. Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального урав­нения цепи) находят путем суммирования свободной и принужденных составляющих реакции цепи.

7. Определение постоянных интегрирова­ния. Постоянные интегрирования находят по зависимым начальным условиям (значениям искомых токов или напряжений и их v — 1 пер­вых производных в начальный момент времени после коммутации). Для определения зависимых начальных условий используют незави­симые начальные условия и уравнения электрического равновесия цепи после коммутации.

8. Определение реакции цепи, соответству­ющей заданным начальным условиям. Подстав­ляя постоянные интегрирования в общее решение дифференциально­го уравнения цепи после коммутации, находят частное решение диф­ференциального уравнения, соответствующее заданным начальным условиям, т. е. искомый ток или напряжение одной из ветвей при t> 0.

Переходные процессы в последовательной

^С-цепи при скачкообразном изменении э. д. с.

Рассмотрим переходные процессы в последователоной ^С-цепи (рис. 6.4, а) при скачкообразном изменении э. д. с. идеализированно­го источника постоянного напряжения

Г£_1При*<°;

( Е₂ при t ^ 0.

Такое изменение э. д. с. источника напряжения происходит напри- ^МеР, когда в цепи, схема которой приведена на рис. 6.4, б, ключ 5 в Момент времени t = 0 перебрасывают из положения 1 в положение 2.

Очевидно, что в момент времени, непосредственно предшествовавший коммутации, напряжение на емкости равнялось напряжению на за­жимах источника энергии при t < О (предполагается, что до коммута­ции цепь находилась в установившемся режиме). Используя второй закон коммутации, находим единственное независимое начальное ус­ловие

«с (0+) = «с (0-) = Ei. (6.9)

Дифференциальное уравнение рассматриваемой цепи можно сос­тавить относительно любой из неизвестных величин (напряжения на сопротивлении м_д, напряжения на емкости м_с, тока сопротивления

R 1 " UC~U СПр + Uccfi 12 3 4- ■ l_j L_ tVc =*=.<? J— I (EZ-E,)/K ь/хс ,0i23 4t/Zc 6) Ur.
	ft
	V:	UccS -L. Г
G	i z	3 Ц-
ic	o' 1 2	3 4

te = LccS У e(t)
£2	E,
	t
Uc	/Ucnp ^спр*иссИ E4 Z 3 if-
0

^lc~ ^ъссв

о i г з bt/%o

д)

Рис. 6.4. К исследованию переходных процессов при скачкообразном изменении э. д. с. в последовательной RC-цепи: а, б — схемы цепи; в — £» = 0; г — Е_г = 0; д — Ез>Е]>0

i_R, тока емкости i_c), однако, учитывая, что для данной цепи известно начальное значение напряжения на емкости, целесообразно составить уравнение относительно этого напряжения.

^duC.

dt ’ t; Mr = Rijj

Исключая из основной системы уравнений электрического равно­весия цепи при t ^ 0

Mr -j- Uc — Е*\ ic — С ic =■ ^lR

_все неизвестные величины, кроме и_с, получаем

UU/1

RC ———j- Uc = £₂.

at

(6.10)

Напряжение на емкости при t ^ 0 представим в виде суммы при­нужденной и свободной составляющих

— Не пр + Ч'СС'В’

Очевидно, что с течением времени после коммутации в цепи должен установиться режим постоянного тока, причем установившееся зна­чение тока емкости будет равно нулю (сопротивление емкости посто­янному току бесконечно велико), а установившееся значение напря­жения на емкости — напряжению источника энергии после коммута­ции. Таким образом, принужденная составляющая напряжения на емкости

(6.11)

Характеристическое уравнение цепи

RCp + 1 = 0

имеет единственный корень

_Pl = -1/ (RC) = -1/т_с,

где т_с — RC — постоянная времени последовательной RC-цепи, по­этому свободная составляющая напряжения на емкости и_сов содер­жит один экспоненциальный член

(6.12)

иссв = А е^' = А_г е ^t/Tc,

Используя выражения (6.10), (6.11) и (6.12), находим напряжение на емкости после коммутации при произвольных начальных условиях

(6.13)

u_c = E_i + A_l e-^J/Tc.

Для определения постоянной интегрирования А_г воспользуемся независимым начальным условием (6.9). Полагая в (6.13) t — 0, и_с = ~ ^ис (0+) = Е_ъ получаем Е_х — £₂ -f- A_lt откуда А_х — E_t— Е₂.

Таким образом, при заданных начальных условиях напряжение на емкости после коммутации (t ^ 0) определяется выражением

(6.14)

u_c = E₂~(E₂~E_l)e-^tlXc,

Зависимость напряжения на емкости от времени при различных соотношениях между и Е._г показана на рис. 6.4, в— д. Здесь же по­казана зависимость от времени тока емкости i_c, которая при t ^ 0 определяется путем дифференцирования выражения (6.14) по времени и умножения результата на С:

(6.15)

Как видно из рисунка, в начальный момент после коммутации на­пряжение на емкости сохраняет то же значение, что и до коммутации, а затем плавно изменяется, стремясь в пределе к новому установив­шемуся значению. Ток емкости в начальный момент скачком изменя­ется от нуля до начального значения:

*'с (0+) = (Е, — EJ/R, (6.16)

а затем плавно уменьшается, стремясь в пределе к нулю. В связи с тем что установившееся значение тока емкости до и после коммутации рав­но нулю, ток рассматриваемой цепи содержит только свободную сос­тавляющую.

Анализ выражения (6.16) показывает, что значение тока емкости t'c (0+) численно равно постоянному току, который протекал бы в це­пи после коммутации, если бы емкость С была заменена идеальным источником напряжения э. д. с. Е_л. Следовательно, в начальный момент времени после коммутации емкость ведет себя подобно источнику на­пряжения, э. д. с. которого равна начальному значению напряжения на емкости. Если начальное значение напряжения на емкости равно нулю, то в начальный момент после коммутации ветвь с емкостью можно счи­тать короткозамкнутой, т. е. сопротивление емкости равно нулю.

Далее (см. пример 6.4) будет показано, что в начальный момент времени после коммутации индуктивность ведет себя подобно источ­нику тока, ток которого равен начальному значению тока через ин­дуктивность. При i_L (0_) = 0 ветвь с индуктивностью в начальный момент времени можно считать разомкнутой, т. е. сопротивление ин­дуктивности при t - 0₊ имеет бесконечно большое значение.

Как видно из выражений (6.12) и (6.15), скорость затухания сво­бодных составляющих тока и напряжения емкости не зависит от Аа- чения э. д. с. идеализированного источника напряжения до и после коммутации, а определяется только постоянной времени цепи х_с, ко­торая численно равна промежутку времени, в течение которого сво­бодные составляющие тока и напряжения уменьшаются в е « 2,718 раз. Можно показать, что при любом t ^ 0

	“с СВ	1 *св
■1 с =	d“CcJdt	1 dtCBfdt

Таким образом, постоянная времени рассматриваемой цепи чис­ленно равна длине подкасательной к кривой ы_Ссв или i_CCB при любом значении t ^ 0, т. е. длине отрезка временной оси, заключенного меж­ду какой-либо точкой t = ^>0и точкой пересечения временной оси касательной, проведенной к кривой и_Ссв или 1_Ссв в точке ы_Ссв (f_x) или t’t’cn (ti) Для определения постоянной времени цепи касательную к кривым i_rca или «_гсн наиболее удобно проводить при t\ = 0. В этом случае она пересекает ось времени в точке t — (рис. 6.4, в—д).

Чем больше постоянная времени цепи, тем медленнее затухают свобод­ные составляющие токов и напряжений и, следовательно, токи и напряжения цепи медленнее приближаются к установившимся значениям.

Теоретически процесс установления нового режима длится беско­нечно долго, однако, учитывая, что к моменту времени, равному 4т_с после коммутации, свободные составляющие уменьшаются да уровня менее 0,02 от начального значения, переходные процессы в цепи можно считать практически закончившимися через промежуток времени (4ч-5)т_с после коммутации.

Подключение к последовательной ^L-цепи источника гармонического напряжения

Рассмотрим переходные процессы в последовательной 7?/.-цепи, содержащей идеализированный источник, э. д. с. которого е (t) изме­няется во времени по закону

(6.17)

0 при ^ С 0;

Е_т cos {a>t + i|i) при ^ 0.

Временная диаграмма е (t) при г)э;>0 приведена на рис. 6.5, а. В этом случае ток индуктивности в момент времени, непосредст­венно предшествующий коммутации, i_L (0_) = 0.

e(t)

Е-т

v^z

г

I

Рис. 6.5. К исследованию переходных процессов при включе­нии источника гармонического напряжении в последовательную

RL-цепь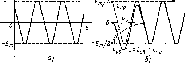

Дифференциальное уравнение цепи, составленное относительно то­ка i = i_L> при 0 имее^ вид

(6.18)

¹ ~~Ь + ^{Ri = Е}™ ^C0S + *) •

dt

Принужденная составляющая тока может быть найдена с помощью метода комплексных амплитуд

t_np " COS (<й/ -f- t{J — ф),

где г -- У R² •+ (сoL)², ср = arctg (соL/R) —»модуль и аргумент комп­лексного входного сопротивления рассматриваемой цепи. Характеристическое уравнение цепи

имеет единственный корень р_х = —R/L, поэтому свободная состав­ляющая тока содержит один экспоненциальный член

‘■ев ^Л1^е >

где x_L — L/R — постоянная времени последовательной RL-цепи.

Суммируя свободную и принужденную составляющие, находим общее решение дифференциального уравнения цепи (6.18) после ком­мутации:

i = -^2- cos (u)t + гр—ф)+А^{е /Xl} . (6.19)

Для определения постоянной интегрирования А_г воспользуемся первым законом коммутации, в соответствии с которым начальное значение тока рассматриваемой цепи должно равняться нулю:

f(0₊)=M0+)~¹_t(0_)=0. ‘ (6.20)

£

Подставляя (6.20) в выражение (6.19), получаем ■— cos (if — ф) + + = 0, откуда

А_х = — cos (яр— ср). (6.21)

г

С учетом (6.21) выражение для тока рассматриваемой цепи после коммутации принимает вид

i =-^2Ь. cos (u>t + яр — ср) [cos (яр —-ф)] е *^,XL .

z г

Характер переходных процессов зависит от соотношения между начальной фазой яр э. д. с. идеализированного источника напряжения и аргументом ф входного сопротивления цепи. Если яр выбирают таким образом, что начальные значения принужденной t_up (0+) и свободной (_си (0составляющих равны нулю (яр = ф ± л/2), то свободная сос­тавляющая тока тождественно равна нулю. Переходные процессы в цени в этом случае отсутствуют, т. е. установившийся режим насту­пает сразу же после коммутации. При яр = ф или яр — ф ± л началь­ные значения свободной и принужденной составляющих максималь­ны, и отличие в форме кривых i — i (t) и t'_np = t„_p (t) выражено наи­более резко (рис. 6.5, б).

Как и для последовательной RC-цепи, скорость затухания свобод­ной составляющей тока рассматриваемой цепи не зависит от характе­ра внешнего воздействия, а определяется только постоянной времени %j_. За промежуток времени t - t_l свободная составляющая тока уменьшается в е раз и к моменту времени t -- (4 ■— 5)т_ь после комму­тации переходные процессы в цепи можно считать практически закон­чившимися.

Подключение к последовательной RLC-цепи источника постоянного напряжения

Последовательная RLC-щтъ содержит два независимо включен­ных реактивных элемента, поэтому процессы в ней описываются диф­ференциальным уравнением второго порядка, а для определения по­стоянных интегрирования необходимо задать два независимых началь­ных условия. Если э. д. с. идеального источника напряжения изменя­ется во времени по закону

f 0 при ^ < 0;

1 Е — const при t ^0, то независимые начальные условия цепи имеют нулевые значения

и_с (0₊) = и_с (0_) = 0; i_L (0₊) = i_L (0_) - 0. (6.22)

Составим уравнение электрического равновесия цепи по методу токов ветвей

<

^L4T ^{+ Ri + ис (}° ^{+) +} -£-j^idt = ^E- (6.23)

О

Дифференцируя правую и левую части (6.23), получаем диффе­ренциальное уравнение рассматриваемой цепи после коммутации

^L-ir^+R-%-+±ⁱ⁼⁰- ⁽⁶-²⁴⁾

Для определения единственного решения этого уравнения, соот­ветствующего заданному режиму работы цепи до коммутации, необ­ходимо определить начальные значения тока цепи и его первой произ­водной по времени. Начальное значение тока цепи совпадает с началь­ным значением тока индуктивности

i (0₊) -- I,. (0₊) = 0, (6.25)

а начальное значение первой производной тока цепи по времени мо­жет быть найдено с использованием независимых начальных условий (6.22) и уравнения электрического равновесия цепи (6.23) при t= 0„ =0;

di

= -f . (6.26)

dt

<---о₊ L

В связи с тем что установившееся значение тока этой цепи после коммутации равно нулю,ток при t > 0 содержит только свободную со­ставляющую: i -= t'cB •

Характеристическое уравнение последовательной RLC-цепи

Lp² + Rp + 1/С = О (6.27)

-®0,

<еет два корня

(6.28)

хе 6 = R/(2L) — коэффициент затухания; ц>₀ = 1 /УLC— резонанс- ая частота цепи. В зависимости от соотношения между величинами >₀ и 6, или, что то же самое, в зависимости от добротности цепи,

л 1/ ^L _^_^ыо^L --

R R V С R 28 ’

орни характеристического уравнения (6.27) могут быть вещественны- ш различными, комплексно-сопряженными или вещественными динаковыми (кратными). Рассмотрим каждый из этих случаев.

Вещественные различные корни. При малой юбротности последовательной RLC-цепн (Q < 1/2, т.е. R >■ 2р и i > ю₀) характеристическое уравнение (6.27) имеет два различных ве- цественных отрицательных корня, а выражение для тока цепи после <оммутации (t > 0) содержит два экспоненциальных члена:

i=*i_CT!=A_le^p‘^t + A₂e^p’^t. (6.29)

Дифференцируя правую и левую части выражения (6.29) di/dt — -= р₁Л₁е^Р1* + р₂А_ге^р‘* и используя зависимые начальные условия (6.25), (6.26), составляем уравнения для определения постоянных ин­тегрирования А_г и Л₂: А₁-\_ГА₂ = 0; _PlA_x + р₂А₂ = Е/L, откуда

_Л . ^{Е Е} ;

L(_Pl-p₂) 2L У6'-'—о)3 ’

-Е -Е

А, =

L (Pi— Рг) 21 У6²—tog •

С учетом (6.30) выражение для тока цепи после коммутации прини­мает вид

Е

(ePi t е^р2*).

21 У б²

Расположение корней р_ъ р., характеристического уравнения в плоскости комплексного переменного р и зависимость нормированного тока рассматриваемой цепи от времени

J =. ²¹ ..i = ePit——JiD_П{2)

Е

приведены на рис. 6.6, а. Переходной процесс в цепи носит аперио­дический (неколебательный) характер, причем вследствие того, что \p-i!, вторая составляющая нормированного тока цепи /⁽²⁾

затухает быстрее, чем первая t^<3).

Комплексно-сопряженные к и _н „ ... добротности последовательной tfLC-цепи (Q> 1/2, т. е.‘ R < 2р и б С ю₀) характеристическое уравнение (6.27) имеет два комплексно­сопряженных корня

/>1,2 = —б ± /ш_св,

где ю_св = — S² — частота свободных колебаний в цепи (смысл

этого понятия будет ясен из последующего изложения). Ток цепи пос­ле коммутации, как и в предыдущем случае, определяется выражением

Im PrPz Re а) -E(a>cet) - Рис. 6.6. Расположение корней характеристического уравнения в плоскости комплексного переменного и зависимость свободной составляющей тока после­довательной RLC-цепи от времени для: я — (Оо; б ~ б<соо; в — 6*0; г — б~сов n L=ie'‘ s 1лш г) -1 1т рг, р<	Im /1 / I 1	.. Il77 b>0 ac3 . f P’	0)q
-9	Re -°>o\ i-fr \ i	0 Re i-a>0	0 Re
		-<°C6 \.
i	i	-<*0 p yz	■<o0

i i

in

29. , которое после нахождения постоянных интегрирования А_г — — £/(/2<o_CBL), А₂ — — £7(/2<d_cbL) может быть с учетом соотношения

е^/шсв‘_е^_/“^св<

= sin (й„„ t

2/ ^св

преобразовано к виду Е

i = е-“ sin (o_OB t = /_m (t) cos (ш_св t—я/2),

w_CB ^L

где I_m (_t) = £e-«/(«,_CBL).

Таким образом, при включении в последовательную /^LC-цепь с высокой добротностью идеального источника постоянного напряжения переходные процессы в ней имеют колебательный харак- ^{т е} P - Ток цепи представляет собой затухающую гармоническую функ­цию, амплитуда которой экспоненциально уменьшается во времени. Колебательный характер переходного процесса в цепи связан с перио­

дическим обменом энергией между емкостью и индуктивностью, а за­тухание колебаний объясняется потерями энергии в сопротивлении.

Расположение корней р_и /?₂ характеристического уравнения в плоскости комплексного переменного р и зависимость тока цепи от вре­мени показаны на рис. 6.6, б. Корни характеристического уравнения расположены симметрично относительно действительной оси в левой полуплоскости на полуокружности с радиусом, численно равным ре­зонансной частоте последовательного колебательного контура ю_в. Чем меньше коэффициент затухания б, тем ближе к мнимой оси распо­ложены корни уравнения, меньше различие между со_св и ю₀ и медлен­нее затухание свободных процессов. В пределе, при 6 = 0, корни ха­рактеристического уравнения располагаются на мнимой оси, частота свободных колебаний совпадает с резонансной частотой цепи, а колеба­тельные процессы в цепи носят незатухающий характер (рис. 6.6, в). Таким образом, резонансная частота RLC-цепи численно равна частоте свободных колебаний в цепи, когда коэффициент затуха­ния б равен нулю.

Пунктирными линиями на рис. 6.6, б показаны кривые ± l_m (t), которые характеризуют закон изменения амплитуды тока во времени. Эти кривые называются огибающими. Величина, численно рав­ная длине подкасательной к огибающей тока, т = 1/6 = 2L/R называ­ется постоянной времени последовательной RLC-цепи. Очевидно, что за промежуток времени t — т ордината огибающей тока уменьшается в е раз. Скорость затухания свободных процессов в рас­сматриваемой непи может быть охарактеризована также логариф­мическим декрементом колебаний 0, который ра­вен натуральному логарифму отношения двух максимальных значений тока, взятых через период свободных колебаний Т_св = 2я/ю_св = = 2 л 1у <йо—■ б².

Находя натуральный логарифм отношения ординат огибающих то­ка для t_x > 0 и + Го, можно прийти к выводу, что логарифмичес­кий декремент колебаний ие зависит от выбора t_lt а определяется толь­ко добротностью цепи Q:

0 = 1п ЬвМ = 6Г_СВ—²-^я6 — = ^я- . (6.31)

ImUi + Тсв) Vb>l — 5² VC}²— 0,25

Анализ выражения (6.31) показывает, что логарифмически# декре­мент колебаний равен нулю при 6 = 0 (Q = оо) и обращается в бес­конечность при 6 = м₀ (Q = 1/2).

Кратные корни. При Q = 1/2, т. е. при R = 2р и б = со», характеристическое уравнение последовательной RLC-цепи имеет два одинаковых вещественных корня Pi = р₂ — — б, расположенных на отрицательной вещественной полуоси в плоскости комплексного пере­менного р (рис. 6.6, г). Как следует из выражения (6.8), общее решение дифференциального уравнения (6.24) при t > 0 в этом случае имеет вид

Определяя с помощью зависимых начальных условий (6.25) и (6.26) значения постоянных интегрирования А, = 0, Л_г = Е/L и подставляя их в выражение (6.32}, получаем окончательно

i - Ete~⁶ⁱIL.

Как и для вещественных различных корней, переходный процесс в цепи при одинаковых вещественных корнях имеет апериодичес­кий характер (рис. 6.6, г), поэтому условие Q = 1/2 является предельным условием существования в цепи апериодических свобод­ных процессов. Режим работы цепи на границе между колебательным и апериодическим характерами переходных процессов называется критическим.

Итак, характер переходных процессов в последовательной Л/,С-цепп пол­ностью определяется расположением корней характеристического уравнения в плоскости комплексного переменного.

Зарисимость характера переходных процессов от расположения корней характеристического уравнения в плоскости комплексного пере­менного присуща не только последовательной 7?1С-цепи, она является общим свойством линейных электрических цепей любого порядка слож­ности.

Подключение к последовательной RLC-цепи источника

гармонического напряжения

Рассмотрим важный для практики случай включения источника гар­монического напряжения в последовательную RLC-цепь с высокой доб­ротностью (Q > 1/2). Свободные процессы в такой цепи, как было ус­тановлено ранее, имеют колебательный характер. Пусть идеализиро­ванный источник напряжения включен в цепь в момент времени t ^=0, причем примем, что мгновенное значение э.д.с. этого источника при t = 0 равно нулю (г)э = — я12). Уравнение электрического равновесия такой цепи после коммутации, составленное по методу токов ветвей, имеет вид

t

^ + Ы_С (°+) + -^Г j' idt = Е_т sin at, (6.33)

о

а дифференциальное уравнение цепи

L + R ~ +-^ i = а>Е_т cos at. (6.34)

Для решения уравнения (6.34) необходимо определить начальные значения тока цепи i (0+) и его первой производной по времени ^ |_fs=0+ Используя независимые начальные условия

и_с (0₊) = и_с (0_) = 0; i_L (0₊) = i_L (0_) = 0

и уравнение электрического равновесия (6.33), получаем i(0₊) = /_L(0₊)=0; ^di

= 0.

(6.35)

(6.36)

(6.37)

(6.38)

Здесь I_mn p = EJV R² + — 1/wC)² — амплитуда принужден-

dt

t=o_

Далее, суммируя составляющие тока

*'пр =/т пр cos (cot -НФ—ф) =/_т пр sin (<tf—ф); i_CB е^—(^в-,’“св)¹ -\-А₂ е-(^в+/<лсв)^<,

находим общее решение уравнения (6.34) при t > 0:

i = Л»пр sin (at—ф) + [Л! е^,“св^< + Л₂ е^_/"ев *] _е'

б<

coL — 1/со С

X

ной составляющей тока; ф = arctg

— аргумент комп­

лексного входного сопротивления рассматриваемой цепи.

Для определения постоянных интегрирования А_х, А₂ продифферен­цируем правую и левую части (6.38)

-(6 —/а>_Св) I

di

— =®/m пр COS (ttrf—ф)— А_х (б!—/ш_св) е

-Л₂ (б+у_Шсв)е'-(^б+/“св)‘

“ев/ ^ (6.39)

и подставим в выражения (6.38) и (6.39) зависимые начальные условия (6.35). Решая полученную таким образом систему уравнений относи­тельно A j и А ₂, находим

_л _ (6-Н<в_св) sin ф—со cos ф _т ^Л1 — *1

¹ тпр»

2/со_с

„ О)

cos <р—(6— /со_св) sin ф J

'тпр-

2/Исв

(6.40)

С учетом соотношений (6.40) выражение (6.37) для свободной состав­ляющей тока может быть преобразовано к виду

6 sin ф со cos

+ е

. sin ф +

й>св <**св

_е—м jsin ф cos ю_св ^ + sin ю_ов п /_тпр е

X

' гг пр

2

6 sin ф

О) COS Ф

(6.41)

+

0>СВ

0)_Св

Предположим, что частота <о внешнего воздействия близка к часто­те <й_св свободных колебаний, а добротность Q настолько велика, что а)_св практически совпадает с резонансной частотой цепи <о₀. С учетом этих допущений, которые незначительно уменьшают общность получа­емых результатов, выражение (6.41) существенно упрощается:

•'св = (sin ф cos a>₀i— cos ф sin a>₀t) I_mnp e^-M =

= — 1 mnp e-^w sin (<V — ф).

Таким образом, в последовательной RLC-цепи, удовлетворяющей принятым допущениям, свободная составляющая тока является зату­хающей гармонической функцией времени. В начальный момент време­ни амплитуда свободной составляющей тока равна амплитуде принуж­денной составляющей, а затем уменьшается по экспоненциальному за­кону. Через промежуток времени, равный (4ч-5) т после коммутации, амплитуда свободной составляющей становится пренебрежительно малой по сравнению с амплитудой принужденной составляющей, и переходной процесс в цепи можно считать практически закончившим­ся.

Рис. 6.7. Зависимость тока последовательной RLC-цепи от времени при включении источника гармонического напряжения:

а — ы=»соо. 6^0; б — м^Ио, 6=-0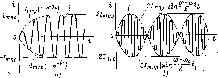

Ток цепи после коммутации равен сумме свободной и принужден­ной составляющих:

i = /_тпр sin (at — ср) — /_тпр е-⁶' sin (м₀/ — ср). (6.42)

Если частота внешнего воздействия м в точности совпадает с резо­нансной частотой цепи w₀, то входное сопротивление цепи имеет чисто резистивный характер (ср = 0) и выражение (6.42) принимает вид (рис. 6.7, а)

i = /muр (1 — е-“) sin <a₀t. (6.43)

Как видно из рисунка, амплитуда тока цепи при ш = ю₀ плавно увеличивается во времени, стремясь в пределе к установившемуся зна­чению /_тпр. Ни при каких значениях t амплитуда тока после комму­тации не превышает этого значения.

При включении в последовательную RLC-цепь источника гармони­ческого напряжения, частота которого близка к резонансной, но не равна ей, в цепи наблюдаются биения, заключающиеся в периоди­ческом увеличении амплитуды тока или напряжения до значения, значительно превышающего амплитуду принужденной составляющей (рис. 6.7, б). Если пренебречь затуханием свободной составляющей тока (б = 0), то из выражения (6.42) получаем

i = ^2/m пр Sin ^ COS p£±^<L. _t — cpj =

= /_m(/) cos(-^-p- /-фу (6.44)

Как видно из этого выражения, ток цепи имеет частоту, близкую к резонансной, а амплитуда тока I_m (t) медленно изменяется во време­ни:

/_т (0 = 2/_т „р | sin t , (6.45)

причем максимальное значение тока в переходном режиме в два раза превышает амплитуду принужденной составляющей..

Возникновение биений при включении источника гармонического напряжения в последовательную RLC-цепь объясняется тем, что вследствие несовпадения частот внешнего воздействия и свободных ко­лебаний фазовые соотношения между свободной и принужденной сос­тавляющими тока непрерывно изменяются, а разность мгновенных фаз этих колебаний (ю — u>₀)t линейно нарастает во времени. В те моменты времени, когда разность мгновенных фаз будет равна 2kn, где k= 0, 1, 2, .... сумма мгновенных значений /_св и i_nv будет максимальна, а в те моменты времени, когда разность фаз будет равна (26+1)л,—мини­мальна. Частотой биений называют частоту повторения максимумов огибающей тока (6.45). Угловая частота биений, таким образом, равна абсолютному значению разности угловых частот свободной и принуж­денной составляющей

®б = I® — “ol-

В реальных колебательных контурах коэффициент затухания 6 имеет малое, но конечное значение. Свободная составляющая тока в таких контурах экспоненциально уменьшается во времени, а биения носят затухающий характер.