§ 5.3. Аппроксимация характеристик

НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЭЛЕМЕНТОВ

Задача аппроксимации

Вольт-амперные характеристики реальных элементов электричес­ких цепей обычно имеют сложный вид, их представляют в виде графи­ков или таблиц экспериментальных данных. В ряде случаев непосред­ственное применение ВАХ, задаваемых в такой форме, оказывается неудобным и их стремятся представить в виде достаточно простых аналитических соотношений, хотя бы качественно отражающих харак­тер рассматриваемых зависимостей. Замена сложных функций прибли­женными аналитическими выражениями называется аппрокси­мацией (от лат. approximare — приближаться).

Аналитические выражения, аппроксимирующие ВАХ нелинейных резистивных элементов, с одной стороны (для повышения точности и достоверности анализа) должны как можно более точно описывать ход реальных характеристик, а с другой — повышение точности аппрок­симации приводит, как правило, к усложнению аппроксимирующих выражений, что затрудняет как определение значений входящих в эти

выражения коэффициентов, так и применение этих выражений для анализа цепи. В связи с тем что характеристики однотипных нелиней­ных резистивных элементов от экземпляра к экземпляру отличаются за счет производственного разброса параметров и погрешности измере­ний, нецелесообразно стремиться получить аппроксимирующие выра­жения, точность которых превышает точность определения характе­ристик отдельных элементов. Таким образом, при решении задачи ап­проксимации так же, как и при решении любой задачи, связанной с вы­бором расчетной модели, необходимо идти на компромисс между точ­ностью и сложностью модели.

Успешное решение задачи аппроксимации в значительной степени зависит от ширины аппроксимируемой области ВАХ, т. е. от диапазо­на, в котором могут изменяться токи и напряжения исследуемого эле­мента. Как правило, чем уже область аппроксимации, тем более про­стой функцией может быть описана соответствующая ВАХ.

Задача аппроксимации ВАХ включает в себя две самостоятельные задачи: выбор аппроксимирующей функции и определение значений, входящих в эту функцию постоянных коэффициентов.

Выбор аппроксимирующей функции

Функцию, аппроксимирующую ВАХ какого-либо нелинейного ре­зистивного элемента, выбирают либо исходя из физических представ­лений о работе данного элемента, либо чисто формально, основываясь на внешнем сходстве ВАХ с графическим изображением той или иной функции. Для аппроксимации ВАХ используют как элементарные, так и различные трансцендентные функции, а также степенные, экспонен­циальные и тригонометрические полиномы и кусочно-линейные функции.

Так как внешнее сходство ВАХ с графическим изображением функ­ции, выбранной в качестве аппроксимирующей, может оказаться об­манчивым, перед тем, как перейти к определению значений коэффици­ентов соответствующей функции, желательно проверить возможность ее применения, используя метод выравнивания. Сущность этого метода заключается в том, что для проверки гипотезы о виде функциональной зависимости у -- у (х), заданной множеством значе­ний Xj, yj, переменные х и у заменяют некоторыми новыми переменны­ми X - /, (х, y)\Y- - /₂ (х, у), которые выбирают таким образом, что­бы при сделанных допущениях о виде функции у = у (х) переменные У и X были связаны между собой линейной зависимостью

(5.4)

Таким образом, если проверяемая гипотеза о виде функции у - у (х) справедлива, то точки X, - f_Y (х_}, у_}), Yj - /₂ (x_Jt yj) должны распо­лагаться на одной прямой.

(5.5)

Если предполагается, что заданная зависимость описывается сте­пенной функцией

то, логарифмируя левую и правую части выражения (5.5) lg у =- lg а + b lg х, нетрудно прийти к выводу о том, что зависимость между вспомогательными переменными У -= \g у я X = \g х должна иметь линейный характер:

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

линейный вид должна иметь зависимость Y Ау от X - л:, где Ау - у_} — Уз— 1 — разность значений функции у (х), соответствующих двум соседним значениям аргумента Xj и х_}-_х (предполагается, что значения аргумента образуют арифметическую прогрессию с шагом h).

Если заданная зависимость у - у (х) аппроксимируется экспонен­циальным полиномом вида

у - ae^hx t- с, (5.10)

то линейной зависимостью

У - lg а + ф lg е)Х (5.11)

должны быть связаны вспомогательные функции Y = lg (у — с) и X = х. Для определения с выбирают три значения аргумента х_х, ^х2> х₃ — (-*1 + ^хг)/2 и соответствующие им три значения функции у_х, уи у₃, которые затем подставляют в выражение

с (У\У2 — У1)' {У\ + Уг — 2г/₃). (5.12)

Если при проверке гипотезы о виде аппроксимирующей функции методом выравнивания окажется, что зависимость между вспомога­тельными переменными X и Y имеет линейный характер только в оп­ределенном диапазоне изменения X, то, следовательно, данная гипо­теза справедлива только в соответствующем диапазоне изменения аргумента исследуемой функции уj (xj).

• ••••

Пример 5.5. На рис. 5.20, а изображена прямая ветвь ВАХ кремниевого диода. Проверим, можно ли аппроксимировать эту характеристику полиномом второй степени (5.9).

Выбираем шаг изменения аргумента h - 0,2 В и рассчитываем значения вспомогательной переменной Y -- \у — yj — У]-\. соответствующие выбран­ным значениям аргумента (рис. 5.20, б). Как видно из рисунка, зависимость У

ъ, мА у

а) 5)

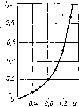
Рис. 5.20. К примеру 5.5

от X практически совпадает с линейной при изменении X - х в пределах от 0 до 1 В, следовательно, в этой области рассматриваемая В АХ может быть ап­проксимирована полиномом второй степени.

• ••••

Пример 5.6. Проверим, можно ли аппроксимировать ВАХ диода (см рис. 5 20, а) с помощью экспоненциального полинома вида (5.10).

Для определения константы с выберем три значения аргумента дг, 0, х._г — 1, х₃~ 0,5 и найдем соответствующие им значе­ния функции ih -- 0, у₂ -- 0,3 и у_я -= 0,095.

Подставляя эти значения в выражение (5.12), получаем с - —0,082. Далее строим зависи­мость вспомогательной функции У lg (у —

— с) от X х (рис. 5.21). Как видно из рисунка, в пределах от X — 0 до X = 1 за­висимость Y (X) практически совпадает с линейной, следовательно, в этой области рас­сматриваемая ВАХ может быть аппрокси­мирована экспоненциальным полиномом рассматриваемого типа.

Из приведенных примеров следует, что задача выбора аппроксимирующей функции не имеет единственного реше­ния. Выбор той или иной функции во

многом зависит от опыта и интуиции исследователя и в значитель ной степени определяется простотой нахождения значений коэффи циентов функции и удобством ее применения для анализа.

Определение коэффициентов аппроксимирующей функции

Рассмотрим кратко основные методы определения коэффициентов аппроксимирующей функции. Наиболее часто для этой цели исгшль- зуют метод выбранных точек, в соответствии с которым зна­

чения коэффициентов аппроксимирующей функции определяют исходя из совпадения значений этой функции со значениями аппроксимируй мой функции в ряде заранее выбранных точек, называемых узла­ми интерполяции (от лат. interpolare — подновлять). Если для аппроксимации ВАХ, задаваемой множеством точек {xj,y_}}_t выбрана функция

У = У (х, а_г, а₂, а_п), (5.13)

имеющая п неизвестных постоянных коэффициентов а_и а₂, ...,а„, то для определения этих коэффициентов выбирают п наиболее характер­ных точек ВАХ, лежащих в пределах рабочей области. Подставляя значения xj и yj в каждой из выбранных точек в выражение (5.13), по­лучают систему из п уравнений у, -= у (ха_х, а.₂, ..., а_п), решая кото­рую, находят значения всех неизвестных коэффициентов. Очевидно, что такой выбор коэффициентов действительно обеспечивает совпаде­ние значений аппроксимируемой и аппроксимирующей функций в уз­лах интерполяции, однако в промежутках между ними погрешность аппроксимации может быть весьма существенной (информация о ходе аппроксимирующей функции в них не учитывается), что является недостатком этого метода.

В отличие от метода выбранных точек метод наименьших квадратов обеспечивает наименьшую сумму квадратов отклоне­ний | значений аппроксимирующей функции у = (х, а_г, а₂, ..., а_п) от значений исходной функции у, (xj) в произвольном числе точек т, не связанном с числом неизвестных коэффициентов п:

т

I = 2 \У ^а" ^а2’ ^ап)—У}]*-

/=1

Приравнивая нулю первые производные £ по каждому из коэффи- * циентов, получаем систему из п уравнений для определения п неиз­вестных числовых значений коэффициентов:

т

= \ ■■■«■> „0;

да_х i-* дщ

основы 1

ТЕОРИИ ЦЕПЕЙ 1

да© 28

-“+²т^(‘~т^Л“—r‘^fal^L)+ 70

*т-т 89

ГН 181

х 212

J 242

От 265

1М-[: 445

й-йма-ь&Ч:;:]- 471

щ;:у:у. ' ПП 521

оа_п да_п

Метод наименьших квадратов требует весьма громоздких вычис­лений и применяется обычно только в тех случаях, когда необходима высокая точность аппроксимации.

Если гипотеза о характере аппроксимирующей функции прове­рялась методом выравнивания, то неизвестные значения коэффициен­тов аппроксимирующей функции могут быть определены по известным

значениям коэффициентов К₀ и линейного уравнения (5.4), связы­вающего между собой значения вспомогательных переменных X и Y. Составляя уравнение прямой линии, вдоль которой располагаются точки Xj, Yj, и сравнивая его с уравнением, описывающим зависи­мость между вспомогательными переменными, которое соответствует проверяемой гипотезе о виде функции у (х) [например, с уравнениями (5.6), (5.8) или (5.11)1, находим значения искомых коэффициентов.

• ••••

Пример 5.7. Определим значения коэффициентов экспоненциального поли­нома i = ae^bu -f с, аппроксимирующего ВАХ кремниевого диода (см. рис. 5.20, а) в диапазоне напряжений от 0 до 1 В.

Возможность аппроксимации ВАХ, приведенной на рис. 5.20, экспоненциаль­ным полиномом указанного типа была показана в примере 5.6. Там же было най­дено числовое значение коэффициента с. Составим уравнение прямой (рис. 5.21), на которой в рассматриваемом диапазоне изменения аргумента располагаются точки Xj, Yj-.

(Y - Y_x)/(Y₂ - У,) - (X - X_t)/(X, - X,).

Здесь Xj, У', и Х₂, У•> —координаты двух любых точек, через которые проходит данная прямая. Выбирая X, = 0,2, К, — —0,95 и Х₂= 1, = —0,42, по­

лучаем уравнение прямой в следующей форме:

Y = 0.66Х — 1,08.

Сравнивая это выражение с выражением (5.11), получаем соотношения для определения неизвестных значений коэффициентов а и Ь:

lg а = —1.08; b lg е = 0,66,

откуда а -- 0,082, Ь = 1,52.

Таким образом, в диапазоне от 0 до 1 В рассматриваемая ВАХ может быть аппроксимирована выражением, мА,

(=0,082 (е¹'⁵²"— 1).

На практике для аппроксимации характеристик нелинейных эле­ментов в основном используют степенные полиномы

У - а₀+ а,х + а₂х² + ... + а_пх^п (5.14)

и кусочно-линейные функции. Аппроксимация с помощью степенно­го полинома универсальна и позволяет повышать точность расчета путем увеличения степени поли­нома.

Любые аппроксимирующие функции могут быть разложены в степенные ряды и приведены к виду (5.14). Поскольку слож­ность определения значений коэффициентов аппроксимирую­щей функции возрастает с уве­личением числа членов полино­ма, для аппроксимации ВАХ обычно используют полиномы низких степеней. Часто для ап­

проксимации ВАХ применяют неполные (укороченные) полиномы, т. е. полиномы, не содержащие членов некоторых степеней. Так, если ВАХ нелинейного элемента проходит через начало координат, то в полиноме (5.14) отсутствует член нулевой степени (а„ ---= 0). Симмет­ричные ВАХ описываются нечетными полиномами, т. е. полиномами, содержащими члены только нечетных степеней.

Аппроксимация с помощью кусочно-линейных функций заключает­ся в разбиении рабочей области аппроксимируемой функции иа не­сколько участков (интервалов) и замене функции на каждом из них отрезком прямой. С увеличением количества интервалов точность ап­проксимации возрастает, однако для упрощения анализа цепи жела­тельно использовать кусочно-линейные функции с минимальным чис­лом интервалов. Примеры кусочно-линейной аппроксимации ВАХ представлены на рис. 5.22.

Аппроксимация вольт-амперных характеристик в окрестности рабочей точки

На практике часто приходится иметь дело с рабочей областью ВАХ настолько узкой, что можно считать, что изменение токов и напряже­ний происходит только в окрестности некоторой рабочей точки. В таких случаях нет необходимости аппроксимировать ВАХ в широком диа­пазоне токов и напряжений, а достаточно ограничиться аппроксима­цией лишь в окрестности выбранной рабочей точки.

Пусть ток и напряжение некоторого нелинейного резистивного элемента в рабочей точке равны i _р и «_р. Значение тока i этого элемента, соответствующее некоторому новому значению напряжения и - и_р -|- -Ь А и, можно представить в виде ряда Тейлора

t = * (“р) + ~ i' (и_Р) ^Ам +^7 Ю (^Ды)² + •••• (⁵-¹⁵)

Здесь i (и_р) — i_p — значение тока в рабочей точке, f (и_р), Г («_р) — значения производных тока по напряжению в рабочей точке, опреде­ляемые либо по заданной функции t ■= i (и), аппроксимирующей ВАХ в широком диапазоне токов и напряжений, либо по табличным значе­ниям, функции ij (Uj) с помощью формул численного дифференциро­вания:

i' (Uj)

М«_/+1)

“/+!'

i"(и ) (“/-О

' («/+>-“;)²

Вводя обозначения а₀ = i (u_p) = t_p; а_г = L i' (ы_р); a₂ i" (u_p);

выражение (5.15) можно представить в виде полинома относительно приращений напряжения

Как правило, при аппроксимации ВАХ нелинейных резистивных элементов в окрестности рабочей точки используются полиномы низ­ких степеней, причем в большинстве случаев, когда приращения на­пряжения А и — и — и_р и тока Аг = i — i_p весьма малы, можно ог­раничиться полиномом первой степени

t = а„ + fliAu. (5.17)

Таким образом, вольт-амперные характеристики нелинейных резистивных элементов могут быть линеаризованы в окрестности выбранной рабочей точки.