§ 5.2. Графические методы анализа

НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ

Простейшие преобразования нелинейных резистивных цепей

Рассмотрим простейшие эквивалентные преобразования, которые можно применять как при анализе нелинейных резистивных цепей постоянного тока, так и при анализе нелинейных цепей, находящих­ся под произвольным внешним воздействием.

Рис. 5.6. Схема участка цепи с последовательно включенными нелинейными сопротивлениями (а) и их ВАХ (б)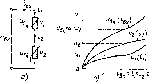

Пусть участок цепи (рис. 5.6, а) содержит два последовательно вклю­ченных нелинейных сопротивления R_x и R₂, вольт-амперные харак­теристики которых представлены на рис. 5.6, б. Очевидно, что при лю­бом значении тока t_BX =

= i_L = i₂ напряжение «_вх на зажимах данного участка цепи равно сум­ме напряжений на каж­дом из нелинейных со­противлений: «ВХ =

~ ^ui (¹х) "Ь ^и2 (¹г)-

Суммируя ординаты шисимостей и_г (i\) и I, (t₂), получаем зависи­мость между напряже- . нем и_вх и током f_BX на сжимах рассматривае­мого участка цепи {рис. 5.6, б). Таким образом, участок цепи, содержащий два последо­вательно включенных нелинейных сопротивления, может быть заменен э{ним нелинейным сопротивлением, ВАХ и_вх (i_BX) которого получается гутем суммирования ординат ВАХ (fj) и и₂(/₂)сопротивлений. Ана- тэтичным образом можно заменить участок цепи, содержащий после­довательно включенные линейное и нелинейное сопротивления, а так- ле участок цепи, представляющий собой последовательное соедине- ■I ie произвольного количества линейных и нелинейных сопротивлений.

• ••••

Пример 5.1. Найдем, зависимость между током и напряжением участка Ч-пи (рис. 5 7, а), представляющего собой последовательное соединение линей- иео R₂ и нелинейного сопротивлений, ВАХ и_г (1_г) и и₂ (i₂) которых приведе­ны на рис. 5.7, б. Определим изменение напряжения Аи₂ на линейном сопротив-

.гении R₂, соответствующее приращению напряжения на зажимах цепи ji_ux на Аи_вх. *

Вольт-амперную характеристику и_вх (i'bx) рассматриваемого участка цепи получаем, суммируя ординаты ВАХ и_х (1_г) и «₂ (i₂) последовательно вклю­ченных элементов. Используя эту характеристику (рис. 5.7, б), можно найти приращение тока цепи Д('_вх, соответствующее изменению входного напряжения на Ди_вх. Далее, используя зависимость и₂ (i.₂), определяем соответствующее

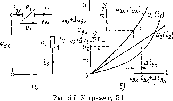
данному приращению тока приращение напряжения Л«₂ на линейном сопротив­лении. Как видно из рис. 5.7, б, приращение напряжения на линейном сопротив­лении оказалось значительно меньше вызвавшего его изменение входного напряже ния Ли_вх.

Рассмотрим участок цепи (рис. 5.8, а), представляющий собой па­раллельное включение двух нелинейных сопротивлений R_x и R₂, ВАХ h (^wi) ^и Н (^ид которых приведены на рис. 5.8, б. Как следует из пер-.

Рис. 5.8. Схема участка цепи с параллельно включенны­ми нелинейными сопротивлениями (а) и их ВАХ (б)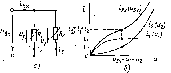

вого закона Кирхгофа, входной ток i_BX рассматриваемого участка це­пи при любом напряжении ы_вх = и_г — и₂ равен сумме токов нелиней­ных сопротивлений: i_nx — t_x (и_г) + t₂ (и₂).

Суммируя ординаты зависимостей t'j («j) и г₂ (и₂). получаем ВАХ ¹вх (ы_Вх) нелинейного сопротивления, которым можно заменить рас­сматриваемый участок цепи. Используя аналогичный прием, можно определить ВАХ участка цепи, содержащего произвольное количест­во параллельно включенных линейных и нелинейных сопротивлений.

Поочередное применение правил эквивалентного преобразования участков с последовательным и параллельным соединением элементов позволяет постепенно «свертывать» участки цепей со смешанным сое­динением линейных и нелинейных сопротивлений с монотонными ВАХ.

• • •••

Пример 5.2. Найдем зависимость между током и напряжением на входе участка цепи со смешанным соединением элементов (рис. 5.9, а). Вольт-ампер- ные характеристики и_г ((,), и.₂ (<₂) и и₃ (i₃) сопротивлений R_lt R₂ и R₃ приве­дены на рис. 5.9, б. Определим приращение напряжения на сопротивлении R₂, соответствующее изменению входного напряжения на Ди_вх.

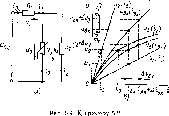
Суммируя абсциссы кривых и_г (i₂) и u₃(i₃), получаем ВАХ ц₂ (/_вх) -- — и j (i_BX) участка цепи, представляющего собой параллельное соединение со­противлений R₂ и R₃. Далее, суммируя ординаты кривых и_г (ij) и и₂ (('вх) = ^{= 11} з (‘вх)г находим зависимость и_вх (i_Sx) на входе рассматриваемого участ­ка цепи.

Пусть напряжение на входе цепи изменилось на Л«_вх. Используя зависимость “вх О'вх,), находим приращение тока Д(_вх> соответствующее этому изменению входного напряжения, и далее с помощью кривой и₂ 0вх5 ^{= и}з (‘вх) определяем приращение напряжения на линейном сопротивлении R„. Как и для цепи, рас­смотренной в примере 5.1, приращение напряжения и₂ оказывается значитель­но меньш им, чем вызвавшее его изменение входного напряжения и_вх.

Цепи, рассмотренные в примерах 5.1 и 5.2, можно использовать для стабилизации напряжения. Отношение относительного прираще­ния напряжения на входе таких цепей к относительному приращению выходного напряжения называется коэффициентом стаби­лизации

и Ди_вХ/и_вх

^ст Л /

^вых/^вых

Очевидно, что для цепи, схема которой приведена на рис. 5.7, а, £ст>1, если ВАХ нелинейного элемента вогнутая [ui (i\) на рис. 5.7, б], а для цепи, схема которой приведена на рис. 5.9, а,— только когда ВАХ нелинейного элемента выпуклая [и₃ (i₃) на

рис. 5.9, б]. Следует подчеркнуть, что эффект стабилизации напряже­ния в принципе не может иметь места в цепях, составленных из эле­ментов с линейными ВАХ.

Преобразования активных нелинейных резистивных двухполюсников

Рассмотрим участок цепи с последовательно соединенными нели­нейным сопротивлением R и источником постоянного напряжения Е_ (рис. 5.10, а). Вольт-амперная характеристика «j (i) нелинейного сопротивления и внешняя характеристика Е_ (t) идеализированного источника напряжения приведены на рис. 5.10, б, в. Очевидно, что на­пряжение на входе такого участка цепи при любом токе равно сумме падения напряжения на сопротивлении и напряжения на зажимах идеализированного источника:

и = (i) + (5.3)

Рис. 5.10. С\ема участка цепи с последовательно соединенны­ми нелинейным сопротивлением и источником постоянной э. д. с. (а), ВАХ нелинейного сопротивления и внешняя харак­теристика источника при Е->0 (б) и £-<0 (в)

^а)

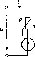
(рис. 5.10, в). Из рис. 5.10, б, в видно, что ВАХ и (i) не проходит че­рез начало координат и частично располагается во втором или четвер­том квадрантах координатной плоскости и—i.

Аналогично ВАХ активного двухполюсника, представляющего со­бой параллельное соединение нелинейного сопротивления R и источ­ника постоянного тока У_ (рис. 5.11, а), получается путем смещения ВАХ tj (и) сопротивления вдоль оси токов на +J- (рис. 5.11, б, в). Как и в предыдущем случае, ВАХ нелинейного двухполюсника, со­держащего источник тока, не проходит через начало координат.

Из выражения (5.3) следует, что ВАХ рассматриваемого участка цепи может быть получена путем суммирования ординат кривых и_у (г) и Е_ (i), т. е. путем смещения ВАХ и_г (i) сопротивления на Е_ вверх по ординате при Е_ > 0 (рис. 5.10,6) или вниз — при £_ < 0

а)

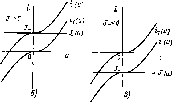
-*ис. 5.11. Схема участка цепи с параллельно соединенными нелинейным сопротив- :гнием и источником постоянного тока (а), ВАХ нелинейного сопротивления и внешняя характеристика источника при 1~ >0 (б) к J <0 (в)

Графические построения можно использовать и при решении об- 'атной задачи: заменить нелинейный двухполюсник, ВАХ которого fe проходит через начало координат, нелинейным сопротивлением и ,'деализированным источником постоянного тока или напряжения.

• ••••

Пример 5.3. Найдем последовательную и параллельную схемы замещения .сточника энергии (рис. 5.12, а), внешняя характеристика и (i) которого при­едена на рис. 5.12, б (штриховая линия).

АД

■ ...Звательная схема замещения рассматриваемого двухполюсника

’.12, в) содержит независимый источник постоянного напряжения Е_ = „ нелинейное сопротивление R_Е, ВАХ которого u_RE (i) (рис. 5.12, б) рается из условия

u_RE (‘) = ^£_— “ (0 = “х— “(О-

Параллельная схема замещения источника энергии содержит независимый .ьпючник постоянного тока J_ = i_H (рис. 5.12, г) и нелинейное сопротивление -?j, ВАХ которого (рис. 5.12, б) определяется из соотношения

Следует обратить внимание на то, что направление тока на зажимах ак­тивного двухполюсника (рис. 5.12, а) выбрано противоположным направле­нию тока, принятого для пассивных двухполюсников, поэтому ВАХ данного двухполюсника переместилась из второго в первый квадрант координатной пло­скости и — i.

Определение рабочих точек нелинейных резистивных элементов

Задача анализа нелинейной цепи постоянного тока обычно сводит­ся к определению рабочих точек нелинейных резистивных эле­ментов, т. е. к определению токов и напряжений на зажимах этих эле­ментов, соответствующих заданным значениям э. д. с. независимых источников постоянного напряжения и токов независимых источни­ков постоянного тока. Эту задачу во многих случаях удобнее решать графически.

Рассмотрим простейшую цепь, состоящую из идеального источни­ка постоянного напряжения £_ и нелинейных сопротивлений R_t и R₂ (рис. 5.13, а), вольт-амперные характеристики которых приведены на рис. 5.13, б [кривые i_x (uj и /₂ (и₂) соответственно]. Для нахождения рабочих точек сопротивлений R_t и R-, воспользуемся методикой пре­образования участка цепи с последовательным соединением нелиней­ных элементов. Суммируя абсциссы кривых («х) и г_а(ы₂), получаем

^а)

Рис. 5.13. Определение рабочих точек нелинейных сопротивлений

ВАХ участка цепи, представляющего собой последовательное соедине­ние сопротивлений R^_ и R₂ [кривая i (ы)]. Используя эту зависимость, находим постоянный ток /_, протекающий через данный участок цепи, а следовательно, и через каждое из сопротивлений, если напря­жение на зажимах этого участка цепи равно напряжению независимо­го источника £_. Далее, используя ВАХ iy («,) и i₂ (и₂) каждого из сопротивлений, определяем падения напряжения на этих сопротивле­ниях t/j_ и U₂_, вызванное током /-. Аналогично можно найти рабо­чие точки произвольного числа последовательно включенных нелиней­ных и линейных сопротивлений, соответствующие различным значени­ям э. д. с. независимого источника постоянного напряжения.

В простейшем случае, когда рассматриваемая цепь содержит только два последовательно включенных сопротивления, а э.д.с. независимо­го источника имеет одно фиксированное значение Е-, для определения рабочих точек сопротивлений можно воспользоваться более простым

фиемом, позволяющим обойтись без построения суммарной ВАХ со- тротивлений. С этой целью на оси напряжений (рис. 5.13, в) отклады- :ают отрезок, соответствующий заданному значению э.д. с. источника ;апряжения, и из конца этого отрезка строят зеркальное отображение ЗАХ одного из элементов, например сопротивления R₂ [кривая ’₂ (£_ — и) на рис. 5.13, в]. В точке пересечения «, (и) и г₂ (£_ — и)

L E./Rz		J4W
1_,	- — у	(^U(E--u)
	у У »
0	и,.	и2- Л и

^а)

Рис. 5.14. Определение рабочей точки нелинейного сопро­тивления с линейной нагрузкой

Рис. 5.15. К примеру 5.4

выполняются условия электрического равновесия цепи /,_ = /₂_ = = /_; и_г- + U₂- -- £-, следовательно, точка пересечения (и) и i₂ (£- — и) и есть искомая рабочая точка нелинейных сопротивле­ний Ri и R₂. Сопротивление R₂, ВАХ которого представляется в виде /₂ (Е- — ^ы). обычно рассматривается как сопротивление на­грузки нелинейного элемента R_lt а кривая t₂ (£_ — и) называется нагру­зочной крива й.

Если одно из сопротивлений, напри­мер R₂. является линейным (рис. 5.14,

2), то задача определения рабочей точки нелинейной цепи с последовательным ;оединением двух сопротивлений упро­щается. В этом случае для определения рабочей точки нелинейного сопротивле­ния R! необходимо найти точку пересе­чения ВАХ ь (и) этого сопротивления с нагрузочной прямой (₂ (£_ — и) = (£_ — u)/R₂, проведенной через точку и = £_ на оси _напряжений и точку i = E-!R_% на оси токов (рис. 5.14, б). Аналогич­ным образом находят рабочие точки управляемых нелинейных ре- з истивных элементов.

• ••••

Пример 5.4. Определим ток стока /_ и напряжение сток—исток U_ полевого транзистора с изолированным затвором, входящего в состав электриче- жой цепи, схема которой приведена на рис. 5.15 (R ■= 2,5 кОм, Е_ = 20 В, л_зи — 1 В). Выходные ВАХ транзистора приведены на рис. 5.4, а.

Рабочая точка транзистора определяется пересечением ВАХ транзистора, мответствующей заданному значению напряжения затвор—исток и_ш = 1 В, и нагрузочной прямой, проведенной через точки Е_ — 20 В на оси напряжения и i = EJR = 8 мА на оси токов (см. рис. 5.4, а). Искомые значения тока сто­ка и напряжения сток—исток /_ — 6,4 мА, II_ = 4 В.

Используя графический метод, можно убедиться, что когда ВАХ нелинейного резистивного элемента монотонна, при каждом значении напряжения источника питания ВАХ элемента пересекается с нагру­зочной прямой только в одной точке, т. е. имеется единственная рабо­чая точка (единственное состояние равновесия).

Немонотонная ВАХ может пересекаться с нагрузочной прямой в нескольких точках (рис. 5.16), и, следовательно, нелинейный резистив­ный элемент с немонотонной ВАХ может иметь несколько рабочих точек (несколько состояний равновесия)¹'¹.

Рис. 5.16. Определение рабочих точек нелинейного сопротивления с немонотонной ВАХ

О

АД

R;

О

^а)

Рнс. 5.17. Применение теоремы об эквивалентном источнике к анализу цепи с одним нелинейным элементом

Если в состав сложной цепи, содержащей произвольное количест­во источников энергии и линейных сопротивлений, входит только один нелинейный элемент, то для определения рабочей точки этого элемента удобно воспользоваться теоремой об эквивалентном источнике. С этой целью нелинейный элемент выделяют из рассматриваемой цепи, а ос­тавшуюся часть цепи представляют в виде линейного автономного двухполюсника АД (рис. 5.17, а). Заменяя этот двухполюсник после­довательной схемой замещения (рис. 5.17, б), сводят задачу анализа сложной цепи к рассмотренной ранее задаче определения рабочей точ­ки нелинейного элемента с линейной нагрузкой (см. рис. 5.14, а).

Определение реакции безынерционного нелинейного резистивного элемента на произвольное внешнее воздействие

Графические методы позволяют определить реакцию произволь­ного безынерционного нелинейного элемента на заданное внешнее воз­действие. Пусть у (х) — ВАХ некоторого нелинейного сопротивления (рис. 5.18, а), причем х—величина, принятая в качестве внешнего воздействия, ay— величина, рассматриваемая как реакция нелиней­ного сопротивления на это воздействие. Построим на этом же рисунке зависимости внешнего воздействия х = х (t) и реакции у = у (t) от

мени. График х (t) расположим в нижней части рисунка так, чтобы х (0 была параллельна оси х ВАХ, а ось времени — направлена °^из. Зависимость у -= у (t) построим в правой части рисунка так, чтобы ось времени была направлена вправо, а ось у (t) расположена

параллельно оси у ВАХ.

Для определения реакции цепи на заданное внешнее воздействие необходимо для каждого момента времени t, выполнить следующие графические построения: по графику функции х (t) найти мгновенное значение внешнего воздействия х (t^, затем по ВАХ определить соот-

Рис. 5.18. Определение реакции безынерционного нелинейного резистивного элемента на заданное внешнее воздействие

нетствукмцее этому внешнему воздействию мгновенное значение реак- |,ин у (ti) и построить точку с ординатой у (t{) на графике у — у (t). Очевидно, что при увеличении количества точек на временной оси, для которых выполняются такие построения, точность определения реак­ции элемента на заданное внешнее воздействие возрастает.

Недостатком рассмотренного приема является то, что графики х (t) и у (t) построены в разных местах чертежа, а это неудобно при определении взаимно соответствующих точек на временных осях и затрудняет сравнение формы кривых х (t) и у (t).

Этот недостаток может быть устранен, если график х (t) построить непосредственно под графиком у (t) (рис. 5.18). В этом случае линии, проектирующие точки графика х — х (t) на ВАХ у {х), перегнутся под углом 90“, причем точки перегиба расположатся на некоторой вспомо­гательной прямой, проведенной под углом 45° к координатным осям через точку пересечения оси у ВАХ и оси времени зависимости х =

I =*(/).

Рис. 5.19. Определение вида ВАХ _п,, известной реакции безынерционного резистивного элемента на заданное виешиее воздействие

Как видно из рисунка, реакции нелинейной цепи иа гармоническое воздействие в общем случае не яв­ляется гармонической функцией вр_е. мени.

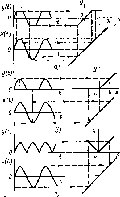
Графические построения, приведенные на рис. 5.18, б, можно использовать и для ре­шения обратной задачи — опре­деления вида ВАХ безынер­ционного нелинейного резистив­ного элемента по известной реакции этого элемента на за­данное внешнее воздействие.

Например, на рис. 5.19 по­казано, как, используя описан­ные графические построения, определить вид ВАХ нелиней­ных резистивных элементов, обеспечивающих двустороннее ограничение гармонических ко­лебаний (рис. 5.19, а), однополупериодное (рис. 5.19,6} и двухполу- периодное (рис. 5.19, в) выпрямление переменного тока.