§ 4.3. Метод сигнальных графов Общие представления о сигнальных графах

Решение уравнения электрического равновесия сложных цепей даже в чис­ленной форме весьма трудоемко. Задача анализа цепи становится особенно слож­ной тогда, когда неизвестные токи и напряжения или комплексные частотные характеристики должны быть найдены в виде аналитических соотношений. В этих случаях весьма полезным может оказаться применение метода сигнальных графов, который позволяет упростить решение уравнений электрического рав­новесия линейных электрических цепей в аналитическом виде (символьной фор­ме).

Как известно, сигнальный граф, или направленный граф про­хождения сигналов, представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. Узлы (вершины) такого графа соответствуют входящим в эту систему неизвест­ным величинам (токам и напряжениям ветвей, контурным токам, узловым на­пряжениям) и величинам, характеризующим внешние воздействия на цепь (то­кам независимых источников тока, э. д. с. независимых источников напряжения, контурным э. д. с., узловым токам). Ветви сигнального графа отображают при­чинно-следственные связи между величинами, соответствующими отдельным уз­лам. В рамках метода сигнальных графов эти величины называются с и г и а­

л ?. м и. Каждой ветви сигнального графа приписывается определенное направление и присваивается весовой коэффициент, который называется передачей ветви. Узлы сигнального графа обозначают темн же буквами, что и соответствующие узлам величины; направления ветвей показы- рают стрелками, около которых указывают передачу ветви.

Если ветвь с передачей А направлена от узла дс_г к узлу Xj (рис. 4.18, а),

то

xj ■- Axi, (4.33)

следовательно, при прохождении через ветвь сигнал умножается на передачу ветви. Разрешим уравнение (4.33) относительно xf.

(4.34)

x_t - xj/A.

Сигнальный граф, соответствующий этому уравнению (рис. 4.18,6), будет отличаться от сигнального графа, соответствующего уравнению (4.33), направ­лением и передачей ветви. Таким образом, вид сигнального графа зависит от того,

-ОХ;

ч°-

Ь)

-oXj

*г°-

а)

1/А

5)

Рис. 4.18. Сигнальные Рис 4.19. Суммирование сигналов в узле

графы, соответствую- сигнального графа

щие выражениям (4.33)

(а) и (4.34) (б)

относительно какой из величин разрешено заданное уравнение, т. е. от того, какая из величин рассматривается как причина, а какая — как следствие.

Если в узле лс* сходится несколько ветвей (рис. 4.19, а), то значение сигна­ла в этом узле будет равно сумме сигналов всех входящих в него ветвей:

N

*kAfciXj, (4.35)

где N — число ветвей, направленных к узлу х*; А^ — передача ветви, направ­ленной от узла xt к узлу х*. Ветви, направленные от узла х*, на сигнал в этом узле не влияют и при подсчете хь не учитываются. В число ветвей, направлен­ных к рассматриваемому узлу, могут входить и ветви, начинающиеся в данном узле (рис. 4.19, б). Такие ветви называются петлями. Значение переменной в узле, к которому подключена одиа или несколько петель, находится по общему правилу (4.35), например (на рис. 4.19,6)

*4 =-- A_nx_t f- А₄2 *2 1- Ац *4- (4.36)

Из выражения (4.36) видно, что при наличии петель, подключенных к ка­кому-либо узлу, переменная, соответствующая этому узлу, входит и в левую, и в правую часть уравнения (4.35).

Рассмотрим некоторые понятия, относящиеся к сигнальным графам.

Истоком называется узел сигнального графа, от которого направлены все примыкающие к нему ветви. Узел сигнального графа, к которому направ­лены все примыкающие к иему ветви, называетси стоком. Узлы, которые имеют как входящие, гак н исходящие ветви, называются смешанными.

Например, в графе (рис. 4.18, д) узел дс* — исток, узел Xj — сток; в графе

(рис. 4.19, б) узлы х_г и х_я — истоки, узел х₃ — сток, узел x_t — смешанный.

Если сигнал, соответствующий некоторому узлу сигнального графа, не выражается через сигналы других узлов, то такой узел является а е з а в и с и- _м ы м. Если сигнал, соответствующий какому-либо узлу, выражается через сигналы других узлов, то такой узел является зависимым. К независимым узлам относятся истоки, к зависимым—стоки и смешанные узлы Очевидно, что уравнения вида (4.35) могут быть составлены только для зависимых узлов.

• ••••

Пример 4.13. В сигнальном графе (рис. 4.20) узлы х_в, x-j — истоки, узел _Хъ .— сток, узлы x_lt х₂, х₃ и x_t относятся к смешанным. Для зависимых узлов %— _№ можно составить систему уравнений

% = ах_г + Ьх₂ + сх₃ + dxt; х₂ — ех₁ + fx₂ + hxi\

*з = gXl,

х₄ = kx_s + mx₃ + nx₂; xb = px_t.

а

Путь между узлами xt и xj сигнального графа — это непрерывная по­следовательность однонаправленных ветвей, связывающая узел х* с узлом xj и проходящая через каждый узел графа не более одного раза. Произведение передач ветвей, образующих путь между узлами Х( и xj, называется переда­чей пути Pji. Так, между узлами и хъ сигнального графа (рис. 4.20) можно указать три пути с передачами Р^У ⁼ dgkp (ветви d, g, k и р), Р^У = = dgmp и Р^³₆> = denp. Последовательность ветвей d. с, т и р не образует пути от вершины хв к вершине хь, так как направление ветви с не совпа­дает с направлением пути.

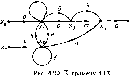
Замкнутый путь, который на­чинается н заканчивается в одном узле, называется контуром.

Очевидно, что петля есть частный вид контура, в который входит одна ветвь. Произведение пере­дач всех ветвей, входящих в /-й контур, называется переда­чей контура Lj. На рис. 4.20 можно выделить четыре контура с передачами L_x = be (ветви Ь и е), L₂ = gc (ветви g и с), L₃ = а (петля а) и L_t — f (петля /). Ветви k и т не образуют контура, так как они не представляют собой замкнутой последовательности однонаправ­ленных ветвей. Такие ветви называются параллельными.

Два контура или контур и путь называются соприкасающимися, если они имеют общие узлы. Если два контура или контур и путь не имеют об­щих узлов, то они являются несоприкасающимися. На рисунке контуры с передачами L₂ = gc и L₄ —/;L₃ = a и /,₄ = / являются иесоприкасаю- щимися, а контуры с передачами = be и L₂ = gc; L± = be и i.₄=/, L_x — = be и L₃ — a — соприкасающимися. Контур с передачей L₄ = / не сопри­касается с путями Р^> и Р^%\ но соприкасается с путем Р$>. Как видно из примера 4.13, каждому сигнальному графу можно однозначным образом поста­вить в соответствие систему линейных алгебраических уравнений, составленных относительно сигналов зависимых узлов.

Для решения обратной задачи — построения сигнального графа, соответст­вующего заданной системе уравнений, эта система уравнений должна быть при­ведена к причинно-следственной форме, т. е. каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различ­ных для каждого из уравнений). Далее, определяется общее число узлов графа N, которое равно сумме числа неизвестных переменных и числа ненулевых сво-

\

\

бодиых членов уравнений. Построение сигнального графа начинается с нанесе­ния точек, соответствующих его узлам. Затем узлы графа, в соответствии с си­стемой уравнений, приведенной к причинно-следственной форме, соединяют­ся между собой ветвями так, чтобы сумма сигналов всех ветвей, сходящихся в каждом узле, равнялась бы значению сигнала этого узла.

Хотя свойства сигнального графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости чертежа, с целью повышения наглядности рекомендуется истоки располагать в левой части черте­жа, стоки — в правой, а остальные узлы — между ними.

В связи с тем что одну н ту же систему уравнений можно различными спо­собами привести к причинно-следственной форме, каждой системе уравнений можно поставить в соответствие некоторое множество графов. Различные гра­фы, соответствующие одной и той же исходной системе уравнений, называются равносильными. Рассмотрим несколько примеров построения графов, соответствующих заданной системе уравнений.

• ••••

Пример 4.14. Построим сигнальный граф, соответствующий системе уравнений

«11*1 + а₁₂х„ + а₁₃х з = Ь_г;

^*21*1 ~"Ь ^22*2 *^2 3*3 ^2>

^31*1 ^ 32*2 **33*3 0.

Приведем данную систему уравнений к причинно-следственной форме, для чего разрешим первое уравнение относительно x_lt второе — относительно х₂, а третье — относительно х₈:

— <*12*2^11 3'^ 3'^/Ql J "Ь ^1^11»

Х₂ ~ 021*1^22 ^a2 3*3^^fl22 ^J^a₂₂,

х₃ = — ^азЛ^^азз &з₂х₂1а₃₃.

^аз,/^азз

~^азг/^азз

Число независимых переменных в этой системе уравнений равно трем, чис­ло ненулевых свободных членов — двум, следовательно, общее число узлов сигналь­ного графа равно пяти. Располагая в левой части чертежа независимые узлы, со­ответствующие свободным, членам b_t и 6₂> ^{а в} правой части узлы, соответствую-

Рис. 4.21. К примеру 4.14

а)

щие неизвестным величинам x_lt х₂, х₃, и соединяя их ветвями в соответствии с системой уравнений, преобразованной к причинно-следственной форме, получим сигнальный граф, изображенный на рис. 4.21, а.

Исходная система уравнений может быть приведена к причинно-следствен­ной форме и другим способом. Прибавляя к правой и левой частям первого урав­нения x_lt второго х_г, третьего х₃ и выполняя преобразования, получим

*1 =/(^аи + О ^Х1 + "12*2 + "13*3 — Ь;

*2 =/“21*1 + («22 + ') *2 + «2 3*3 ~ Ь₂\

X, = а31*! + а32*2 + Озз + 0 Яз-

Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.21, б.

Графы (рис. 4.21, а, б) имеют различную структуру и передачи ветвей, однако они соответствуют одной и той же исходной системе уравнений и по­этому являются равносильными. Очевидно, что если первое уравнение, входящие в исходную систему, разрешить не относительно х_г, а относительно х_г или х₃, то получатся другие варианты представления исходной системы уравнений в причинно-следственной форме, каждому из которых можно поставить в соот­ветствие сигнальные графы, равносильные графам, изображенным на рис. 4.21.

• ••••

Пример 4.15. Составим сигнальный граф, соответствующий узловым урав­нениям цепи, схема которой приведена на рис. 4.2, а.

Узловые уравнения данной цепи были получены при рассмотрении приме­ра 4.4.

Разрешая первое из уравнений относительно U₃₀, а второе — относи­тельно и₂₀, получаем

t/₂₀ = Z₄(l/Z₄+l tz„) и_зв+2₄ J; йзо — ^t (1 /Z-j-f- 1 !Z₃-f- 1 /z_t) 020 — _Z₄ ЁIz%.

Этой системе уравнений соответствует сигнальный гра ф, приведенный на рис. 4.22.

• ••••

Пример 4.16. Используя метод контурных токов, составим систему урав­нений для определения тока /₆ цепи, схема которой приведена на рис. 4.2, а. Построим тако/ве сигнальный граф, соответствующий этой системе уравнений.

-u/lz ^изо -i/z₃

Рис. 4.22, К примеру 4.15 Рис. 4.23. К примеру 4.16

Контурные уравнения рассматриваемой цепи были сформированы при рас­смотрении примера 4.3. Дополняя эти уравнения соотношением, связывающим ток /₆ с контурными токами 1_п и /₂₂, получаем

(£а+^з) /ц —h ^22 ⁼ Ё\

£з ^п + (2з-Ь Z₄+Z») 112—Z^ j;

—J + /"a2 ⁼ 0-

Разрешим каждое из этих уравнений относительно одной из неизвестных величин:

in = (2j +_Zj) /u !Z₃ —E(Z₃; in — (£a"b Z₄-f-Z₆) iilI—Z_e//Z₃;

Ie~J—/ a₄.

Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.23. I

Преобразования сигнальных графов

Используя правила построения сигнальных графов, соответствующих за­данной системе уравнений, можно убедиться, что каждому равносильному пре­образованию исходной системы уравнений соответствует некоторое преобра­зование сигнального графа и, наоборот, каждому преобразованию сигнального графа соответствует определенное преобразование исходной системы уравнений. На практике оказывается, что преобразования сигнальных графов выполняют­ся проще и в более наглядной форме, чем преобразование соответствующих им уравнений. Поэтому при анализе цепей во многих случаях преобразование уравнений электрического равновесия заменяется преобразованием соответст­вующих сигнальных графов

Рис. 4.24. Объедине­ние параллельных ветвей

От

В)

а)

Рис. 4.25. Объединение петель

Рассмотрим основные преобразования сигнальных графов.

Объединение параллельных ветвей. Две параллель­ные ветви с передачами А и В могут быть заменены одной ветвью с передачей А + В. Действительно в соответствии с рис. 4.24, а сигнал в узле, к которому сходятся ветви с передачами А и В, исходящие из узла xt, будет равен

xj= Ах(-\- Вх(, или Х]= (i4+ В) xt-

Последнему уравнению соответствует сигнальный граф, имеющий одну ветвь с передачей А + В, направленную от узла дс_г к узлу xj (рис. 4.24, б). Правило объединения параллельных ветвей обобщается на любое число параллельно включенных ветвей, его можно применять для объединения петель, подключен­ных к одному узлу (рис. 4.25).

Объединение последовательности однонаправленных ветвей. Две последовательно включенные однонаправленные ветви с пере­дачами А и В могут быть заменены одной ветвью с передачей АВ.

Действительно, графу, приведенному на рис. 4.26, а может быть поставле­на в соответствие система уравнений

xj = Ах i;

Xh = Bxj. (4.37)

Исключая из (4.37) переменную Xj, получаем

x_k = ABx_t. (4.38)

Уравнению (4.38) соответствует сигнальный граф, содержащий одиу ветвь с передачей А В (рис. 4.26, б). Рассмотренное преобразование представлиет со­бой частный случай устранения смешанного узла сигнального графа.

Устранение промежуточного узла. Смешанный узел, к которому подключено несколько не образующих контуров ветвей, причем

только одна из ветвей направлена к узлу (рис. 4.27, д) или только одна из вет­

вей направлена от узлаДрис. 4.27, в), называется промежуточным.

Для устранения промежуточного узла первого типа, в которой входит только одна ветвь, составим систему уравнений

х₂ = Axi, x_t = С*₂;

х₃ = Вх₂; *6 = Dx₂

и исключим из нее переменную х₂:

х₃ = АВх_г;

x_t — АСх_г; (4.39)

хь = ADxj.

Системе уравнений (4.39) соответствует граф, не содержащий промежуточ­ного узла х₂ (рис. 4.27, б). Аналогичным образом устраняется промежуточный узел, в который входит несколько ветвей, а выходит только одна (рис. 4.27, г).

А В Х-к

О * о

В)

Рис. 4.26. Объедине- ние последователь-

ности однонаправ- ленных ветвей

Устранение контура. Сигнальному графу, изображенному на рис. 4.28, а, может быть поставлена в соответствие система уравнений

х₂ ■ Ах^ -f- х₃ — Вх₂.

Подставляя первое из этих уравнений во второе, получаем

х₃ = АВх₁ + ВСх₃. (4.40)

Уравнению (4.40) соответствует преобразованный граф, приведенный на рис. 4.28, б.

Исключение петли. Исключение петли с передачей А, подклю- ченной к какому-либо узлу сигнального графа, сопровождается умножением передач ветвей, входящих в этот узел, на 1/(1 — А).

Действительно, для сигнального графа, приведенного на рис. 4.29, а, мож- но составить систему уравнений

дс₃ = Ах_г + Вх ₂ + Сх₃; x_t = Dx₃.

Приводя в первом из этих уравнений подобные члены н разрешая его отно- сительно х₃, получаем

х₃ = Ax_t/(l - С) + BxJ{ 1 - С);

X_L A Xj В X*

о > о- > .. О

а)

X_S

Рис. 4.27. Устранение промежуточного узла, из которого исходит (а, б) ив который вхо­дит (в, г) несколько ветвей

х,<

о)

ВС

АВ

о

5) ^J

А 8/(1-ВС)

V

Рис. 4.28. Устранение конту­ра

Как видно из соответствующего системе уравнений (4.41) сигнального гра­фа (рис. 4.29, б), после устранения петли передачи ветвей, входящих в узел х₃, оказались умноженными на 1/(1 — С), а передача ветви, выходящей из узла х₃, осталась без изменения.

-П/А

Рис. 4.30. Ииверсня ветвн

Применяя операцию устранения петли, преобразованный граф (см. рис. 4.28, б) можно заменить одной ветвью (см. рис. 4.28, в).

Инверсия (изменение направления) ветви. Рас­смотрим некоторый граф (рис. 4.30, а), которому соответствует система урав­нений

дс₄ = Ах_г + Вх ₂ + Сх₃ + Dx_t\ хь = Ех₄. (4.42)

• X

к"*³

⁸\*2

в;

/ ^г)

Рис. 4.31. Расщепление узла

Системе уравнении (4.43) соот­ветствует сигнальный граф, изобра­женный на рис. 4.30, б. Как видно из сравнения рис. 4.30, а и б, инвер-

Пусть необходимо изменить на­правление какой-либо ветви, напри­мер, направленной из вершины % в вершину х₄. С этой целью разре­шим первое из уравнений (4.42) от­носительно

О

хъ E_Xi. (4.43)

Рис. 4.32. Удлинение узла

*i — А — BxJA—Cx^lA — Dx_t'A;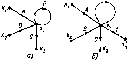

тирование ветви, направленной от узла xi к узлу Xj, сопровождается измене­нием передач и точек подключения всех ветвей, ранее направленных к узлу xj. Ветвь с передачей А, направленная от узла xj к узлу xj, заменяется ветвью, направленной от узла xj к узлу с передачей и А. Все ветви, ранее направ­ленные к узлу Xj, заменяются ветвями, направленными к узлу xt, передачи этих ветвей умножаются на —1/А, Ветви, не направленные ранее к узлу xj, при инвертировании ветви, направленной к Xj, остаются без изменений.

Расщепление узла. В связи с тем что сигнал в каждом узле сиг­нального графа определяется только сигналами входящих в него ветвей, любой узел сигнального графа может быть расщеплен на два узла: один — содержа­щий все ветви, направленные к узлу, другой — направленные от узла. Так, узел л:* графа, изображенного на рис. 4.31, а, может быть расщеплен на две узла (рис. 4.31, б). Узел, который содержит только исходящие из него ветви (исток), может быть расщеплен на произвольное количество узлов, не превы­шающее числа исходящих из него ветвей (рис. 4.31, я).

Удлинение узла. В ряде случае возникает необходимость вб вве­дении в сигнальный граф дополнительного узла, сигнал в котором совпадает с сигналом в одном из узлов Xj сигнального графа. Такая операция называется удлинением узла хj. Для удлинения узла xj этот узел должен быть соединен с вновь вводимым узлом х/ ветвью, передача которой равна единице, Например,

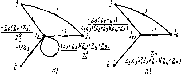
для удлинения узла х₄ (рис. 4.32, а) введем новый узел x'_t и соединим его с уз­лом x_t ветвью, передача которой равна единице (рис. 4.32, б).

Совместное проведение описанных преобразований позволяет, как правило, существенно упростить структуру сигнального графа. Конечной целью преобра­зований обычно является получение наиболее простого графа, не допускающего дальнейших упрощений. Такой граф называется конечным. Конечный граф не содержит смешанных узлов, а включает в себя только стоки и истоки.

• ••••

Пример 4.17. Упростим сигнальный граф, изображенный на рис. 4.23. Для этого последовательно исключим контур (рис. 4.33, а), петлю (рис. 4.33, б), промежуточный узел (рис. 4.33, в) и объединим параллельные ветви (рис. 4.33,г). Преобразованный граф, (рис. 4.33, г) не содержит смешанных узлов и не подлежит дальнейшему упрощению. Этот граф является конечным.

Применение сигнальных графов к анализу цепей

Применение метода сигнальных графов при анализе цепей оказывается весьма эффективным в тех случаях, когда требуется определить ток или напря­жение только одной из ветвей цепи, а также найти ее комплексные частотные характеристики.

Как отмечалось, используя различные преобразования, исходный сигналь­ный граф можно привести к конечному. Если истоками графа являются узлы, сигналы которых X; есть комплексные изображения величин, характеризующих внешние воздействия на зажимах i—Г, а стоками — узлы, сигналы которых Yj представляют собой комплексные изображения искомых токов или напря­жений ветвей, подключенных к зажимам /—то, используя конечный граф, можно записать соотношения, в явной форме выражающие зависимость иско­мых неизвестных токов и напряжений от величин, характеризующих внешние воздействия. Передача ветви Aji конечного графа, связывающей исток Х_г со

стоком Yj, будет равна комплексной частотной характеристике цепи Нц (jto), измеренной в режиме, когда все источники внешнего воздействия, за исключе­нием Х_;, выключены.

Трудоемкость преобразования сигнального графа к конечному во многом определяется выбором исходной системы уравнений электрического равнове­сия и тем, каким образом осуществлен переход от исходной системы уравнений к сигнальному графу. Для уменьшения числа узлов сигнального графа в каче­стве исходной системы уравнений рекомендуется применять систему уравнений электрического равновесия цепи, составленную по методу узловых напряжений или контурных токов, дополнив ее уравнениями, связывающими искомые токи и напряжения с контурными токами или узловыми напряжениями.

• ••••

Пример 4.18. Определим ток Ц цепи, комплексная схема замещения кото­рой приведена на рис. 4.2, а, преобразуя сигнальный граф этой цепи (см. рис. 4.23) в конечный.

Граф, приведенный на рис. 4.23, соответствует контурным уравнениям рассматриваемой цепи, дополненным уравнением, выражающим связь искомого тока с контурными токами /_п, /._« и /₃₃= J (см. пример 4.16). Преобразование этого графа в конечный было проведено в примере 4.17. Непосредственно по виду конечного графа записываем выражение для искомого тока

— {1^2_2з (£г + 2з)1 J 2з Ё) !\2._гЪ₃ (/-2 + Z₃) (Zf-\-Zg)] >

которое совпадает с выражениями для этого тока, подученными с использова­нием метода наложения (см. пример 4.8) и теоремы об эквивалентном источни­ке (см. пример 4.12).

Передача ветви, связывающей исток J и сток /₆, равна комплексному коэф­фициенту передачи цепи по току G_№ (ju>) от зажимов 5—5' к зажимам 6—6' (номера зажимов совпадают с номерами ветвей) в режиме, когда источник Ё закорочен:

■Z

₂ Z₃ -\-Z₄ (Z2+Z3)

°65 (/®) =

я= о Z_SZ₃4-(Z_S + Z₃) (Z₄+Z_e)

—

Передача ветви, направленной от истока Е к стоку h, равна передаточ­ной проводимости цепи Y_ei (/со) в режиме, когда ветвь с источником тока J разомкнута:

у=о Z₃-|-(Z₂-|-Z₃) (Z₄4-Z₆)

Уел (/®) =•—

Ui

Следует отметить, что сведение исходного сигнального графа к конечному, особенно для сложных цепей, может оказаться трудоемким. Кроме того, если необходимо определить несколько неизвестных величин, эту процедуру прихо­дится выполнять несколько раз. Поэтому в таких случаях для нахождения ком­плексных частотных характеристик цепи и неизвестных токов и напряжений це­лесообразно воспользоваться формулой Мейсона, которая позволя­ет вычислять передачи ветвей конечного графа Aji= Нр (/со) непосредствен­но по исходному сигнальному графу, не прибегая к его преобразованиям.

Формула Мейсона имеет вид

Aji = _Hji (/со) = ^ ^Pf ^Д*] j ^Д. (4.44)

где Д — определитель сигнального графа, численно равный определителю ис­ходной системы уравнений; Р*** ■— передача k-ro пути от истока X* к стоку У у, Д* — алгебраическое дополнение й-го пути. Суммирование производится по всем возможным путям нз узла Xj в узел Y j.

Определитель сигнального графа

А = 1 • 1 (4.45)

i ij t.i.m

где 2 Li—сумма передач всех контуров сигнального графа; 2 LiLj — сумма

¹ t,i

произведений передач всех возможных пар несоприкасающихся контуров; 2 LiLjL_m—сумма произведений передач всех несоприкасающихся троек кон- t,j,m

туров и т. д. Алгебраическое дополнение k-ro пути также вычисляется по форму­ле (4.45), но при этом учитываютси только контуры, не касающиеся пути Р^}.

• ••••

Пример 4.19. Используя формулу Мейсона, определим передаточную про­водимость Yei (/со) цепи, схема которой приведена на рис. 4.2, а).

Сигнальный граф, составленный с использованием контурных уравнений цепи, был приведен на рис. 4.23 (см. пример 4.16). Этот граф содержит един­ственный контур, передача которого

i = (2₂ + Z₃) (Z₃+Z4-(-Z5)/(Z|).

Используя выражение (4.45), найдем определитель сигнального графа ^ ^ (2* + 2з) (£₃-b2₄+Z_e) Z% Zr3~\~(Z₂ -\-Z₃) (Z₄+_Z_e)

Между узлами Е и }_в существует единственный путь, проходящий по вет­вям с передачами —1/Z₃ и —1. Передача этого пути Р^_еу = 1 IZ₃. Единственные?

контур сигнального графа имеет общую вершину /₂₂ с данным путем, поэтому Д_х = 1.

Подставляя полученные значения Р^, А и Д_х в формулу Мейсона, получаем

Y_n (/ш)

—*—Z₃/[Z₂ Z₃-|- (Zp-^-Zg) (Z₄-j~Z₆)]. /=о ~

Как и следовало ожидать, это выражение совпадает с выражениями для У_Й1 ( у со), полученными другими методами (см. примеры 4.8, 4.12, 4.18).

• ••••

Пример 4.20. Используя формулу Мейсона, определим комплексный ко- эффициент передачи по току G_St (]'а>)'цепи, схема которой приведена на рис. 4.2, а.

Сигнальный граф рассматриваемой цепи изображен на рис. 4.23. Выраже­ние для определителя Д этого графа было получено в примере 4.19.

Между узлами J и 1_в существуют два пути с передачами

^Р^5^{)==1; я}Р_в⁾⁼=£о £.+£>/£!•

Алгебраическое дополнение первого пути

j (^2+^3) (Z₃-|-Z₄ + Z_e) Z₂_Z₈+(Z₂+Z₃) (Z₄+Z,) ^

_i=1 __ ₌ __ „

Алгебраическое дополнение второго пути равно единице. Используя формулу Мейсона, находим

_г .. . Л./ ^5^)Д 1+^5 Z.Z. + Z.i^ + Z,)

^65 (/®) —

J I Ё—0 Д Zg Z3 + (Zj + Zg) (Z₄+Z_e)

Нетрудно убедиться, что полученное выражение совпадает с выражениями для G_e6 0'w), найденными другими методами (см. примеры 4.8, 4.12, 4.18).

Нелинейные резистивные цепи