Пример 2.10. Рассчитать и построить механическую характеристику электродвигателя. Определить фактическое и допустимое число пусков привода в час

Критическое скольжение, соответствующее максимальному вращающему моменту электродвигателя определяем по формуле

где m₁ – коэффициент, равный отношению кратности максимального и кратности пускового моментов:

Синхронная частота

Номинальное скольжение электродвигателя

Параметр q может быть определен по соотношению

Механическая характеристика электродвигателя М_д (ω) рассчитывается по формуле Клосса:

где s – текущее скольжение;

Время разбега и торможения системы под нагрузкой и на холостом ходу может быть определено на основе уравнения движения электропривода

где М_изб – избыточный момент системы, Нм.

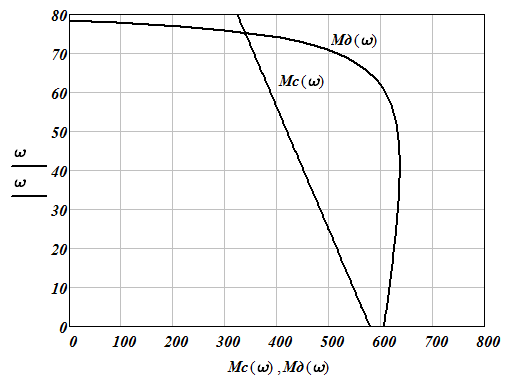
Рисунок 5. Механическая характеристика двигателя М_д(ω) и механическая характеристика момента сопротивления М_с(ω).

Время полного разбега и время торможения возьмем из пункта 2

При повторно–кратковременном режиме электродвигатель сильно нагревается из-за повышенных потерь в период пуска. Чтобы это предотвратить, необходимо выполнить условие

где h – число включений электродвигателя в час;

h_доп – допустимое число включений электродвигателя в час.

Число включений электродвигателя в час, h определяется по формуле

где t_p и t₀ – соответственно продолжительность работы и паузы, мин.

Допустимое число включений электродвигателя в час, исходя из условий допустимого нагревания, рассчитывается по формуле

где ΔР_н – номинальные электрические потери мощности электродвигателя, Вт; А_н – потери энергии при пуске электродвигателя, Дж., β_о - коэффициент ухудшения теплоотдачи, принимаем для самовентилируемых двигателей 0.55;

Номинальные электрические потери мощности электродвигателя

где α – коэффициент, равный отношению постоянных потерь мощности электродвигателя к переменным (α = 0,5 – 0,6);

η_н - КПД двигателя при номинальной нагрузке, примем 0.83.

Потери энергии при пуске электродвигателя ΔА_п

где i_п – кратность пускового тока электродвигателя, для асинхронного двигателя с фазным ротором принимаем равным 2.

Вывод: по результатам расчета число допустимых включений в час равно фактическому числу включений в час, следовательно электродвигатели не будут перегреваться.

6.1 Исследование в динамических режимов работы эп

6.1.1 Математическая модель привода. Для определения характера прохождения переходных процессов системы в переходных режимах необходимо определить коэффициенты характеристического уравнения системы в операторной форме:

, (5.1)

где Т_М – механическая постоянная времени системы, Т_Э – электромагнитная постоянная времени;

Определить постоянные времени можно с помощью следующих выражений:

(с); (5.2)

(с), (5.3)

где (рад/с).

(с), ,

а это значит, что переходные процессы в системе должны иметь колебательный характер.

6.2. Выбор модели и моделирование переходных процессов. Для моделирования ЭП используется система MatLab (матрич­ная лаборатория) с расширением (Toolboxes). Основными пакетами расширения, используемыми для исследовании ЭП, являются Simulink и Power System Blockset.

В исследуемую модель (рис. 5.1) вошли такие элементы:

• Asynchronous Machine SI Unit – модель асинхронного двигателя с номинальными паспортными данными двигателя АМУ 160 М6 Т2;

• 3 источника синусоидального напряжения AC Voltage Sourse с номинальными параметрами: f=50 Гц, U_m=311 В; сдвинутые по фазе друг относительно друга на 120⁰.

• Three-Phase V-I Measurement – трехфазный мультиметр для замеров сетевого тока и напряжения.

• 2 элемента типа Scope – модели осциллографов для просмотра графиков сетевых тока и напряжения, а также изменения во времени частоты вращения ротора двигателя и момента на его валу.

• 2 элемента типа Display для контроля установившегося значения тех же параметров.

• Step – элемент, с помощью которого, возможно смоделировать наброс нагрузки на вал двигателя в определенный момент времени.

Рис.5.1. Модель системы ПЧ-АД для программного пакета MatLab

Моделируем пуск двигателя без нагрузки при трех различных частотах питающего напряжения f₁=50 Гц, f₂=37,5 Гц, f₃=25 Гц, используя закон частотного регулирования .

При f=50 Гц U_л=380 В; при f=37,5 Гц U_л=329 В; при f=25 Гц U_л=269 В.

При частоте питающей сети f=50 Гц и линейном напряжении U_л=380 В получаем следующие графики переходных процессов ω=f(t) (рад/с) и M_в=f(t) (Н·м).

Рис. 5.2. Графики ω=f(t) и M_в=f(t) при f=50 Гц

После окончания переходного процесса получаем такие установившиеся значения:

ω =104,7 рад/с; I₁=7,266 А; M_в=0,517 Н·м

При частоте питающей сети f=37,5 Гц и линейном напряжении U_л=329 В получаем следующие графики переходных процессов ω = f(t) (рад/с) и Mв = f(t) (Н·м).

Рис. 5.3. Графики ω=f(t) и M_в=f(t) при f=37,5 Гц

После окончания переходного процесса получаем такие установившиеся значения: ω =78,53 рад/с; I₁=7,608 А; M_в=0,3883 Н·м

При частоте питающей сети f=25 Гц и линейном напряжении U_л=269 В получаем следующие графики переходных процессов ω=f(t) (рад/с) и M_в=f(t) (Н·м).

Рис. 5.4. Графики ω=f(t) и M_в=f(t) при f=25 Гц

После окончания переходного процесса получаем такие установившиеся значения: ω =52,36 рад/с; I₁=10,29 А; M_в=0,036 Н·м

При частоте питающей сети f=50 Гц и линейном напряжении U_л=380 В смоделируем переход системы из одного установившегося состояния (М_в = М_н = 73 Н·м, ω = ω_н = 101.7 рад/с, I₁ = I_1н = 15,65 А) в другое после наброса нагрузки на вал двигателя (М_с.доп.= 0,3М_н = 22 Н·м).

Рис. 5.5. Наброс нагрузки М_с.доп.=0,3М_н

После окончания переходного процесса получаем такие установившиеся значения: ω =99,7 рад/с; I₁=20,06 А; M_в=95,5 Н·м

Для более детального изучения переходного процесса на рис. 5.6. приведена увеличенная часть графиков ω=f(t) (рад/с) и M_в=f(t) (Н·м), охватывающая только момент замедления двигателя после наброса дополнительной нагрузки.

Рис. 5.5. Наброс нагрузки М_с.доп.=0,3М_н (фрагмент)