Уравнение вида:

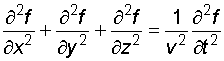                                                                                                                                  (2.5)

представляет собой волновое уравнение. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при  , дает фазовую скорость этой волны. Вид функции может быть любым, в частности, ее можно выбрать и гармонической. Это особенно удобно, так как многие физические устройства регистрируют поля, гармонически изменяющиеся со временем. Кроме того, по теореме Фурье любая физически реализуемая функция может быть выражена через совокупность гармонических функций с определенными частотами, амплитудами и начальными фазами.

Уравнения (2.3) и (2.4) – волновые уравнения для векторов   и   соответственно. Всякая функция, удовлетворяющая уравнениям (2.3) и (2.4), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн, фазовая скорость которых

.

Для вакуума по этой формуле получается

.

Таким образом, в вакууме фазовая скорость электромагнитных волн совпадает со скоростью света.

Из уравнений (2.3) и (2.4) следует, что электромагнитные волны могут распространяться и в вакууме.

Электромагнитные волны – это поперечные волны: векторы   и   напряженностей электрического и магнитного полей волны лежат в плоскости, перпендикулярной к направлению распространения волны, т. е. к вектору ее скорости   в рассматриваемой точке поля.

Векторы   и   поля электромагнитной волны взаимно перпендикулярны, так что  ,   и   образуют правую тройку векторов.

Из уравнений Максвелла следует также, что в электромагнитной волне векторы   и   всегда колеблются в одной фазе – они одновременно обращаются в ноль и одновременно достигают максимальных значений.  Модули их связаны соотношением:  , справедливым для любой бегущей электромагнитной волы. В вакууме это соотношение выглядит:  .

Важным следствием из уравнений электродинамики является вывод о том, что электромагнитное поле, возникнув около зарядов, движущихся с ускорением, в дальнейшем может существовать независимо от них, распространяясь в пространстве со скоростью света. Это свойство электромагнитного поля позволило окончательно расстаться с идеей существования гипотетического эфира как некоторой светоносной среды, обладающей весьма противоречивыми свойствами. Для электромагнитных волн не нужно никакой среды, они сами являются наряду с веществом одним из видов материи.

Скорость света не зависит от скорости источника света и является инвариантом при переходе от одной инерциальной системы отсчета к другой. Этот физический факт хорошо согласуется с уравнениями Максвелла, которые были сформулированы задолго до создания специальной теории относительности. Система уравнений Максвелла оказалась инвариантной к преобразованиям Лоренца. Таким образом, скорость света в вакууме является фундаментальной константой и определяет максимальную скорость передачи взаимодействий в природе.

 

§ 2. Уравнение полоской и сферической волн

 

Волновые процессы представляют собой общий класс явлений.  Несмотря на бесконечное разнообразие физических процессов, вызывающих волны, образование волн происходит по одному общему типу. Возмущение, происшедшее в какой-нибудь точке в известный момент времени, проявляется спустя некоторое время на некотором расстоянии от начальной точки, т. е. передается с определенной скоростью. Рассмотрим самый простой пространственно одномерный случай: распространение возмущения вдоль оси ОХ. Тогда можно изобразить возмущение f как функцию координаты x и времени t,  . Распространение возмущения со скоростью  вдоль направления ОХ изобразится той же функцией, в аргумент которой t и x входят в комбинации   или   в зависимости от направления распространения возмущения вдоль оси ОХ.

В этом случае волновое уравнение (2.5) имеет вид:

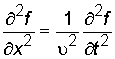                                          ,                                                                                                           (2.6)

а его общее решение выглядит

.                                                                                               (2.7)

Если в начальный момент времени t = 0 графически изобразить функции ₁(x) и ₂(x), то в последующие моменты времени эти функции будут смещаться вдоль оси ОХ со скоростью  как целое: ₁ – вправо, ₂ – влево.

Рассмотрим гармонические монохроматические волны, т. е. синусоидальные волны с одной циклической частотой  = 2.

В этом случае зависимость любой величины f от времени t в общем виде выглядит так:

 

,

 

где f₀ – значение рассматриваемой величины в точке с координатой x в начальный момент времени t = 0. Решение волнового уравнения (2.6), удовлетворяющее условию (2.7) и дающее гармоническую зависимость f от t, имеет вид:

.                                                                                                    (2.8)

Выражением 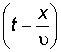  в формуле (2.8) определяется фаза волны (ее состояние в данный момент времени в данной точке пространства). В данный момент времени волновой фронт – геометрическое место точек, в которых фаза колебаний имеет одно и то же значение – описывается уравнением x = const. Это плоскость, нормальная к оси OX и перпендикулярная направлению распространения волны. Таким образом, волновой фронт распространяется вправо с фазовой скоростью . Так как волновой фронт является плоскостью, мы получили плоскую волну. Нам необходимо также выражение для плоской волны, распространяющейся в произвольном направлении, характеризуемом постоянным единичным вектором  . Так как уравнение плоскости, перпендикулярной вектору  , имеет вид   = const, уравнение плоской волны можно записать в виде:

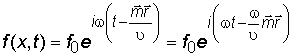.                                                                                      (2.9)

Электромагнитные волны представляют собой распространение электромагнитных полей в пространстве и времени.

Деление электромагнитного поля на электрическое и магнитное зависит от выбора системы отсчета. Действительно, вокруг зарядов, покоящихся в одной системе отсчета, существует только электрическое поле; однако эти же заряды будут двигаться относительно другой системы отсчета и порождать в этой системе отсчета, кроме электрического, еще и магнитное поле. Таким образом, теория Максвелла связала воедино электрические и магнитные явления.

- всякое изменение электрического поля возбуждает в окружающем пространстве вихревое магнитное поле, линии индукции которого расположены в плоскости, перпендикулярной линиям напряженности переменного электрического поля, и охватывают их (рис.2б).Линии индукции возникающего магнитного поля образуют с вектором «правый винт». Такие волны могут распространяться не только в газах, жидкостях и твердых средах, но и в вакууме.Скорость электромагнитных волн в вакууме с=300000 км/с. Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.Распространение электромагнитной волны в диэлектрике представляет собой непрерывное поглощение и переизлучение электромагнитной энергии электронами и ионами вещества, совершающими вынужденные колебания в переменном электрическом поле волны. При этом в диэлектрике происходит уменьшение скорости волны.Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии. Если выделить площадку S (рис. 4), ориентированную перпендикулярно направлению распространения волны, то за малое время Дt через площадку протечет энергия ДWэм, равная

ДWэм = (wэ + wм)хSДt.

При переходе из одной среды в другую частота волны не изменяется.Электромагнитные волны могут поглощаться веществом. Это обусловлено резонансным поглощением энергии заряженными частицами вещества. Если собственная частота колебаний частиц диэлектрика сильно отличается от частоты электромагнитной волны, поглощение происходит слабо, и среда становится прозрачной для электромагнитной волны.Попадая на границу раздела двух сред, часть волны отражается, а часть проходит в другую среду, преломляясь. Если второй средой является металл, то прошедшая во вторую среду волна быстро затухает, а большая часть энергии (особенно у низкочастотных колебаний) отражается в первую среду (металлы являются непрозрачными для электромагнитных волн).Распространяясь в средах, электромагнитные волны, как и всякие другие волны, могут испытывать преломление и отражение на границе раздела сред, дисперсию, поглощение, интерференцию; при распространении в неоднородных средах наблюдаются дифракция волн, рассеяние волн и другие явления.Из теории Максвелла следует, что электромагнитные волны должны оказывать давление на поглощающее или отражающее тело. Давление электромагнитного излучения объясняется тем, что под действием электрического поля волны в веществе возникают слабые токи, то есть упорядоченное движение заряженных частиц. На эти токи действует сила Ампера со стороны магнитного поля волны, направленная в толщу вещества. Эта сила и создает результирующее давление. Обычно давление электромагнитного излучения ничтожно мало. Так, например, давление солнечного излучения, приходящего на Землю, на абсолютно поглощающую поверхность составляет примерно 5 мкПа.