
Вопросы для экспресс контроля.
Какой газ называется идеальным? Опишите атомно-молекулярную модель идеального газа.
Что такое средняя квадратичная скорость молекул?
Приведите и поясните основное уравнение молекулярно-кинетической теории идеального газ.
В чем смысл абсолютной температуры с точки зрения молекулярно – кинетической теории.
Какие явления называются явлениями переноса? Какие явления переноса вы знаете?
Что такое диффузия? В чем заключается закон Фика?
Что такое теплопроводность? Сформулируйте закон Фурье.
Дайте понятие вязкости. Сформулируйте закон Ньютона для вязкости.
Как зависят коэффициенты диффузии, вязкости и теплопроводности от давления и температуры идеального газа?
Как связаны между собой коэффициенты диффузии, вязкости и теплопроводности идеального газа?
Найти молярную массу и число степеней свободы молекул газа, если известны его удельные теплоемкости:
 Дж/(гК) и
Дж/(гК) и
 Дж/(гК).
Дж/(гК).Теплоизолированный сосуд с газообразным азотом при температуре
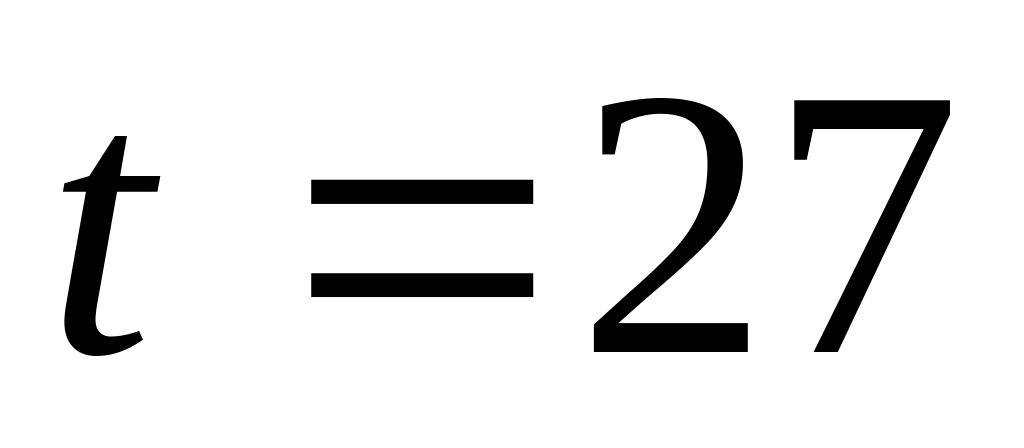 0С
движется со скоростью
0С
движется со скоростью
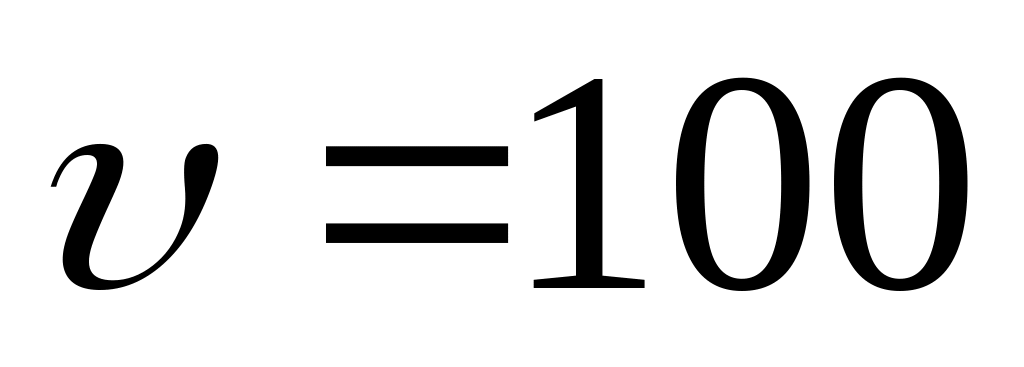 м/с. Как и на сколько процентов изменится
давление газа после внезапной остановки
сосуда?
м/с. Как и на сколько процентов изменится
давление газа после внезапной остановки
сосуда?*Во сколько раз надо расширить адиабатически газ, состоящий из жестких двухатомных молекул, чтобы их средняя квадратичная скорость уменьшилась в
 раза?
раза?Газ из жестких двухатомных молекул, находившийся при нормальных условиях, адиабатически сжали в
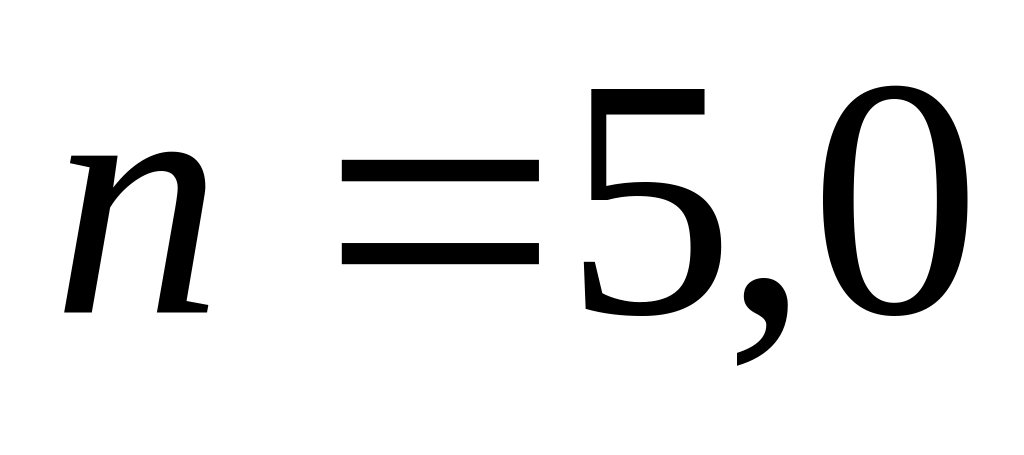 раза по объему. Найти среднюю кинетическую
энергию вращательного движения молекулы
в конечном состоянии.
раза по объему. Найти среднюю кинетическую
энергию вращательного движения молекулы
в конечном состоянии.Найти среднюю длину свободного пробега и среднее время между столкновениями молекул газообразного азота, находящегося:
при нормальных условиях;
при температуре
 0С
и давлении
0С
и давлении
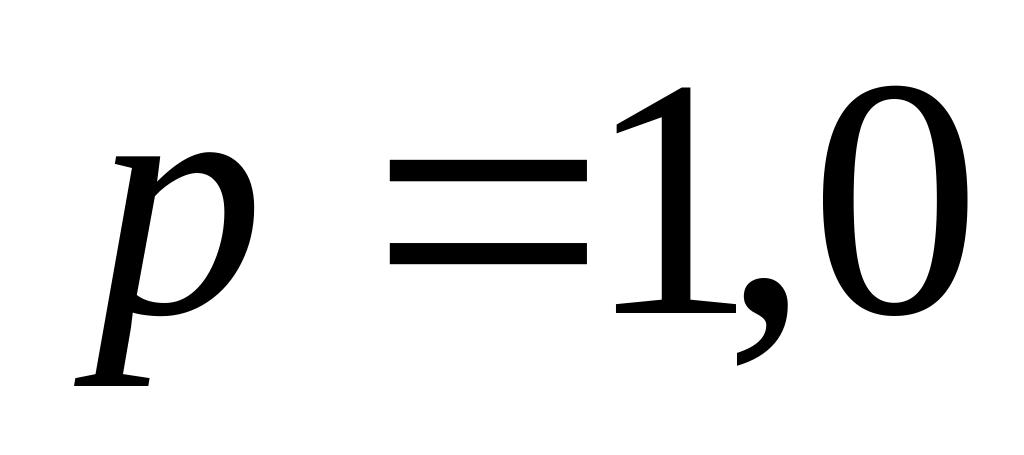 нПа (такое давление позволяют получать
современные насосы)?
нПа (такое давление позволяют получать
современные насосы)?
Идеальный газ совершает политропический процесс с показателем политропы . Найти среднюю длину свободного пробега и число столкновений каждой молекулы ежесекундно как функцию:
объема V;
давления P;
температуры Т;
*Идеальный газ с молярной массой находится в тонкостенном сосуде объемом
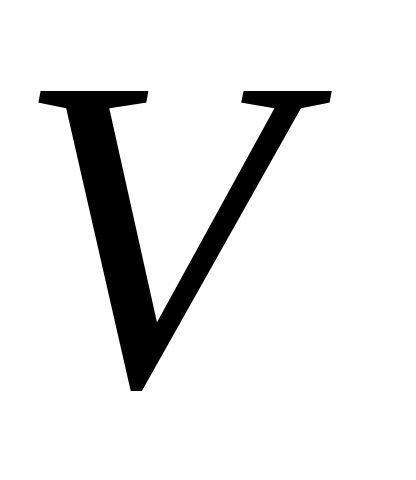 ,
стенки которого поддерживаются при
постоянной температуре
,
стенки которого поддерживаются при
постоянной температуре
 .
В момент времени
.
В момент времени
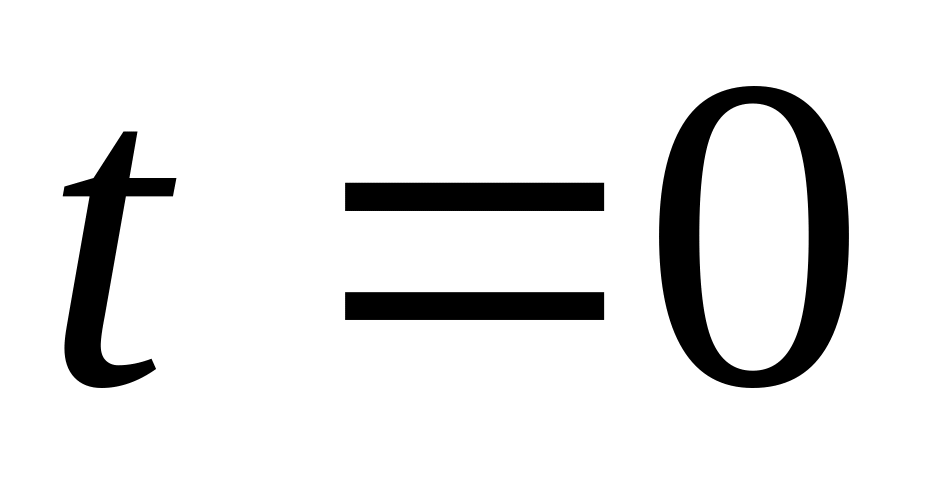 в стенке сосуда открыли малое отверстие
площадью S,
и газ начал вытекать в вакуум. Найти
концентрацию
газа как функцию времени
в стенке сосуда открыли малое отверстие
площадью S,
и газ начал вытекать в вакуум. Найти
концентрацию
газа как функцию времени
 ,
если в начальный момент времени
,
если в начальный момент времени
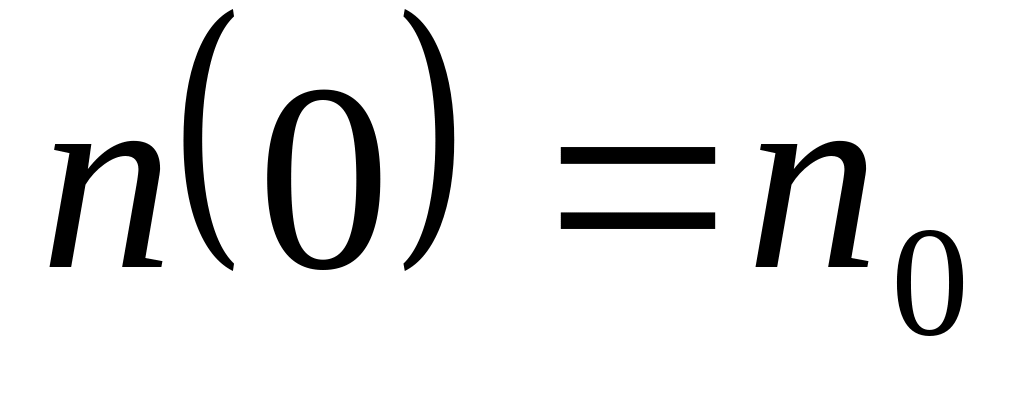 .
.
В результате некоторого процесса коэффициент вязкости идеального газа увеличился в
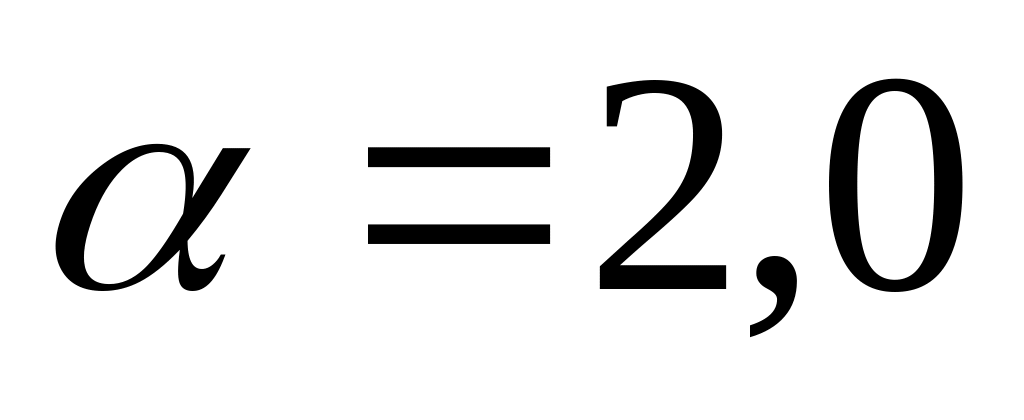 раза, а коэффициент диффузии – в
раза, а коэффициент диффузии – в
 раза. Как и во сколько раз изменилось
давление газа?
раза. Как и во сколько раз изменилось
давление газа?Найти показатель политропы процесса, совершаемого идеальным газом, при котором остается неизменным коэффициент: а) диффузии; б) вязкости; в) теплопроводности.
Газ заполняет пространство между двумя длинными коаксильными цилиндрами, радиусы которых
 и
и
 ,
причем
,
причем
 .
Внутренний цилиндр неподвижен, а
внешний вращают с достаточно малой
угловой скоростью
.
Внутренний цилиндр неподвижен, а
внешний вращают с достаточно малой
угловой скоростью
 .
Момент сил трения, действующих на
единицу длину внутреннего цилиндра
равен
.
Момент сил трения, действующих на
единицу длину внутреннего цилиндра
равен
 .
Найти коэффициент вязкости газа
.
.
Найти коэффициент вязкости газа
.*Найти распределение температуры в пространстве между двумя коаксильными цилиндрами с радиусами
 и
и
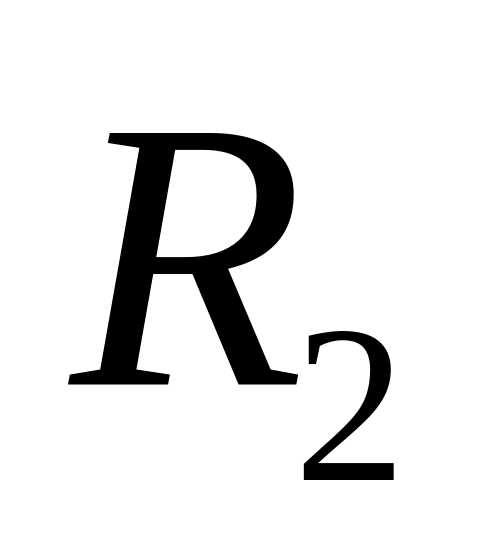 ,
заполненном однородным теплопроводящим
веществом, если температуры цилиндров
постоянны и равны соответственно
,
заполненном однородным теплопроводящим
веществом, если температуры цилиндров
постоянны и равны соответственно
 и
и
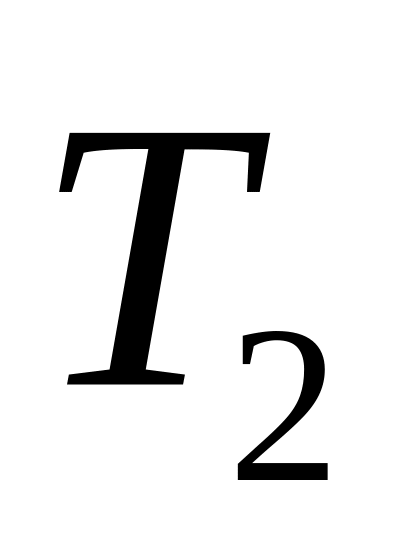 .
.Определить толщину льда, образующегося в течении заданного времени на спокойной поверхности озера. Считать, что температура Т окружающего воздуха все время постоянна и равна температуре наружной поверхности льда (Т<Тпл, где Тпл – температура плавления льда). Произвести численный расчет, предполагая, что Т=263 К. Для льда коэффициент теплопроводности равен 2,22 Дж/(с·м·К), удельная теплота плавления льда
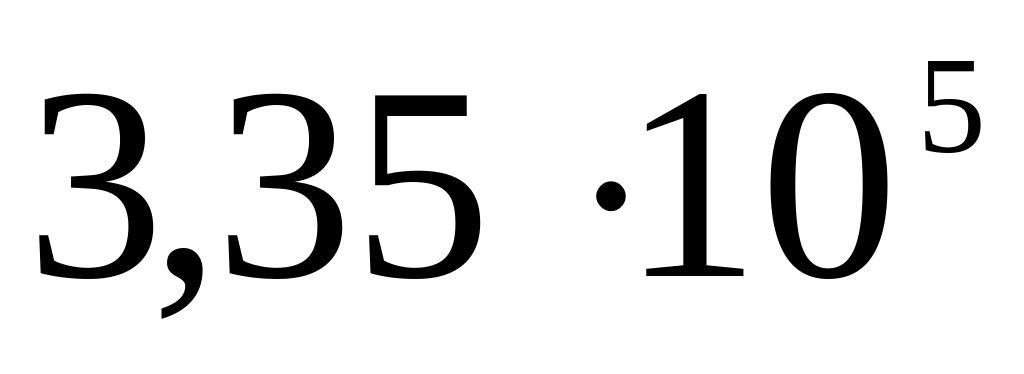 Дж/кг, плотность
Дж/кг, плотность
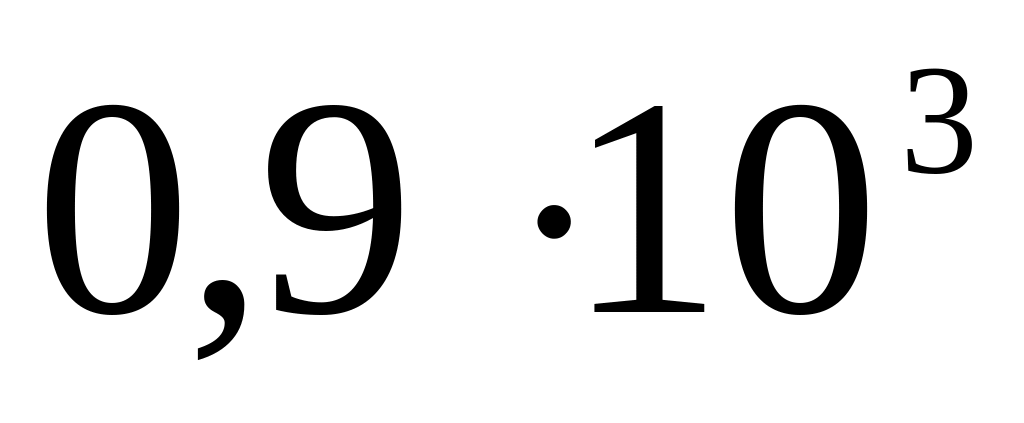 кг/м3.
кг/м3.Сферический кусок льда (с начальным радиусом
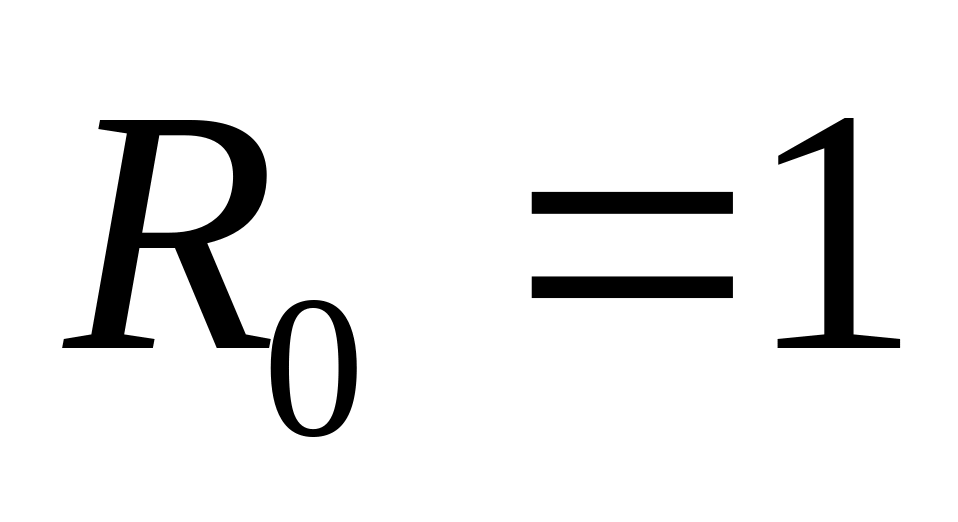 см) погружен в большую массу воды с
температурой 100С.
Предполагая, что теплопередача в
жидкости связана только с ее
теплопроводностью, определить время
,
в течении которого лед полностью
растает. Теплопроводность воды
см) погружен в большую массу воды с
температурой 100С.
Предполагая, что теплопередача в
жидкости связана только с ее
теплопроводностью, определить время
,
в течении которого лед полностью
растает. Теплопроводность воды
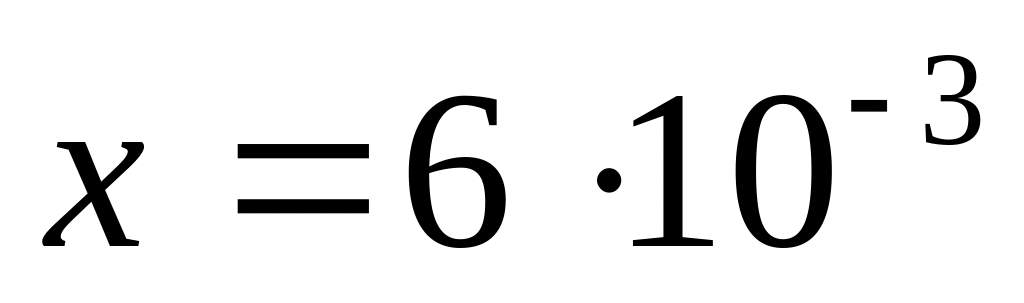 Дж/(с·см·0С),
удельная теплота плавления льда
Дж/(с·см·0С),
удельная теплота плавления льда
 Дж/г.
Дж/г.
РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА И БОЛЬЦМАНА
Цель – понять, что и на какой основе изучает статистическая физика; как выражаются средние по ансамблю значения макроскопических характеристик термодинамических систем.
Указания к самостоятельной работе.
Изучить теоретический материал по конспекту лекций и учебным пособиям [4, стр. 310-324; 2, стр. 107-114]. Обратите внимание на то, в каких условиях статистические закономерности имеют смысл, что такое макросостояния и микросостояния системы, что понимают под статистическим ансамблем и почему усреднения по ансамблю значения макрохарактеристик можно рассматривать как истинные.
Вопросы для экспресс – контроля.
Приведите распределения Максвелла по компонентам импульсов, по величине импульсов.
Приведите распределения Максвелла по компонентам скоростей, по величине скорости.
Обоснуйте основные свойства распределения Максвелла по скоростям. Какова роль молекул хвостовой части распределения?
Как изменяется кривая распределения молекул по скоростям с увеличением температуры?
Что такое наиболее вероятная, средняя и средняя квадратичная скорости и посредством каких математических операций можно получить формулы для их определения из распределения Максвелла?
Какие две тенденции действуют в газе, находящемся во внешнем потенциальном поле?
Приведите распределение Больцмана и поясните его смысл.
В опыте Штерна (см рис.) на поверхности вращающегося цилиндра С конденсируются молекулы серебра с различными скоростями. Каким скоростям молекул, попадающих на пластинку ДД’, соответствует наибольшее почернение?
*
 Найти
относительное число молекул газа,
скорости которых отличаются не более
чем на
Найти
относительное число молекул газа,
скорости которых отличаются не более
чем на
 от значения:
от значения:
наиболее вероятной скорости;
средней квадратичной скорости.
Определить с помощью распределения Максвелла давление, оказываемое газом на стенку, если температура газа и концентрация молекул .
*Газ состоит из молекул массы и находится при температуре . Найти с помощью распределения Максвелла по скоростям соответствующее распределение молекул по кинетическим энергиям
 .
Определить наиболее вероятное значение
кинетической энергии
.
Определить наиболее вероятное значение
кинетической энергии
 .
Соответствует ли
наиболее вероятной скорости?
.
Соответствует ли
наиболее вероятной скорости?*Какая часть молекул газа, находящегося при температуре , имеет кинетическую энергию поступательного движения большую, чем
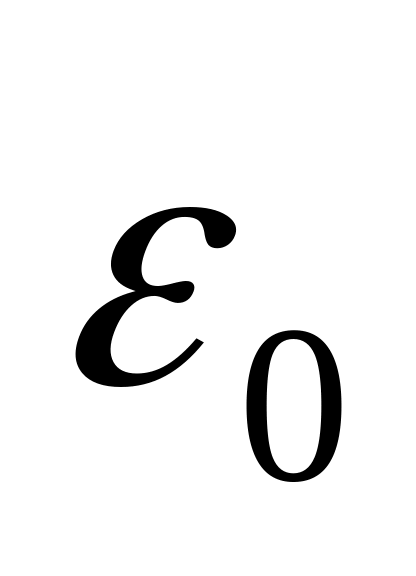 ,
если
,
если
 ?
?Распределение молекул по скоростям в пучке, выходящем из отверстия в сосуде, описывается функцией
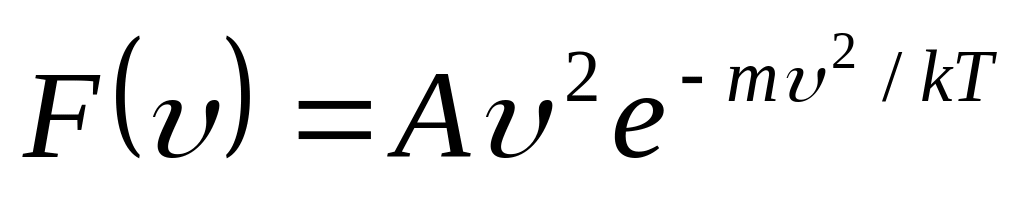 ,
где
– температура газа внутри сосуда.
Найти наиболее вероятные значения:
,
где
– температура газа внутри сосуда.
Найти наиболее вероятные значения:
скорости молекул в пучке; сравнить полученную величину с наиболее вероятной скоростью в самом сосуде;
кинетической энергии молекул в пучке.
При наблюдении в микроскоп взвешенных частиц гуммигута обнаружено, что среднее их число в слоях, расстояние между которыми
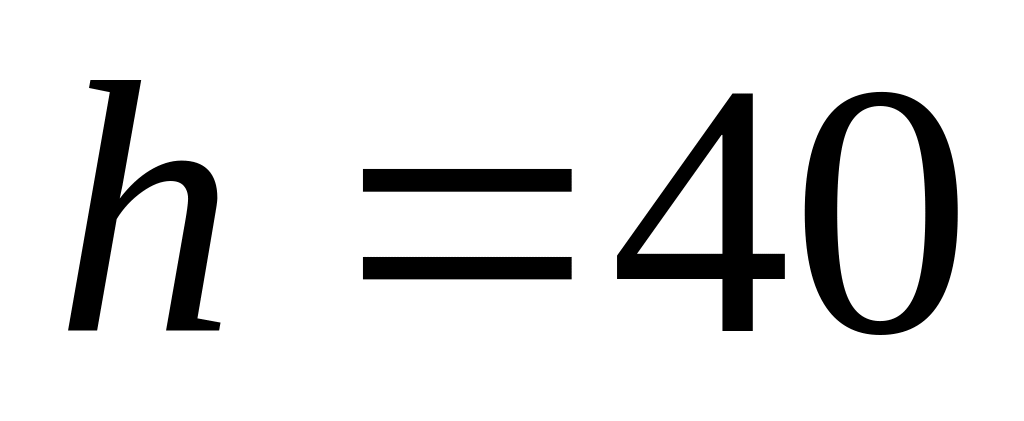 мкм, отличается друг от друга в
мкм, отличается друг от друга в
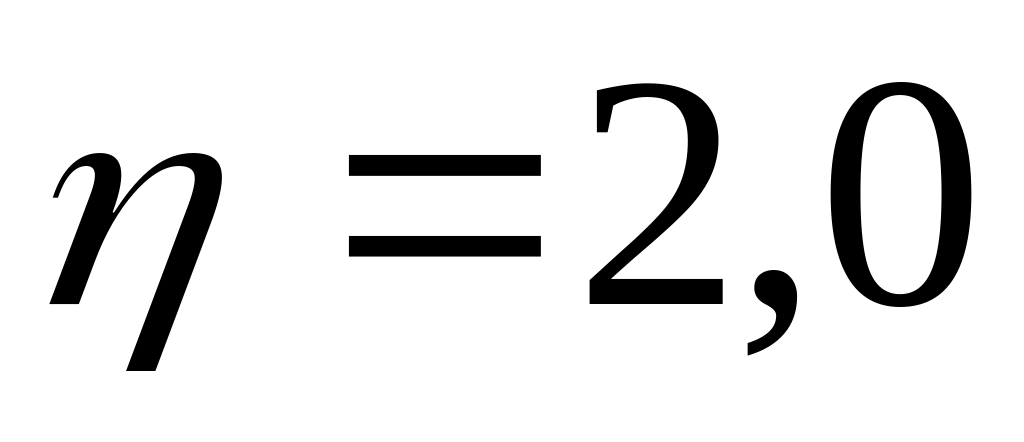 раза. Температура среды
раза. Температура среды
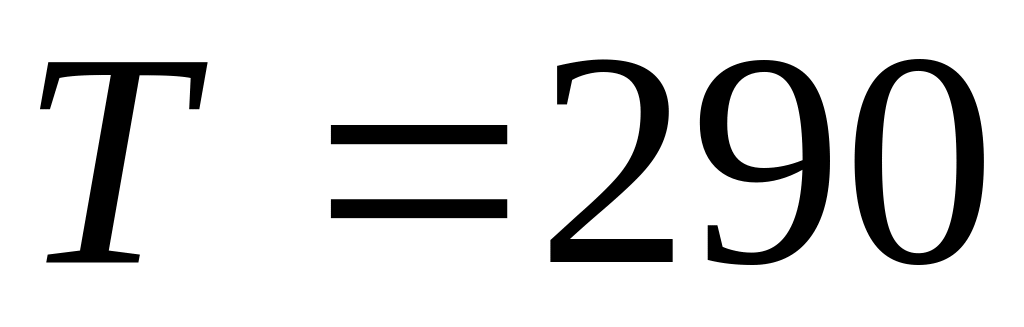 К. Диаметр частиц
К. Диаметр частиц
 мкм и их плотность на
мкм и их плотность на
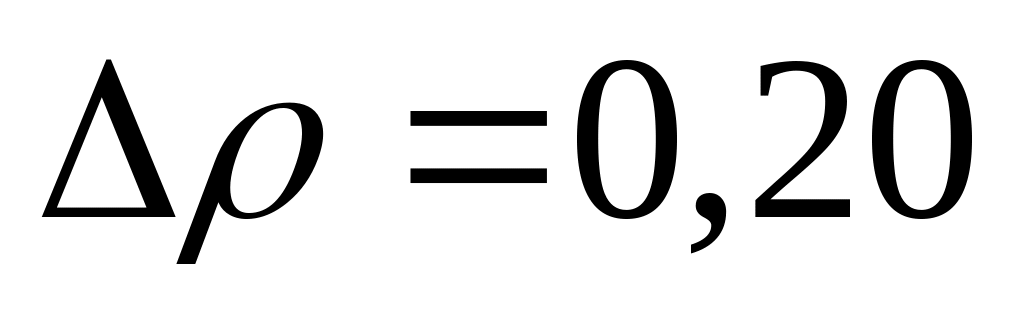 г/см3
больше плотности окружающей жидкости.
Найти по этим данным число Авогадро.
г/см3
больше плотности окружающей жидкости.
Найти по этим данным число Авогадро.*В длинном вертикальном сосуде находится газ, состоящий из двух сортов молекул с массами
 и
и
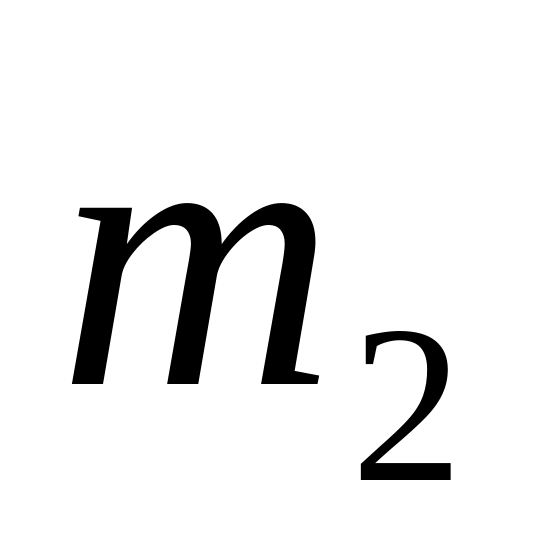 ,
причем
,
причем
 .
Концентрации этих молекул у дна сосуда
равны соответственно
.
Концентрации этих молекул у дна сосуда
равны соответственно
 и
и
 ,
причем
,
причем
 .
Считая, что по всей высоте поддерживается
одна и та же температура
и ускорение свободного падения равно
.
Считая, что по всей высоте поддерживается
одна и та же температура
и ускорение свободного падения равно
 ,
найти высоту
,
найти высоту
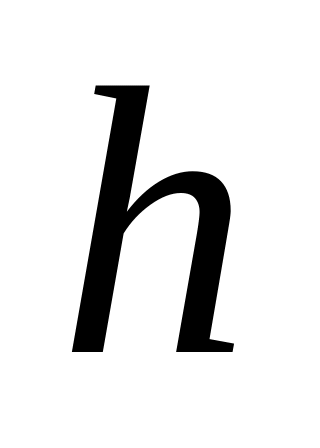 ,
на которой концентрации этих сортов
молекул будут одинаковыми.
,
на которой концентрации этих сортов
молекул будут одинаковыми.*В очень высоком вертикальном цилиндрическом сосуде находится углекислый газ при некоторой температуре . Считая поле тяжести однородным, найти, как изменится давление газа на дно сосуда, если температуру газа увеличить в
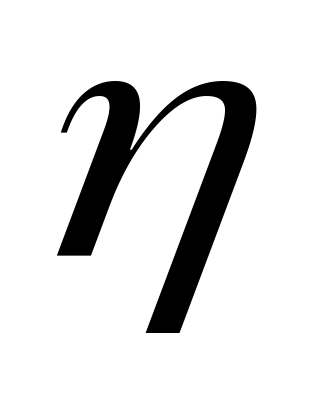 раз.
раз.Горизонтально расположенную трубку с закрытыми торцами вращают с постоянной угловой скоростью
 вокруг вертикальной оси, проходящей
через один из его торцов. В трубке
находится углекислый газ при температуре
Т=3000
К. Длина трубки
вокруг вертикальной оси, проходящей
через один из его торцов. В трубке
находится углекислый газ при температуре
Т=3000
К. Длина трубки
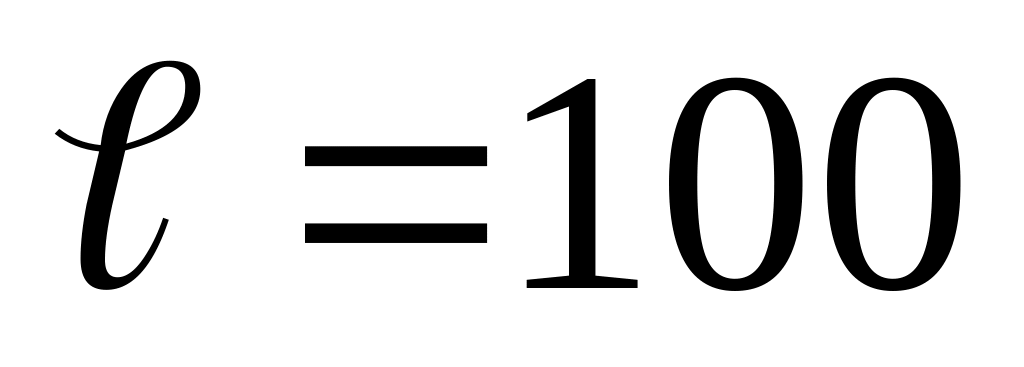 см. Найти значение
,
при котором отношение концентраций
молекул у противоположных торцов
трубки
см. Найти значение
,
при котором отношение концентраций
молекул у противоположных торцов
трубки
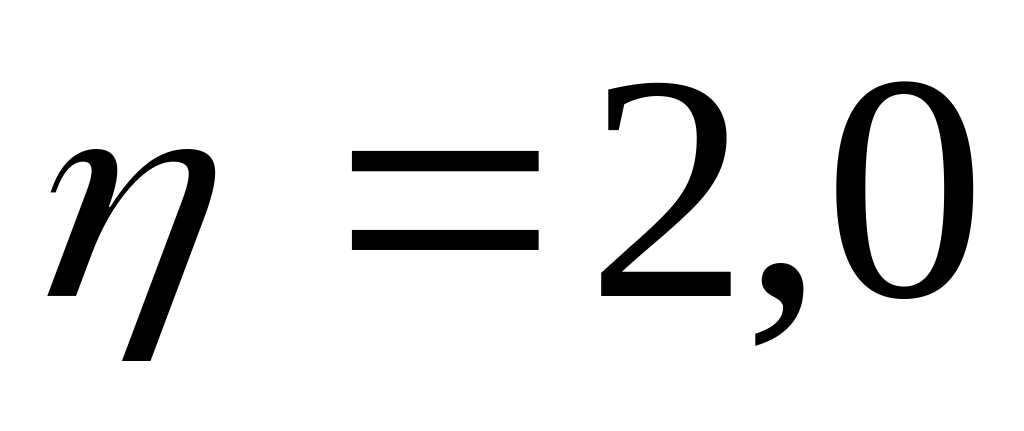 .
.
КВАНТОВЫЕ СТАТИСТИКИ. ПОНЯТИЕ ПЛОТНОСТИ СОСТОЯНИЙ. ЭЛЕКТРОННЫЙ ГАЗ В МЕТАЛЛАХ
Цель – понять, в чем различие статистичности в квантовой механике и в классической статистической физике, научиться применять квантовые статистики Ферми-Дирака и Бозе – Эйнштейна для описания коллективных свойств микрочастиц.
Указания к самостоятельной работе.
Подготовиться к занятию, изучив теоретический материал по конспекту лекций и учебным пособиям [3, стр. 157-165, 179-184; 2, стр. 488-496]. Обратите внимание на то, что по своим коллективным свойствам микрочастицы подразделяются на бозоны и фермионы. Распределение фермионов по квантовым состояниям определяется принципом Паули, в соответствии с которым в одном квантовом состоянии может находиться не более одного фермиона. При этом, квантовая статистика фермионных газов описывается распределением
![]()
и называется статистикой Ферми-Дирака.
В отличие от фермионов, бозоны могут накапливаться в одном состоянии, при этом квантовая статистика бозонов описывается распределением
![]()
и называется статистикой Бозе-Эйнштейна.
