2.6 Решение разностных уравнений с помощью z-преобразований

Пусть линейное разностное уравнение имеет вид:

.

Для решения должны быть заданы значения в первые моменты времени (m-1)

.

Перепишем исходное уравнение относительно z-изображений

,

где - характеристическое уравнение,

- изображение входного сигнала,

- обусловлен начальными условиями.

В общем случае - полином порядка n, коэффициенты которого зависят от начальных условий. При нулевых начальных условиях

,

- определим в результате обратного z-преобразования

1. Для определения можно разложить на простые дроби и воспользоваться таблицами.

2. Если нас не интересует аналитическое выражение , а только конкретные значения при 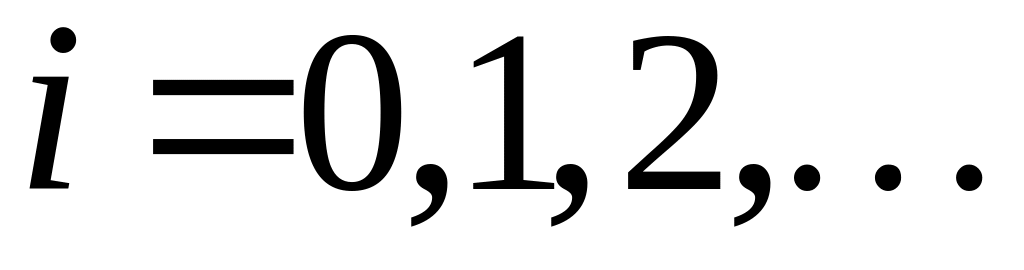, то можно разложить в ряд Лорана по убывающим степеням z.

.

Это следует из определения z-преобразований

.

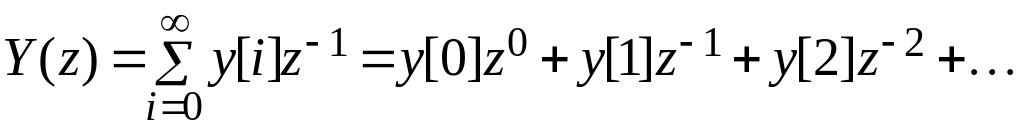Пример. ;

Представим в виде суммы двух дробей

, .

Отсюда , ; .

Тогда .

Значит .

.

.

Пример. Разложим в ряд Лорана.

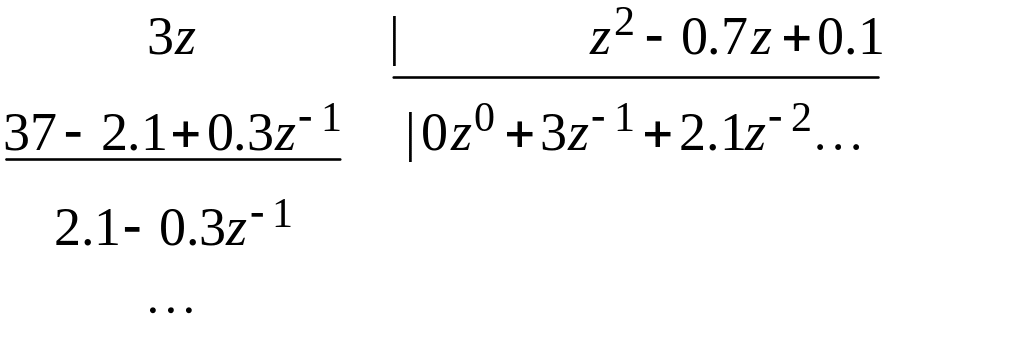
Отсюда .

2.7 Передаточная функция разомкнутой импульсной системы

Импульсная система содержит ИЭ в канале ошибки, рис. 2.2.

Рис. 2.2

ИЭ генерирует решетчатую функцию

.

Задача Э (формирующего элемента) состоит в формировании реального импульса (прямоугольной, треугольной, трапециидальной и т.д. формы).

.

Реакция непрерывной части системы совместно с Э – приведенная весовая функция . Если выходную величину рассматривать только в дискретные моменты времени - .

Реакцией импульсной функции на дискрету является ,

на является ,

на является ,

на является .

Тогда .

Для дискретных моментов времени .

Найдем z-преобразование от левой и правой частей.

На основании теоремы свертки

, где дискретная передаточная функция .

- по аналогии с непрерывными системами: передаточная функция разомкнутой импульсной системы – отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях.

является z-преобразованием весовой функции импульсной системы.

.

Реакцию разомкнутой импульсной системы на входной сигнал произвольной формы можно определить следующим образом:

1. Определить передаточную функцию ПНЧ .

2. Определить соответствующую ей весовую функцию

.

3. Найти весовую функцию импульсной системы .

4. Определить z-изображение .

5. От функции 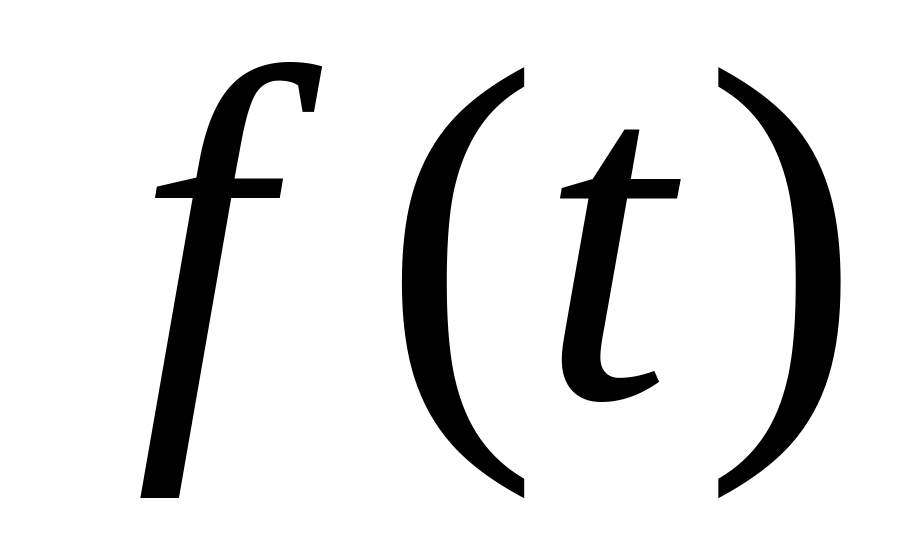перейти к решетчатой функции .

6. Получить изображение .

7. Найти изображение .

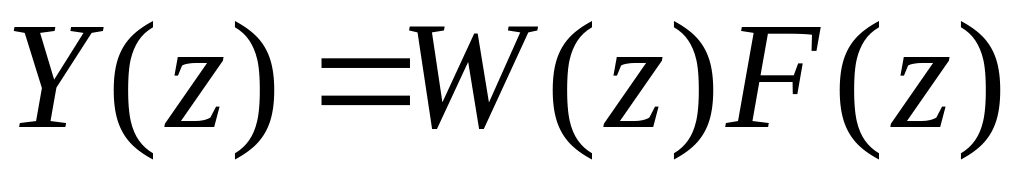8. Найти оригинал .

Соединения звеньев

1. В отличие от непрерывных систем для случая последовательного соединения звеньев с общей передаточной функцией

, ,

где передаточная функция должна определяться по общей весовой функции .

2. Параллельное соединение звеньев

, .

2.8 Характеристики замкнутой импульсной системы

Для опре­деления д.п.ф. замкнутой импульсной системы можно исполь­зовать правила структурных преобразований типовых соеди­нений, сформулированные для непрерывных систем. Но при этом следует помнить, что:

1) обычные правила структурных преобразований справедливы для импульсных систем, лишь если каждая ветвь типового соединения представляет собой типовую импульсную цепь, состоящую из идеального квантователя (на входе цепи) и непрерывной части;

2. при иной структуре цепи и всего типового соединения экви­валентная д.п.ф. определяется более сложными правилами. Для основной схемы одноконтурной импульсной системы д.п.ф. по каналу д-х.

Рис. 2.3

Пусть для системы с единичной обратной связью (рис. 2.3) определена (для общего случая ) передаточная функция разомкнутой системы . Тогда изображение выходной величины

, (2.14)

где - изображение ошибки, так как ИЭ реагирует на значения Х в дискретные моменты времени . При имеем , подставляя его в (2.13), получим:

,

,

,

; (2.15)

,

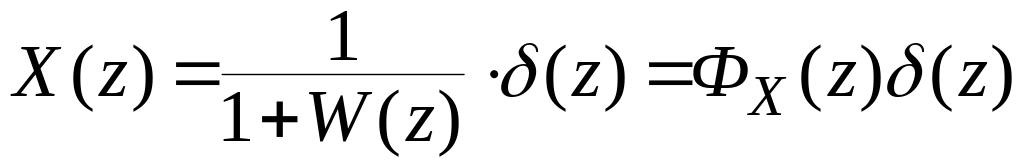(2.16)

где - передаточная функция замкнутой системы,

- передаточная функция замкнутой системы по ошибке.

- д.п.ф. разомкнутого контура, представляющего собой (в данной схеме) типовую импульсную цепь.

Характеристическое уравнение импульсной системы

или в развернутых формах

Характеристическое уравнение:

Условием применимости полученных формул является требование равенства 0 приведенной весовой функции в момент . Для этого в системах с бесконечно короткими импульсами в виде -функций требуется, чтобы степень числителя передаточной функции по крайней мере на два была меньше степени знаменателя.

В системах с конечными по длительности импульсами достаточно чтобы разность была бы не меньше, чем 1.

Передаточные функции – могут быть использованы для оценки устойчивости и качества импульсных систем.

Если , то учитывая, что – изображение ошибки

. Это выражение практически не используется.

Кроме того, .

Для случая неединичной обратной связи, рис. 2.4.

Рис. 2.4

.

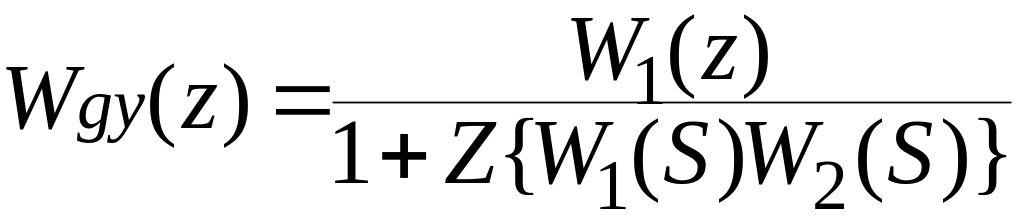Пример. Определим характеристики замкнутой импульсной системы, разомкнутый контур которого соответствует цепи, содержащей «ключ», фиксатор и идеальный интегратор.

Подставляя точную д.п.ф. (2.13) в формулы (2.15) и (2.16), получим соответствующие д.п.ф. замкнутой системы:

; (2.17)

. (2.18)

Характеристическое уравнение системы:

.

Найдем операторное уравнение динамики системы по каналу д-х. Разделив предварительно числитель и знаменатель д.п.ф. (2.18) на z, получим

(2.19)

Уравнению (2.19) соответствует разностное уравнение в рекуррентной форме (при Т=1):