Задача 10.1. Дана задача Коши для системы двух обыкновенных дифференциальных уравнений

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Составить программу-функцию нахождения решения системы ОДУ 1-го порядка по явному методу Эйлера.

2. Численно решить задачу на отрезке [0,1] c шагом h=0.2 явным методом Эйлера.

3. Используя встроенную функцию rkfixed пакета MATHCAD, найти приближенное решение задачи Коши с шагом h=0.2 по методу Рунге-Кутты 4-го порядка точности.

4. На одном чертеже построить графики первой компоненты u(t) найденного обоими методами решения, а на другом - графики второй компоненты v(t) найденного обоими методами решения.

5*. Численно решить ту же задачу с шагом h=0.1 явным методом Эйлера и методом Рунге-Кутты 4-го порядка точности. Используя правило Рунге практической оценки погрешностей, определить погрешность решения, найденного каждым из указанных методов.

10.1.13

Теория:

Явный метод Эйлера.

1. Геометрическая интерпретация метода Эйлера. Простейшим и исторически первым численным методом решения задачи Коши y’(t)=f(t, y(t)), y(t0)=y0 является метод Эйлера. Его можно получить, если в приближенном равенстве оставить только два первых слагаемых (т.е. взять p=1). Тогда формула примет вид

Геометрическая интерпретация одного шага метода Эйлера заключается в аппроксимации решения на отрезке [t , t ] касательной y = y + y’(t )(t – t ), проведённой в точке (t , y ) к интегральной кривой, проходящей через эту точку (см. рисунок).

Таким образом, после выполнения N шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера), для которой угловой коэффициент k очередного n-ого звена равен значению f(t , y ).

Метод Эйлера представляет собой явный одношаговый метод. Для него погрешность аппроксимации имеет вид

2. Устойчивость. Пусть функция f удовлетворяет условию |f’ | < L. Тогда справедливо неравенство

Означающее, что метод Эйлера устойчив на конечном отрезке.

3. Оценка погрешности. Пусть функция f удовлетворяет условию |f’ | < L. Тогда для метода Эйлера справедлива такая оценка глобальной погрешности:

Методы Рунге-Кутты четвёртого порядка точности.

Наиболее известным из методов Рунге-Кутты является классический четырёхэтапный метод четвёртого порядка точности:

Этот метод весьма прост и, как показывает практика, довольно эффективен в обычных расчётах, когда отрезок [t0, T] не очень велик и нужна сравнительно невысокая точность. Также стоит упомянуть, что классический метод Рунге-Кутты четвёртого порядка точности можно рассматривать как аналог формулы Симпсона, отвечающий решению задачи Коши, т.к. применение метода к решению задачи о вычислении интеграла порождает формулу Симпсона

Решение:

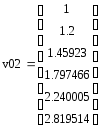
Вводим исходные данные

- формула явного метода Эйлера

- решения полученные явным методом Эйлера с шагом 0.2

- метод Рунге-Кутты 4-ого порядка точности

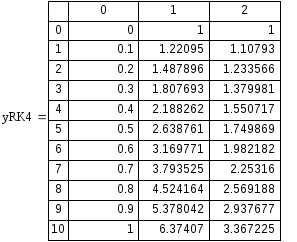
- решения полученные

методом Рунге-Кутты 4-ого порядка точности с шагом 0.2

-графики решений для

u и v полученные методами Рунге-Кутты (RK02) и Эйлера (02) с шагом 0.2

-уменьшаем шаг до 0.1 и повторяем расчёты для этого шага

_{- порядки точности методов (Р-К =4, Эйлера=1)}

Рассчитываем погрешность по правилу Рунге-Кутты для обоих методов:

Эйлера:

Рунге-Кутты:

Получаем погрешности:

явный м. Эйлера: м. Рунге-Кутты 4ого порядка точности:

Задача 10.2. Дана задача Коши для двух систем обыкновенных дифференциальных уравнений с постоянными коэффициентами

,

,

где и – заданные матрицы, - заданные векторы.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Используя встроенную функцию eigenvals(M) (M – матрица) пакета MATHCAD для нахождения собственных чисел матриц A и B, найти коэффициенты жесткости обеих систем. Установить какая задача является жесткой.

2. Составить программу-функцию нахождения решения системы ОДУ 1 порядка с постоянными коэффициентами по явному методу Эйлера.

3. Численно решить обе задачи на отрезке [0,1] c шагом h=0.01 явным методом Эйлера. Определить, для какой из задач явный метод неустойчив при данном шаге h.

4. Составить программу-функцию нахождения решения системы ОДУ 1 порядка с постоянными коэффициентами по неявному методу Эйлера. Используя составленную программу, найти решение жесткой задачи с шагом h=0.01. Построить графики компонент полученного решения.

5. Для жесткой задачи экспериментально подобрать шаг h, при котором графики компонент решения, полученного по явному методу Эйлера, визуально совпадают с графиками компонент решения, полученного по неявному методу с шагом h=0.01. Сравнить найденное значение шага с теоретическим значением шага, при котором явный метод Эйлера для жестких задач должен быть устойчивым.

10.2.13