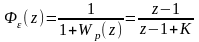Цифровая система, описание которой задается передаточной функцией

,

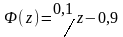будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Система будет устойчива, если все корни характеристического уравнения по модулю меньше единицы. Если хотя бы один корень по модулю больше единицы, то система неустойчива. Равенство единице модуля хотя бы одного корня означает, что система находится на границе устойчивости. При этом, если это корень вещественный, то граница устойчивости относится к нейтральному типу, если корень комплексный, то граница относится к колебательному типу. Особый случай получается, когда вещественный корень системы равен -1. Этот случай условно относят к границе устойчивости нейтрального типа, либо выделяют в особый, третий тип границ устойчивости.

Характеристическое уравнение рассматриваемой системы определяется знаменателем передаточной функции и имеет вид λ - 0,9 = 0. Корень характеристического уравнения равен λ₁ = 0,9. Его модуль меньше единицы, система устойчива.

Правильный ответ: устойчива.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 430.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

устойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа.

!False

на границе устойчивости колебательного типа

!Task 17

Цифровая система, описание которой задается передаточной функцией

,

будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Система будет устойчива, если все корни характеристического уравнения по модулю меньше единицы. Если хотя бы один корень по модулю больше единицы, то система неустойчива. Равенство единице модуля хотя бы одного корня означает, что система находится на границе устойчивости. При этом, если это корень вещественный, то граница устойчивости относится к нейтральному типу, если корень комплексный, то граница относится к колебательному типу. Особый случай получается, когда вещественный корень системы равен -1. Этот случай условно относят к границе устойчивости нейтрального типа, либо выделяют в особый, третий тип границ устойчивости.

Характеристическое уравнение рассматриваемой системы имеет вид λ² – 1,6λ + 0,64 = 0. Корни характеристического уравнения равны

λ_1,2 = 0,8 ±√(0,64-0,64) = 0,8 ±0 ,

или λ₁ = 0,8 , λ₂ = 0,8. Все корни по модулю меньше единицы, система устойчива.

Правильный ответ: устойчива.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 430.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

устойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

на границе устойчивости колебательного типа

!Task 18

Цифровая система с единичной отрицательной обратной связью, описание разомкнутого контура которой задается передаточной функцией

,

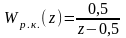будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Система будет устойчива, если все корни характеристического уравнения по модулю меньше единицы. Если хотя бы один корень по модулю больше единицы, то система неустойчива. Равенство единице модуля хотя бы одного корня означает, что система находится на границе устойчивости. При этом, если это корень вещественный, то граница устойчивости относится к нейтральному типу, если корень комплексный, то граница относится к колебательному типу. Особый случай получается, когда вещественный корень системы равен -1. Этот случай условно относят к границе устойчивости нейтрального типа, либо выделяют в особый, третий тип границ устойчивости.

Передаточная функция замкнутой системы определяется по передаточной функции разомкнутого контура

Характеристическое уравнение рассматриваемой системы

определяется знаменателем передаточной функции и имеет вид

λ = 0. Корень характеристического уравнения равен λ₁ = 0. Его модуль меньше единицы, система устойчива.

Правильный ответ: устойчива.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 430.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

устойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

на границе устойчивости колебательного типа

!Task 19

Цифровая система с единичной отрицательной обратной связью, описание разомкнутого контура которой задается передаточной функцией

,

будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Система будет устойчива, если все корни характеристического уравнения по модулю меньше единицы. Если хотя бы один корень по модулю больше единицы, то система неустойчива. Равенство единице модуля хотя бы одного корня означает, что система находится на границе устойчивости. При этом, если это корень вещественный, то граница устойчивости относится к нейтральному типу, если корень комплексный, то граница относится к колебательному типу. Особый случай получается, когда вещественный корень системы равен -1. Этот случай условно относят к границе устойчивости нейтрального типа, либо выделяют в особый, третий тип границ устойчивости.

Передаточная функция замкнутой системы определяется по передаточной функции разомкнутого контура

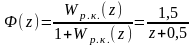
Характеристическое уравнение рассматриваемой системы

определяется знаменателем передаточной функции и имеет вид

λ +0,5 = 0. Корень характеристического уравнения равен λ₁ = -0,5. Его модуль меньше единицы, система устойчива.

Правильный ответ: устойчива.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 430.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

устойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

на границе устойчивости колебательного типа

!END

*********************************************

*ОТУ 1.5.04.t2.rtf

*********************************************

!Taskfile ОТУ 1.5.04.#Основы корневого метода оценки устойчивости

!DE=ОТУ 1.5.#Цифровые системы управления

!Type=2

!Time=2

Экспертные и технологические параметры заданий:

1. Дисциплина: Основы теории управления

2. Объем часов: группа I (от 80 до 170 часов)

3. Дидактическая единица ГОС: Цифровые системы управления

4. Тема задания: Основы корневого метода оценки устойчивости

5. Уровень сложности: 1 (знать и использовать в типовой учебной ситуации)

6. Ориентировочное время выполнения: 2 минуты

7. Перечень контролируемых учебных элементов

Студент должен знать: методику оценки устойчивости цифровой системы по её корням

8. Форма заданий: выбор одного ответа из четырех предложенных

!Task 1

При расположении корней характеристического уравнения на комплексной плоскости, как показано на рисунке,

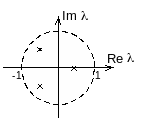
замкнутая система будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Согласно корневому критерию устойчивости, если все корни характеристического уравнения по модулю меньше 1,то система устойчива. Корни системы, показанные на рисунке, располагаются в круге единичного радиуса, т.е. по модулю меньше единицы. Следовательно, система устойчива.

Правильный ответ: устойчивой.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 431.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

устойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа.

!False

на границе устойчивости колебательного типа

!Task 2

При расположении корней характеристического уравнения на комплексной плоскости, как показано на рисунке,

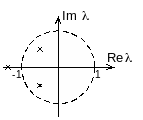
замкнутая система будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Согласно корневому критерию устойчивости, если все корни характеристического уравнения по модулю меньше 1,то система устойчива. Один из корней характеристического уравнения системы, показанных на рисунке, располагается вне круга единичного радиуса, т.е. по модулю он больше единицы. Следовательно, система неустойчива.

Правильный ответ: неустойчива.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 431.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

неустойчива

!False

устойчива

!False

на границе устойчивости нейтрального типа

!False

на границе устойчивости колебательного типа

!Task 3

При расположении корней характеристического уравнения на комплексной плоскости, как показано на рисунке,

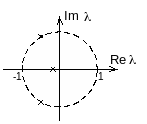
замкнутая система будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Согласно корневому критерию устойчивости, если все корни характеристического уравнения по модулю меньше 1,то система устойчива. Пара комплексно сопряженных корней характеристического уравнения системы, показанные на рисунке, располагаются на окружности единичного радиуса, т.е. по модулю равны единицы. Следовательно, система находится на границе устойчивости колебательного типа.

Правильный ответ: на границе устойчивости колебательного типа.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 431.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

на границе устойчивости колебательного типа

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

устойчива

!Task 4

При расположении корней характеристического уравнения на комплексной плоскости, как показано на рисунке,

замкнутая система будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Согласно корневому критерию устойчивости, если все корни характеристического уравнения по модулю меньше 1,то система устойчива. Вещественный корень характеристического уравнения системы, показанный на рисунке, располагается на окружности единичного радиуса, т.е. равен единице. Следовательно, система находится на границе устойчивости нейтрального типа.

Правильный ответ: на границе устойчивости нейтрального типа.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 431.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

на границе устойчивости нейтрального типа

!False

неустойчивой

!False

на границе устойчивости колебательного типа

!False

устойчивой

!Task 5

Структурная схема системы показана на рисунке, где z^-1 – передаточная функция элемента чистого запаздывания на один такт работы.

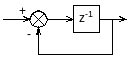
Замкнутая система будет …

!Solution

Устойчивость систем определяется по корням характеристического уравнения. Согласно корневому критерию устойчивости, если все корни характеристического уравнения по модулю меньше 1,то система устойчива. Передаточная функция замкнутой системы равна

Ф(z) = 1/(z+1) .

Вещественный корень характеристического уравнения системы равен - 1. Следовательно, система находится на границе устойчивости .

Правильный ответ: на границе устойчивости.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 431.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

на границе устойчивости

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

устойчива

!Task 6

Исследования устойчивости дискретной системы можно выполнить с применением критерия Гурвица, если к характеристическому уравнению замкнутой системы предварительно применить билинейное преобразование вида …

!Solution

В теории функций комплексного переменного известны преобразования переменных, отображающих круг единичного радиуса в левую полуплоскость плоскости комплексных чисел. Применение таких преобразований позволяет использовать методы исследования устойчивости непрерывных систем в задачах исследования устойчивости дискретных и цифровых систем. Одним из таких преобразований является билинейное преобразование z = ( 1+ω)/(1-ω).

Правильный ответ:

z = ( 1+ω)/(1-ω) . Литература:

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 432.

2. Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

z = ( 1+ω)/(1-ω)

!False

z = ω/(1-ω)

!False

z = 1/(1+ω)

!False

z = (1+ω)

!Task 7

После применения билинейного преобразования z = (1+ω)/(1-ω) к характеристическому уравнению замкнутой цифровой системы получено уравнение

ω² - 0.8ω + 0.6 = 0.

На основании критерия Гурвица можно сказать, что цифровая система управления …

!Solution

В теории функций комплексного переменного известны преобразования переменных, отображающих круг единичного радиуса в левую полуплоскость плоскости комплексных чисел. Применение таких преобразований позволяет использовать методы исследования устойчивости непрерывных систем в задачах исследования устойчивости дискретных и цифровых систем. Одним из таких преобразований является билинейное преобразование z = ( 1+ω)/(1-ω). Характеристическое уравнение замкнутой системы относительно новой переменной имеет один отрицательный коэффициент, что недопустимо для устойчивой системы. Следовательно, цифровая система неустойчива.

Правильный ответ:

неустойчива. Литература:

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 432.

2. Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

неустойчива

!False

неустойчива

!False

на границе устойчивости нейтрального типа

!False

на границе устойчивости колебательного типа

!Task 8

Вещественный положительный корень характеристического уравнения, по модулю меньший единицы, |λ₁|< 1, порождает в переходной составляющей решения разностного уравнения компоненту

,

которая будет …

!Solution

Общее решение неоднородного разностного уравнения, как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т.е. общее решение однородного уравнения, определяется следующим образом:

y(n) = C₁λ₁ⁿ + C₂λ₂ⁿ + ...+ C_mλ_mⁿ,

где λ_i - некратные корни характеристического уравнения, i=1,...,m.

Для вещественного корня, при |λ_i|< 1, соответствующее слагаемое с ростом n будет экспоненциально стремиться к нулю, т.е. экспоненциально затухать.

Правильный ответ:

экспоненциально затухать. Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 410.

!True

экспоненциально затухать

!False

колебательно затухать

!False

экспоненциально возрастать

!False

колебательно возрастать

!Task 9

Вещественный отрицательный корень характеристического уравнения, по модулю меньший единицы, |λ₁|< 1, порождает в переходной составляющей решения разностного уравнения компоненту

,

которая будет …

!Solution

Общее решение неоднородного разностного уравнения, как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т.е. общее решение однородного уравнения, определяется следующим образом:

y(n) = C₁λ₁ⁿ + C₂λ₂ⁿ + ...+ C_mλ_mⁿ,

где λ_i - некратные корни характеристического уравнения, i=1,...,m.

Для вещественного отрицательного корня, при |λ_i|< 1, соответствующее слагаемое с ростом n будет колебательно стремиться к нулю, т.е. колебательно затухать.

Правильный ответ:

колебательно затухать.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 410.

!True

колебательно затухать

!False

экспоненциально затухать

!False

экспоненциально возрастать

!False

колебательно возрастать

!Task 10

Вещественный положительный корень характеристического уравнения, по модулю больше единицы, |λ₁|> 1, порождает в переходной составляющей решения разностного уравнения компоненту

,

которая будет …

!Solution

Общее решение неоднородного разностного уравнения, как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т.е. общее решение однородного уравнения, определяется следующим образом:

y(n) = C₁λ₁ⁿ + C₂λ₂ⁿ + ...+ C_mλ_mⁿ,

где λ_i - некратные корни характеристического уравнения, i=1,...,m.

Для вещественного корня, при |λ_i|> 1, соответствующее слагаемое с ростом n будет экспоненциально возрастать.

Правильный ответ:

экспоненциально возрастать. Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 410.

!True

экспоненциально возрастать

!False

колебательно затухать

!False

экспоненциально затухать

!False

колебательно возрастать

!END

*********************************************

*ОТУ 1.5.05.t2.rtf

*********************************************

!Taskfile ОТУ 1.5.05.#Анализ качества и аналитическое конструирование цифровых регуляторов

!DE=ОТУ 1.5.#Цифровые системы управления

!Type=2

!Time=2

Экспертные и технологические параметры заданий:

1. Дисциплина: Основы теории управления

2. Объем часов: группа I (от 80 до 170 часов)

3. Дидактическая единица ГОС: Цифровые системы управления

4. Тема задания: Анализ качества и аналитическое конструирование цифровых регуляторов

5. Уровень сложности: 2 (знать и уметь использовать в типовой учебной ситуации)

6. Ориентировочное время выполнения: 2 минуты

7. Перечень контролируемых учебных элементов

Студент должен знать: способы анализа показателей качества цифровых систем управления

уметь: производить аналитический синтез регуляторов на основе вектрно-матричных методов (модальное управление)

8. Форма заданий: выбор одного ответа из четырех предложенных

!Task 1

Динамика замкнутой системы описывается разностным уранением

y[(n+1)T] = -0,5 y[nT] + 8 g[nT], y[0] = C₀,

где: T – период квантования времени, n = 0,1, … - дискретное время,

g[*] – входная переменная, y[*] – выходная переменная, C₀ – константа.

Собственное движение замкнутой автономной системы будет …

!Solution

Характер собственного движения автономной системы первого порядка определяется корнем характеристического уравнения, равного

λ = - 0,5 .

Так как корень по модулю меньше единицы и отрицательный, то собственное движение системы носит характер сходящегося к нулю колебательного процесса.

Правильный ответ: сходящимся к нулю, колебательным.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 224.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

!True

сходящимся к нулю, колебательным

!False

сходящимся к нулю, апериодическим

!False

сходящимся к 8, апериодическим

!False

расходящимся

!Task 2

Динамика замкнутой системы описывается разностным уранением

y[(n+1)T] = 0,5 y[nT] + 10 g[nT], y[0] = C₀,

где: T – период квантования времени, n = 0,1, … - дискретное время,

g[*] – входная переменная, y[*] – выходная переменная, C₀ – константа.

Собственное движение замкнутой автономной системы будет …

!Solution

Характер собственного движения автономной системы первого порядка определяется корнем характеристического уравнения, равного

λ = 0,5 .

Так как корень по модулю меньше единицы и положительный, то собственное движение системы носит характер сходящегося к нулю апериодического процесса.

Правильный ответ: сходящимся к нулю, апериодическим.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 224.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

!True

сходящимся к нулю, апериодическим

!False

сходящимся к нулю, колебательным

!False

сходящимся к 10, апериодическим

!False

расходящимся

!Task 3

2 Структурная схема системы c последовательным корректирующим звеном показана на рисунке.

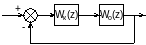
Передаточная функция замкнутой системы по ошибке равна …

!Solution

Правила преобразования структурных схем одинаковые для непрерывных и для дискретных систем управления. Потому передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = 1 / [1 + W_к(z)W_о(z)].

Правильный ответ: 1 / [1 + W_к(z)W_о(z)].

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 426.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

1 / [1 + W_к(z)W_о(z)].

!False

W_к(z)W_o(z) / [1 + W_к(z)W_o(z)].

!False

W_к(z) / [1 + W_к(z)W_o(z)].

!False

1 / W_к(z) W_о(z).

!Task 4

Структурная схема системы c последовательным корректирующим звеном показана на рисунке.

Передаточная функция замкнутой системы по задающему воздействию равна …

!Solution

Правила преобразования структурных схем одинаковые для непрерывных и для дискретных систем управления. Потому передаточная функция замкнутой системы по задающему воздействию равна

Ф(z) = W_к(z)W_о(z) / [1 + W_к(z)W_о(z)].

Правильный ответ: W_к(z)W_о(z) / [1 + W_к(z)W_о(z)].

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 426.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

W_к(z)W_о(z) / [1 + W_к(z)W_о(z)]

!False

1 / [1 + W_к(z)W_o(z)]

!False

W_к(z) / [1 + W_к(z)W_o(z)]

!False

1 / W_к(z) W_о(z)

!Task 5

Динамика замкнутой системы описывается разностным уранением

y[(n+1)T] = 0,8 y[nT] + 10 g[nT], y[0] = 0,

где: T – период квантования времени, n = 0,1, … - дискретное время,

g[*] – входная переменная, y[*] – выходная переменная, C₀ – константа.

Величина перерегулирования при реакции на единичное задающее воздействие у такой системы будет равна _____ %.

!Solution

Характер собственного движения автономной системы первого порядка определяется корнем характеристического уравнения, равного

λ = 0,8 .

Так как корень по модулю меньше единицы и положительный, то собственное движение системы носит характер сходящегося к нулю апериодического процесса. Соответственно, реакция системы на единичное входное воздействие также будет апериодической, т.е. перерегулирование равно 0.

Правильный ответ: 0%.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 437.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

0

!False

10

!False

8

!False

0,8

!Task 6

После подачи на вход системы единичного воздействия g(n) = 1ⁿ, был зафиксирован максимум выходной величины, равный 1.2; установившееся значение выходной величины составило 0.8. Значение перерегулирования равно _____ %.

!Solution

Перерегулированием называется максимальное значение превышения установившегося значения выходной величины системы, вычисленное по переходной характеристике в процентах относительно установившегося значения. Значение перерегулирования вычисляется по формуле

σ% = [(y_max – y())/y()] *100%, где y(n) – переходная характеристика системы. По условию задачи y_max =1.2, y() = 0.8. Следовательно, значение перерегулирования равно

σ% = (1.2-0.8)/0.8*100% = 0.4/0.8 *100% = 50%

Правильный ответ: 50%.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 437.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

50

!False

40

!False

20

!False

10

!Task 7

При снятии переходной характеристики дискретной системы было зафиксировано значение перерегулирования, равное 40%. После уменьшения значения общего коэффициента передачи разомкнутого контура, значение перерегулирования снизилось до 20%. Запас устойчивости системы …

!Solution

Перерегулирование характеризует склонность системы к колебаниям и, как следствие, запас устойчивости. В дискретных системах понятия запаса устойчивости, показателя колебательности и перерегулирования определяются точно также, как и у непрерывных систем. Уменьшение перерегулирования означает снижение склонности системы к колебаниям, следовательно, означает увеличение запаса устойчивости.

Правильный ответ: увеличился.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 438.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

увеличился

!False

уменьшился

!False

не изменился

!False

не связан с величиной перерегулирования

!Task 8

Корни характеристического уравнения замкнутой дискретной системы равны: λ_1,2 = -0.5 ±j0.3, λ₃ = 0.9, где j – мнимая единица. Степень устойчивости системы равна …

!Solution

Степенью устойчивости дискретной системы называется число, равное единице минус модуль максимального по модулю корня характеристического уравнения системы. В данном случае модули корней равны 0,6 и 0,9. Следовательно, степень устойчивости системы равна 1 - 0,9 = 0,1.

Правильный ответ: 0,1.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 438.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

0,1

!False

0,6

!False

0,9

!False

0,3

!Task 9

Корни характеристического уравнения замкнутой дискретной системы чисто мнимые и равны: λ_1,2 = ±j0.3, где j – мнимая единица. Степень устойчивости системы равна …

!Solution

Степенью устойчивости дискретной системы называется число, равное единице минус модуль максимального по модулю корня характеристического уравнения системы. В данном случае модуль корней равен 0,3. Следовательно, степень устойчивости системы равна 1 - 0,3 = 0,7.

Правильный ответ: 0,7.

Литература: Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с., стр. 438.

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 145

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

0,7

!False

0,3

!False

1

!False

0

!Task 10

У системы с единичной отрицательной обратной связью передаточная функция разомкнутого контура равна

W(z) = 3/(10z - 1) .

Значение установившейся ошибки системы при входном воздействии g_о = 12 будет равно …

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При постоянном входном воздействии величиной g₀ установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке

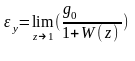
где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = (10z-1)/(10z-1+10) = (z - 0,1)/(z + 0,9).

Корень характеристического уравнения системы равен -0,9 , т.е. замкнутая система устойчивая. Вычисление предела при z→1 при g₀=12 дает значение установившейся ошибки

ε_у = 12*0,9/1,2 = 9.

Правильный ответ: 9

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

9

!False

0,9

!False

0,3

!False

1

!Task 11

Разомкнутый контур системы выполняет функцию цифрового аналога интегратора с передаточной функцией

W(z) = 1/(z - 1) .

Значение установившейся ошибки замкнутой системы с единичной отрицательной обратной связью при входном воздействии g_о = 10 будет равно …

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При постоянном входном воздействии величиной g₀ установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке

где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = (z-1)/(z-1+1) = (z - 1)/z .

Корень характеристического уравнения системы равен 0 , т.е. замкнутая система устойчивая. Вычисление предела при z→1 при g₀=10 дает значение установившейся ошибки

ε_у = 10*0/1 = 0.

Правильный ответ: 0

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

0

!False

1

!False

0,1

!False

10

!Task 12

Разомкнутый контур системы представляется пропорциональным и звеном чистого запаздывания на 1 такт с передаточной функцией

W(z) = 0,8/z .

Значение установившейся ошибки замкнутой системы с единичной отрицательной обратной связью при входном воздействии g_о = 9 будет равно …

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При постоянном входном воздействии величиной g₀ установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке

где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = z/(z +0,8) .

Корень характеристического уравнения системы равен -0.8 , т.е. замкнутая система устойчивая. Вычисление предела при z→1 и g₀=9 дает значение установившейся ошибки

ε_у = 9*1/1,8 = 5.

Правильный ответ: 5

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

5

!False

0

!False

0,8

!False

7,2

!Task 13

Разомкнутый контур системы выполняет функцию цифрового аналога интегратора и описывается передаточной функцией

W(z) = 1/(z - 1) .

На вход замкнутой отрицательной обратной связью системы подано возрастающее входное воздействие g_о (n) = 5n . Учитывая , что Z-преобразование такого сигнала равно G_o(z) = 5z/(z-1)² , значение установившейся ошибки будет равно …

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При произвольном входном воздействии, изображение которого G₀(z), установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке, как

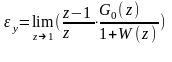
где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = (z-1)/(z-1+1) = (z - 1)/z .

Корень характеристического уравнения системы равен 0 , т.е. замкнутая система устойчивая. Вычисление предела при z→1 дает значение установившейся ошибки

ε_у = (z-1)*5z*(z-1)/z(z-1)²z = 5.

Правильный ответ: 5

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

5

!False

0

!False

1

!False



!Task 14

Разомкнутый контур системы представляется ослабителем и звеном чистого запаздывания на 1 такт с передаточной функцией

W(z) = 0,8/z .

На вход замкнутой отрицательной обратной связью системы подано возрастающее входное воздействие g_о (n) = 8n . Учитывая , что Z-преобразование такого сигнала равно G_o(z) = 8z/(z-1)² , значение установившейся ошибки будет равно …

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При произвольном входном воздействии, изображение которого G₀(z), установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке, как

где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке равна

Ф_ε (z) = z / (z + 0,8) .

Корень характеристического уравнения системы равен - 0,8 , т.е. замкнутая система устойчивая. Вычисление предела при z→1 дает значение установившейся ошибки

ε_у = (z-1)*8z*z / z (z-1)² (z + 0,8) = .

Правильный ответ: 

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True



!False

8

!False

10

!False

0,8

!Task 15

Разомкнутый контур системы выполняет функцию цифрового аналога интегратора и описывается передаточной функцией

W(z) = К/(z - 1) .

На вход замкнутой отрицательной обратной связью системы подано возрастающее входное воздействие g_о (n) = 6n ( Z-преобразование такого сигнала равно G_o(z) = 6z/(z-1)² ). В ходе настройки системы значение коэффициента передачи К увеличили с 1 до 3. Установившаяся ошибка в такой системе

!Solution

Если дискретная система устойчива, то с течением времени переходная составляющая движения стремится к нулю. Ошибка системы определяется входным воздействием и вынужденной составляющей движения системы.

При произвольном входном воздействии, изображение которого G₀(z), установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке, как

где: W(z) - передаточная функция разомкнутой системы.

В данной задаче передаточная функция замкнутой системы по ошибке при К = 3 равна

Ф_ε (z) = (z-1)/(z-1+К) .

Корень характеристического уравнения системы равен 1-К , т.е. при К = 3 замкнутая система неустойчивая. Следовательно, установившаяся ошибка системы ε_у → .

Правильный ответ: → .

Литература:

Душин С.Е., Зотов Н.С., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория автоматического управления: Учебник для вузов/Под ред. В.Б.Яковлева – М.:Высшая школа, 2009 – 579 с., илл., стр. 268

Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.- СПб. Профессия. 2007, 752 с.

Григорьев В.В. и др. Цифровые системы управления: Учебное пособие – СПб.: СПбГУ ИТМО, 2011. – 133 с., илл.

!True

→ 

!False

2

!False

1

!False2

0

!Task 16

Значение коэффициента передачи разомкнутого контура цифровой системы с передаточной функцией

,

при которых система с единичной отрицательной обратной связью будет сохранять свойство устойчивость и обеспечивать минимальную ошибку отработки воздействия G(z) = z/(z-1)², равно (оставить 2 значащие цифры) …

!Solution

Импульсная система устойчива, если все корни ее характеристического уравнения лежат внутри круга единичного радиуса. Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива. Окружность единичного радиуса представляет собой границу устойчивости.

Связь между передаточной функцией разомкнутого контура и замкнутого контура по ошибке дается формулой :

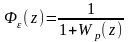
При постоянном входном воздействии величиной g₀ установившаяся ошибка в системе определяется по передаточной функции замкнутой системы по ошибке

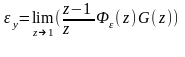
В рассматриваемом случае